辽宁省沈阳市沈河区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-08-05 类型:期末考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 汉字书法博大精深,下列汉字“行”的不同书写字体中,是轴对称图形的是( )A、
 B、
B、 C、
C、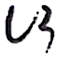 D、
D、 3. 在下列各图的中,正确画出AC边上高的图形是( )A、
3. 在下列各图的中,正确画出AC边上高的图形是( )A、 B、
B、 C、
C、 D、
D、 4. 下列事件中,是必然事件的是( )A、掷一枚质地均匀的硬币,一定正面向上 B、将一滴花生油滴入水中,油会浮在水面上 C、车辆随机到达一个路口,遇到红灯 D、如果a2=b2 , 那么a=b5. 如图,将一张矩形纸片折叠,若 , 则的度数是( )
4. 下列事件中,是必然事件的是( )A、掷一枚质地均匀的硬币,一定正面向上 B、将一滴花生油滴入水中,油会浮在水面上 C、车辆随机到达一个路口,遇到红灯 D、如果a2=b2 , 那么a=b5. 如图,将一张矩形纸片折叠,若 , 则的度数是( ) A、51° B、56° C、61° D、76°6. 下列说法正确的是( )A、相等的角是对顶角 B、在同一平面内,两直线的位置关系有三种:平行,垂直,相交 C、过一点有且只有一条直线与已知直线平行 D、平面内,过一点有且只有一条直线与已知直线垂直7. 如图,在 中,DE是AC的垂直平分线,且分别交BC,AC于D、E两点, , ,则 的度数为( )
A、51° B、56° C、61° D、76°6. 下列说法正确的是( )A、相等的角是对顶角 B、在同一平面内,两直线的位置关系有三种:平行,垂直,相交 C、过一点有且只有一条直线与已知直线平行 D、平面内,过一点有且只有一条直线与已知直线垂直7. 如图,在 中,DE是AC的垂直平分线,且分别交BC,AC于D、E两点, , ,则 的度数为( )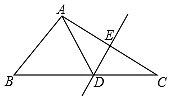 A、 B、 C、 D、8. 一个正方形的边长增加3cm,它的面积就增加 , 这个正方形的边长是( )A、5 B、6 C、8 D、109. 从一定的高度任意抛掷一枚质地均匀的硬币的次数很大时,落下后,正面朝上的频率最有可能接近的数值为( )A、0.83 B、0.52 C、1.50 D、1.0310. 如图,在四边形ABCD中,对角线AC平分∠BAD,AB>AD,下列结论正确的是( )
A、 B、 C、 D、8. 一个正方形的边长增加3cm,它的面积就增加 , 这个正方形的边长是( )A、5 B、6 C、8 D、109. 从一定的高度任意抛掷一枚质地均匀的硬币的次数很大时,落下后,正面朝上的频率最有可能接近的数值为( )A、0.83 B、0.52 C、1.50 D、1.0310. 如图,在四边形ABCD中,对角线AC平分∠BAD,AB>AD,下列结论正确的是( ) A、 B、 C、 D、的大小关系不确定
A、 B、 C、 D、的大小关系不确定二、填空题
-
11. 用科学记数法表示:0.007398= .12. 若a﹣b=1,ab=﹣2,则(a﹣2)(b+2)=.13. 如果一个角的补角是145°,那么这个角的余角的度数是 .14. 比较两个数的大小 . (直接填“>”“<”“=”)15. 已知△ABC是等腰三角形,它的周长为20cm , 一条边长6cm , 那么腰长是 .16. 在中, , , , 点D为直线BC上一动点,以AD为直角边在AD的右侧作等腰 , 使 , , A、E两点间的最小距离为 .

三、解答题
-
17. 计算:(1)、(2)、(利用完全平方公式计算)18.19. 先化简,再求值 , 其中20. 已知:如图, , , .

请说明的理由.
理由:过点C作交AD的延长线于点G,
可得 ▲ (两直线平行,内错角相等)
∵ ,
∴ ▲ ( )
∴ ▲ ( )
∵(已知)
∴ ▲ ( )
∵(已知)
∴ ▲ ( )
∴(等角对等边)
∵ ▲ (已证)
∴(等量代换)
21. 将五张背面图案完全一样的卡片,分别标上数字1,2,3,4,4,洗匀后,背面朝上放在桌面上.请完成下列各题.(1)、随机抽取一张,抽到4的概率;(2)、随机抽取一张,抽出奇数的概率;(3)、若哥哥和弟弟用这五张卡片来玩游戏,哥哥抽出标有偶数的卡片赢,弟弟抽出标有奇数的卡片赢.这个游戏公平吗?如果公平,请说明理由;如果不公平,请修改游戏规则(不改变卡片的数量和内容)使游戏公平.22. 如图,在长度为1个单位长度的小正方形组成的正方形网格中,的三个顶点A、B、C都在格点上. (1)、在图1中画出与关于直线l成轴对称的;(2)、在图1中的直线l上找出一点Q,使得的值最小(保留作图痕迹并标上字母Q)(3)、在图2中的直线l上找出一点P,使得的值最大(保留作图痕迹并标上字母P)(4)、在正方形网格中存在个格点,使得该格点与B、C两点构成以BC为底边的等腰三角形.23. 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.设慢车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
(1)、在图1中画出与关于直线l成轴对称的;(2)、在图1中的直线l上找出一点Q,使得的值最小(保留作图痕迹并标上字母Q)(3)、在图2中的直线l上找出一点P,使得的值最大(保留作图痕迹并标上字母P)(4)、在正方形网格中存在个格点,使得该格点与B、C两点构成以BC为底边的等腰三角形.23. 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.设慢车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系.根据图象进行以下探究: (1)、甲、乙两地之间的距离为千米;(2)、请解释图中点B的实际意义:;(3)、慢车的速度千米/时,快车的速度千米时,快车到达乙地用时小时;(4)、若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.则第二列快车比第一列快车晚出发小时.24. 如图1,在中, , , , 于点D,且 .
(1)、甲、乙两地之间的距离为千米;(2)、请解释图中点B的实际意义:;(3)、慢车的速度千米/时,快车的速度千米时,快车到达乙地用时小时;(4)、若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.则第二列快车比第一列快车晚出发小时.24. 如图1,在中, , , , 于点D,且 . (1)、若E,F分别是AB,AC上的点,且 , 求证:;(2)、当点F,E分别从C,A两点同时出发,以每秒1个单位长度的速度沿CA,AB运动,到点A,B时停止.设F点运动的时间为x秒,的面积为(用含有x的代数式表示);设的面积为y,则y与x的关系式为;(3)、如图2,在(2)的条件下,点F,E分别沿CA,AB的延长线继续运动,直接写出此时y与x的关系式.25. 经过 顶点 的一条直线, . 分别是直线 上两点,且 .
(1)、若E,F分别是AB,AC上的点,且 , 求证:;(2)、当点F,E分别从C,A两点同时出发,以每秒1个单位长度的速度沿CA,AB运动,到点A,B时停止.设F点运动的时间为x秒,的面积为(用含有x的代数式表示);设的面积为y,则y与x的关系式为;(3)、如图2,在(2)的条件下,点F,E分别沿CA,AB的延长线继续运动,直接写出此时y与x的关系式.25. 经过 顶点 的一条直线, . 分别是直线 上两点,且 . (1)、若直线 经过 的内部,且 在射线 上,请解决下面两个问题:
(1)、若直线 经过 的内部,且 在射线 上,请解决下面两个问题:①如图1,若 , ,则 ; (填“ ”,“ ”或“ ”);
②如图2,若 ,请添加一个关于 与 关系的条件 , 使①中的两个结论仍然成立,并证明两个结论成立.
(2)、如图3,若直线 经过 的外部, ,请提出 三条线段数量关系的合理猜想(不要求证明).