辽宁省锦州市2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-08-05 类型：期末考试

进入出卷网下载

一、单选题

1. 习近平总书记说：“生态环境保护就是为民造福的百年大计”．以下节水、节能、回收、绿色食品的标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 事件“掷一枚质地均匀的硬币，硬币落下后，正面朝上”是（）

A、必然事件 B、确定事件 C、随机事件 D、不可能事件

查看试题解析
3. 下列各式计算正确的是（）

A、 $a^{2} \cdot a^{4} = a^{8}$ B、 ${(a^{2} b)}^{3} \div a b = a^{5} b^{2}$ C、 $a^{6} \div a^{3} = a^{2}$ D、 ${(y^{2})}^{3} = y^{5}$

查看试题解析
4. 如图，下列说法错误的是（）

A、 $∠ 2$ 与 $∠ 6$ 是同位角 B、 $∠ 3$ 与 $∠ 4$ 是内错角 C、 $∠ 1$ 与 $∠ 3$ 是对顶角 D、 $∠ 3$ 与 $∠ 5$ 是同旁内角

查看试题解析
5. 如图，一块三角形的玻璃碎成3块（图中所标1、2、3），小华带第3块碎片去玻璃店，购买形状相同、大小相等的新玻璃，这是利用三角形全等中的（）

A、SAS B、ASA C、AAS D、SAS

查看试题解析
6. 若等腰三角形的两边长分别是3和6，则这个三角形的周长是（）

A、12 B、15 C、12或15 D、9

查看试题解析
7. 计算 $2^{2021} \times {(- \frac{1}{2})}^{2022}$ 的结果是（）

A、2 B、-2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
8. 如图，① $∠ 1 = ∠ 3$ ， ② $∠ 2 = ∠ 3$ ， ③ $∠ 1 = ∠ 4$ ， ④ $∠ 2 + ∠ 5 = 180 °$ 可以判定 $b ∥ c$ 的条件有（）．

A、①②④ B、①②③ C、②③④ D、①②③④

查看试题解析
9. 如图1，在边长为a的大正方形中，剪去一个边长为3的小正方形，将余下的部分按图中的虚线剪开后，拼成如图2所示的长方形，根据两个图形阴影部分面积相等的关系，可验证的等式为（）

A、 $(a - 3)^{2} = a^{2} - 6 a + 9$ B、 $(a + 3)^{2} = a^{2} + 6 a + 9$ C、 $a (a + 3) = a^{2} + 3 a$ D、 $(a + 3) (a - 3) = a^{2} - 9$

查看试题解析
10. 一段笔直的公路AC长20千米，途中有一处休息点B，AB长15千米，甲、乙两名长跑爱好者同时从点A出发，甲以15千米/时的速度匀速跑至点B，原地休息半小时后，再以10千米/时的速度匀速跑至终点C；乙以12千米/时的速度匀速跑至终点C，下列选项中，能符合题意反映甲、乙两人出发后2小时内运动路程y（千米）与时间x（小时）函数关系的图象是（　　）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 一个不透明的袋子里有3个红球和5个白球，每个球除颜色外都相同，从袋中任意摸出一个球，那么摸到红球的可能性比摸到白球的可能性．（填“大”“小”或“相同”）

查看试题解析
12. 生物具有遗传多样性，遗传信息大多储存在DNA分子上，一个DNA分子的直径约为 $0.00000021 c m$ ．这个数量用科学记数法可表示为 $c m$ ．

查看试题解析
13. 某校九（2）班在体育考试中全班所有学生的得分情况如表所示：
分数段（分）
15～19
20～24
25～29
30
人数
1
5
9
25
从九（2）班的学生中随机抽取一人，恰好是获得30分的学生的概率是.

查看试题解析
14. 如图，在灌溉时，要把河中的水引到农田P处，农民李伯伯的做法是：过点P作 $P M$ 垂直于河岸l，垂足为M，沿 $P M$ 开挖水渠距离最短，其中的数学原理是．

查看试题解析
15. 如图，点D，E分别在线段 $B C$ ， $A C$ 上，连接 $A D$ ， $B E$ ．若 $∠ A = 35 °$ ， $∠ B = 25 °$ ， $∠ C = 50 °$ ，则 $∠ 1$ 的大小为．

查看试题解析
16. 小涵用100元钱去买单价是8元的笔记本，则她剩余的钱数Q（元）与她买这种笔记本的本数x（本）之间的关系式是．

查看试题解析
17. 如图，将 $△ A B C$ 沿 $A C$ 所在的直线翻折得到 $△ A B^{^{'}} C$ ，再将 $△ A B^{^{'}} C$ 沿 $A B^{'}$ 所在的直线翻折得到 $△ A B^{'} C^{'}$ ，若点 $B ， B^{'} ， C^{'}$ 在同一条直线上， $∠ B A C = α$ ．有下列结论：① $△ A B^{'} C^{'} ≌ △ A B C$ ， ② $B B^{'} ⊥ A C$ ， ③ $∠ C B^{'} B = 2 α$ ，其中正确的说法是．（填序号即可）

查看试题解析
18. 如图， $C A ⊥ A B$ 于点A， $A B = 4 ， A C = 2$ ，射线 $B M ⊥ A B$ 于点B，一动点D从点A出发以2个单位/秒的速度沿射线 $A B$ 运动，E为射线 $B M$ 上一动点，随着点D的运动而运动，且始终保持 $E D = B C$ ，若点D运动t秒 $(t > 0)$ ， $△ E D B$ 与 $△ B C A$ 全等，则t的值为．

查看试题解析

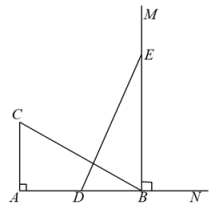
三、解答题

19. 计算：

(1)、 $2 {(x^{2})}^{3} + x (x - 2 x^{5})$ ；

(2)、 $(2022 - 2005)^{0} + {(\frac{1}{3})}^{- 2} - | - 6 |$ ．

查看试题解析
20. 先化简，再求值： $[(x + 2 y) (x - 2 y) - (x - 2 y)^{2}] \div 4 y$ ，其中 $x = 2$ ， $y = \frac{1}{2}$ ．

查看试题解析
21. 请在下列括号内填上相应步骤或理由．
已知：如图， $A B ∥ C D ， A D ⊥ A C$ ，垂足为A， $∠ 1 = ∠ 2$ ．
试说明： $E F ⊥ A C$ ．
解：因为 $A B ∥ C D$ （已知），
所以 $∠ 1 = ∠ D$ （   ）．
因为 $∠ 1 = ∠ 2$ （已知），
所以 $∠ 2 =$   ▲  （等量代换）．
所以 $E F ∥ A D$ （    ）．
所以 $∠ C E F = ∠ C A D$ （   ）．
因为 $A D ⊥ A C$ （已知），
所以 $∠ C A D = 90 °$ （垂直的定义）．
所以 $∠ C E F = 90 °$ （    ）．
所以 $E F ⊥ A C$ （垂直的定义）．

查看试题解析
22. 如图是一个材质均匀的转盘，转盘被分成8个全等的扇形，颜色分为红、绿、黄三种，指针的位置固定，转动转盘后任其自由停止（若指针指向两个扇形的交线时，当作指向右边的扇形），转动一次转盘．

(1)、求指针指向绿色扇形的概率；

(2)、指针指向红色扇形的概率大，还是绿色扇形的概率大？为什么？（要求（1）、（2）题写出解答过程）

查看试题解析
23. 已知小明家、超市、体育场依次在同一条直线上，超市离家 $3 k m$ ，体育场离家 $5 k m$ ，小明从家出发，匀速骑行 $0.2 h$ 到达超市；在超市停留 $0.2 h$ 后，匀速骑行 $0.1 h$ 到达体育场；在体育场锻炼一段时间后，匀速骑行回到家．下面给出的图像反映了这个过程中小明离家的距离与离开家的时间之间的对应关系．请根据相关信息解答下列问题：

(1)、依据题中提供的信息将下列表格补充完整：

离开家的时间/h

0.1

0.3

1

1.8

离家的距离/ $k m$

5

(2)、依据题中提供的信息填空：
①小明从超市骑行到体育场的速度为 $k m / h$ ；

②当小明离家的距离为 $2 k m$ 时，他离开家的时间为．

查看试题解析
24. 【发现规律】
善于思考的小聪对“十位数字相同，个位数字的和为10的两位数乘法”进行了深入地探究，得到了下列速算方法：十位数字相同，个位数字的和为10的两位数相乘，将一个因数的十位数字与另一个因数的十位数字加1的和相乘，所得的积作为计算结果的前两位；将两个因数的个位数字之积作为计算结果的后两位（若数位不足两位，则用零补齐）．比如 $47 \times 43$ ，它们乘积的前两位是4与 $(4 + 1)$ 的积，即20，它们乘积的后两位是7与3的积，即21，所以 $47 \times 43 = 2021$ ；又如 $21 \times 29 ， 2 \times (2 + 1) = 6$ ，不足两位，就将6写在百位， $1 \times 9 = 9$ ，不足两位，就将9写在个位，十位上写零，所以 $21 \times 29 = 609$ ．

(1)、【应用规律】
请用上述阅读材料的方法计算： $74 \times 76 =$ ；

(2)、请你写出一个具有类似结构特征的两位数乘法：；

(3)、【证明规律】
设其中一个因数的十位数字为a，个位数字为b（ $1 \leq a \leq 9 ， 1 \leq b \leq 9$ ；a，b都是正整数），
①则这两个因数分别表示为 ▲ 和 ▲ ；（用含a，b的代数式表示）
②用所学的整式的乘法说明上述阅读材料中的速算方法是正确的．

查看试题解析
25. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 ° ， A C = 6 ， A B = 10$ ．

(1)、用尺规按下列要求作图：（不写作法和结论，保留清晰的作图痕迹）
①作 $△ A B C$ 的角平分线 $A D$ ；
②作线段 $A D$ 的垂直平分线 $E F$ ，交 $A D$ 于点G；

(2)、连接 $C G$ ，若 $△ A C G$ 的面积为4.5，
求：①点D到直线 $A B$ 的距离；
② $R t △ A B C$ 的面积．
（如果（1）问完成有困难，可根据备用图完成此问的作答）

查看试题解析
26. 如图1，在 $△ A B C$ 中， $A B = A C$ ， D是 $B C$ 的中点，过点B作 $B E ⊥ A C$ ，垂足为E，连接 $A D$ 交 $B E$ 于点F．

(1)、猜想 $∠ C B E$ 与 $∠ C A D$ 的数量关系，并说明理由；

(2)、P是射线 $E B$ 上的点，过点C作 $C G$ // $E B$ 交 $P D$ 的延长线于点G．
①如图2，若点P在 $E B$ 的延长线上，请说明 $P E = B E + C G$ 的理由；
②若 $B E = 3 ， C G = 1.5$ ，则 $P E =$ ▲ ．

查看试题解析

分数段（分）	15～19	20～24	25～29	30
人数	1	5	9	25

离开家的时间/h	0.1	0.3	1	1.8
离家的距离/ $k m$			5