辽宁省本溪市2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-08-05 类型:期末考试
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 北京2022年冬奥会会徽(冬梦),是第24届冬季奥林匹克运动会使用的标志,主要由会徽图形、文字标志、奥林匹克五环标志组成,组成会徽的四个图案中是轴对称图形的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下面四个图形中,∠1和∠2一定相等的是( )A、
3. 下面四个图形中,∠1和∠2一定相等的是( )A、 B、
B、 C、
C、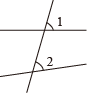 D、
D、 4. 小明掷一枚质地均匀的硬币,掷前9次时共有6次正面朝上,那么他掷第10次时,出现正面朝上的概率是( )A、1 B、 C、 D、05. 甲以每小时5km的速度行走,他所走的路程S(km)与行走时间t(h)之间的关系式为 , 其中自变量是( )A、S B、5 C、t D、S和t6. 在一个三角形中,有两个内角度数是40°和50°,则这个三角形是( )A、锐角三角形 B、钝角三角形 C、等腰三角形 D、直角三角形7. 如图,和中, , , 若 , 则等于( )
4. 小明掷一枚质地均匀的硬币,掷前9次时共有6次正面朝上,那么他掷第10次时,出现正面朝上的概率是( )A、1 B、 C、 D、05. 甲以每小时5km的速度行走,他所走的路程S(km)与行走时间t(h)之间的关系式为 , 其中自变量是( )A、S B、5 C、t D、S和t6. 在一个三角形中,有两个内角度数是40°和50°,则这个三角形是( )A、锐角三角形 B、钝角三角形 C、等腰三角形 D、直角三角形7. 如图,和中, , , 若 , 则等于( ) A、10° B、20° C、30° D、40°8. 如图,直线// , 直角三角板ABC的直角顶点C在直线b上,若 , 则度数为( )
A、10° B、20° C、30° D、40°8. 如图,直线// , 直角三角板ABC的直角顶点C在直线b上,若 , 则度数为( )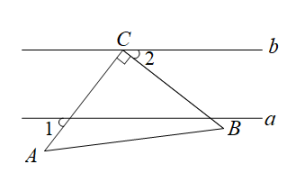 A、25° B、35° C、45° D、55°9. 在如图所示的网格中,是格点三角形(即顶点恰好是网格线的交点),则与有一条公共边且全等(不含)的所有格点三角形的个数是( )
A、25° B、35° C、45° D、55°9. 在如图所示的网格中,是格点三角形(即顶点恰好是网格线的交点),则与有一条公共边且全等(不含)的所有格点三角形的个数是( ) A、4个 B、3个 C、2个 D、1个10. 如图①,在长方形ABCD中, , , 动点P从点B出发,沿着折线B→A→D→C方向匀速运动到点C停止运动,在整个运动过程中,设点P运动的路程为x,的面积为y,如果y关于x的关系图象如图②所示,那么线段BC的长为( )
A、4个 B、3个 C、2个 D、1个10. 如图①,在长方形ABCD中, , , 动点P从点B出发,沿着折线B→A→D→C方向匀速运动到点C停止运动,在整个运动过程中,设点P运动的路程为x,的面积为y,如果y关于x的关系图象如图②所示,那么线段BC的长为( ) A、10 B、7 C、4 D、3
A、10 B、7 C、4 D、3二、填空题
-
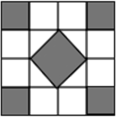
11. 石墨烯是现在世界上最薄的纳米材料,其理论厚度仅有0.00000000034米,将数据0.00000000034用科学记数法表示为 .12. 一个不透明口袋中有红球、白球共10个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一球,记下它的颜色后再放回口袋中,不断重复这一过程.通过大量重复摸球试验后发现,摸到白球的频率稳定在0.7,那么口袋中白球的个数很可能是个.13. 如果一个角的补角是115°,那么这个角的余角的度数是 .14. 一个小球在如图所示的方格地板上自由滚动,并随机停留在某块地板上,每块地板大小、质地完全相同,那么该小球停留在黑色区域的概率是 .
 15. 若 , , 则 .16. 若 , 则 .17. 已知直线 , 垂足为O,OE在内部, , 于点O,则度.18. 如图,在中, , 过点C作于点D,过点B作于点M,连接MD,过点D作 , 交BM于点N,CD与BM交于点E.下列结论:①;②;③;④ . 其中正确结论有 . (填写序号即可)
15. 若 , , 则 .16. 若 , 则 .17. 已知直线 , 垂足为O,OE在内部, , 于点O,则度.18. 如图,在中, , 过点C作于点D,过点B作于点M,连接MD,过点D作 , 交BM于点N,CD与BM交于点E.下列结论:①;②;③;④ . 其中正确结论有 . (填写序号即可)
三、解答题
-
19.(1)、;(2)、;(3)、;(4)、 .20. 先化简,再求值: , 其中 .21. 下面是小明完成“过直线外一点作这条直线的平行线”的尺规作图.

已知:直线l及直线l外一点P.
求作:直线PQ,使得// . (不写作法,保留作图痕迹)
如图,直线PQ就是所求直线.
(1)、根据作图痕迹,填空:①AC是的 ▲ , ② ▲ ;
(2)、根据作图痕迹,说明直线PQ与l为什么平行?22. 如图,现有一个可以自由转动的转盘(转盘被等分成6个扇形),每个扇形区域内分别标有3,4,5,6,7,8这六个数字,转动转盘,当转盘停止转动后,指针指向的数字即为转出的数字,请回答下列问题: (1)、转出的数字是1是 , 转出的数字是7是;(从“随机事件”,“必然事件”,“不可能事件”中选一个填空)(2)、转动转盘,转出的数字大于7的概率是 .(3)、现有两张分别写有2和3的卡片,随机转动转盘,转盘停止转动后,记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.这三条线段能构成三角形的概率是 .23. 如图,中,AD平分 , 点P为线段AD上的一点,过点P作交直线BC于点E.当 , 时,求的度数.
(1)、转出的数字是1是 , 转出的数字是7是;(从“随机事件”,“必然事件”,“不可能事件”中选一个填空)(2)、转动转盘,转出的数字大于7的概率是 .(3)、现有两张分别写有2和3的卡片,随机转动转盘,转盘停止转动后,记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.这三条线段能构成三角形的概率是 .23. 如图,中,AD平分 , 点P为线段AD上的一点,过点P作交直线BC于点E.当 , 时,求的度数. 24. 小明由甲地骑自行车前往乙地游玩,1小时后,小刚骑摩托车沿相同路线也从甲地前往乙地.在这个过程中,小明和小刚两人离开甲地的距离S(千米)与小明骑车的时间t(小时)之间的关系如图所示,请根据图象回答:
24. 小明由甲地骑自行车前往乙地游玩,1小时后,小刚骑摩托车沿相同路线也从甲地前往乙地.在这个过程中,小明和小刚两人离开甲地的距离S(千米)与小明骑车的时间t(小时)之间的关系如图所示,请根据图象回答: (1)、小明骑自行车的速度是千米/小时,甲乙两地之间的路程为千米;(2)、求小刚骑摩托车的速度是多少千米/时?(3)、图中 , ;(4)、小刚出发后,在到达乙地前,小刚骑摩托车用小时与小明相距10千米.25. 中, , 射线AP平分 , 射线AP交边BC于点D,点H是线段AD延长线上一点,过点H在射线AP上方,作 , 且 .
(1)、小明骑自行车的速度是千米/小时,甲乙两地之间的路程为千米;(2)、求小刚骑摩托车的速度是多少千米/时?(3)、图中 , ;(4)、小刚出发后,在到达乙地前,小刚骑摩托车用小时与小明相距10千米.25. 中, , 射线AP平分 , 射线AP交边BC于点D,点H是线段AD延长线上一点,过点H在射线AP上方,作 , 且 .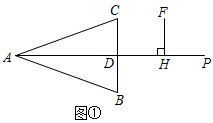

 (1)、如图①,请直接写出线段FH与BD的数量关系;(2)、如图②,连接BF交射线AP于点G,请判断线段BG与FG的数量关系,并说明理由;(3)、过点F作//交射线AP于点E,当 , 时,请直接写出的面积.
(1)、如图①,请直接写出线段FH与BD的数量关系;(2)、如图②,连接BF交射线AP于点G,请判断线段BG与FG的数量关系,并说明理由;(3)、过点F作//交射线AP于点E,当 , 时,请直接写出的面积.