2021-2022学年苏科版数学八年级上册1.3.5探索三角形全等的条件作图同步训练

试卷更新日期：2022-08-05 类型：同步测试

进入出卷网下载

一、单选题

1. 如图，用直尺和圆规作ΔABC和ΔDBC，则ΔABC≌ΔDBC，理由是（）

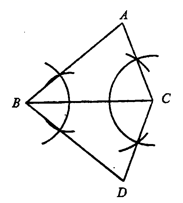A、SAS B、ASA C、AAS D、SSS

查看试题解析
2. 如图，已知锐角∠AOB．在射线OA上取一点C，以点O为圆心，OC的长为半径作弧，交射线OB于点D，连结CD；分别以点C，D为圆心，CD的长为半径作弧，两弧在∠AOB内部交于点P，连结CP，DP；作射线OP，交CD于点Q．根据以上作图过程及所作图形，有下列结论①CP//OB；②∠AOP = ∠BOP；③OP⊥CD．其中正确的结论（）

A、①②③ B、②③ C、①③ D、③

查看试题解析
3. 如图，用尺规作图“过点C作CN//OA”的实质就是作∠DOM=∠NCE，其作图依据是（）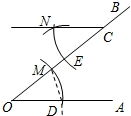

A、SAS B、SSS C、ASA D、AAS

查看试题解析
4. 如图， $△ A B C$ 的面积是30cm² ，以顶点A为圆心，适当长为半径画弧，分别交AC、AB于点M、N，再分别以点M、N为圆心，大于 $\frac{1}{2} M N$ 的长为半径画弧，两弧交于点P，作射线AP，过点C作 $C D ⊥ A P$ 于点D，连接BD，则 $△ D A B$ 的面积是（）

A、15cm² B、14cm² C、13cm² D、12cm²

查看试题解析
5. 如图，在 $△ A B C$ 中 $A B = A C$ ， $∠ B = ∠ A C D = 45 °$ ，D，E是BC上两点，且 $∠ D A E = 45 °$ ，过点A作 $A F ⊥ A D$ ，垂足是A，过点C作 $C F ⊥ B C$ ，垂足是C，CF交AF于点F，连接EF.给出下列结论：① $△ A B D ≌ △ A C F$ ；② $D E = E F$ ；③若 $S_{△ A D E} = 10$ ， $S_{△ C E F} = 4$ ，则 $S_{△ A B C} = 24$ ；④ $B D + C E = D E$ .其中正确结论的字号是（）

A、①②③ B、②③④ C、①③④ D、①②④

查看试题解析
6. 小举在探究全等三角形判定方法，已知如图， $△$ ABC，他通过尺规作图、裁剪、重合的操作，证实一种判定方法．以下是小举的操作过程：
第一步：尺规作图．
作法：（1）作射线 $B ˊ$ M；（2）以点B为圆心，任意长为半径画弧，分别交BA，BC于点E，D；（3）以点 $B ˊ$ 为圆心，BD长为半径画弧，交 $B ˊ$ M于点P；（4）以点P为圆心，DE长为半径画弧，在 $B ˊ$ M的上方交（3）中所画弧于点Q；（5）过点Q作射线BˊN；（6）以点 $B ˊ$ 为圆心，BC长为半径画弧，交 $B ˊ$ M于点 $C ˊ$ ；（7）以点 $B ˊ$ 为圆心，BA长为半径画弧，交 $B ˊ$ N于点 $A ˊ$ ；（8）连接 $A C$ ．
第二步：把作出的 $△ A B C$ 剪下来，放到 $△ A B C$ 上．
第三步：观察发现 $△ A B C$ 和 $△ A B C$ 重合．
∴ $△ A B C ≌ △ A B C$ ．
根据小举的操作过程可知，小举是在探究（）

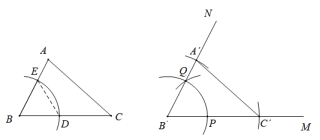A、基本事实SSS B、基本事实ASA C、基本事实SAS D、定理AAS

查看试题解析

二、填空题

7. 如图，在△ABC中，点E在AB上，D为AC的中点，过点C作CF∥AB交ED的延长线于点F.若AB＝15cm，CF＝10cm，则BE＝cm.

查看试题解析
8. 如图，D为等腰Rt△ABC的斜边AB的中点，E为BC边上一点，连接ED并延长交CA的延长线于点F，过D作DH⊥EF交AC于G，交BC的延长线于H，则以下结论：①BE=CG；②DF=DH；③BH=CF；④AF=CH．其中正确的是.

查看试题解析
9. 如图，以△ABC的顶点A为圆心，以BC长为半径作弧；再以顶点C为圆心，以AB长为半径作弧，两弧交于点D；连结AD、CD．若∠B=65°，则∠ADC的大小为度．

查看试题解析
10. 如图， $△ A B C$ 的面积为 $15 c m^{2}$ ，以顶点 $A$ 为圆心，适当长为半径画弧，分别交 $A C$ ， $A B$ 于点 $M$ ， $N$ ，再分别以点 $M$ ， $N$ 为圆心，大于 $\frac{1}{2} M N$ 的长为半径画弧，两弧交于点 $P$ ，作射线 $A P$ ，过点 $C$ 作 $C D ⊥ A P$ 于点 $D$ ，连接 $D B$ ，则 $△ D A B$ 的面积是 $c m^{2}$ ．

查看试题解析
11. 如图，在 $△ A B C$ 和 $△ D B C$ 中， $∠ A = 40 °$ ， $A B = A C = 2$ ， $∠ B D C = 140 °$ ， $B D = C D$ ，以点 $D$ 为顶点作 $∠ M D N = 70 °$ ，两边分别交 $A B$ ， $A C$ 于点 $M$ ， $N$ ，连接 $M N$ ，则 $△ A M N$ 的周长为．

查看试题解析
12. 如图， $△ A B C$ 中， $A B = B C$ ，点D在线段 $B C$ 上（不与点 $B ， C$ 重合）．

作法如下：

①连接 $A D$ ，作 $A D$ 的垂直平分线分别交直线 $A B ， A C$ 于点 $P ， Q$ ，连接 $D P ， D Q$ ，则 $△ A P Q ≌ △ D P Q$ ；

②过点D作 $A C$ 的平行线交 $A B$ 于点P ，在线段 $A C$ 上截取 $A Q$ ，使 $A Q = D P$ ，连接 $P Q ， D Q$ ，则 $△ A P Q ≌ △ D Q P$ ；

③过点D作 $A C$ 的平行线交 $A B$ 于点P ，过点D作 $A B$ 的平行线交 $A C$ 于点Q ，连接 $P Q$ ，则 $△ A P Q ≌ △ D Q P$ ；

④过点D作 $A B$ 的平行线交 $A C$ 于点Q ，在直线 $A B$ 上取一点P ，连接 $D P$ ，使 $D P = A Q$ ，连接 $P Q$ ，则 $△ A P Q ≌ △ D P Q$ ．以上说法一定成立的是．（填写正确的序号）

查看试题解析

三、解答题

13. 如图，点 $A ， E ， F ， C$ 在同一直线上， $A E = C F$ ，过点 $E ， F$ 分别作 $E D ⊥ A C$ ， $F B ⊥ A C$ ， $A B = C D$ ．若 $B D$ 与 $E F$ 交于点G，试证明 $B D$ 平分 $E F$ ；

查看试题解析
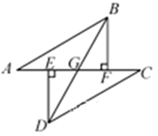14. 如图，在等腰直角三角形ABC中，∠ACB＝90°，点M是边AB上任意一点，连接CM，过点A，B分别作AE⊥CM，BF⊥CM，垂足分别为E，F，若BF＝2.6cm，AE＝0.9cm，分别求出CF，EF的长.

查看试题解析
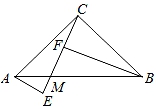15. 在△ABC中，AB=AC，点D是直线BC上一点(不与B，C重合)，以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连结CE。

(1)、如图1，当点D在线段BC上时，如果∠BAC=90°，则∠BCE=。

(2)、设∠BAC=α，∠BCE=β
①如图2，当点D在线段BC上移动时，α，β之间有怎样的数量关系？请说明理由。

②当点D在直线BC上移动时，α，β之间有怎样的数量关系？请你在备用图上画出图形，并直接写出结论。

查看试题解析
16. 在 $Δ A B C$ 中， $A B = A C$ ，点 $D$ 是直线 $B C$ 上一点（不与 $B$ ， $C$ 重合），以 $A D$ 为一边在 $A D$ 的右侧作 $Δ A D E$ ，使 $A D = A E$ ， $∠ D A E = ∠ B A C$ ，连接 $C E$ ．

(1)、如图1，当点 $D$ 在线段 $B C$ 上，如果 $∠ B A C = 90 °$ ，则 $∠ B C E =$ 度；

(2)、如图2，如果 $∠ B A C = 60 °$ ，求 $∠ B C E$ 的度数是多少？

(3)、设 $∠ B A C = α$ ， $∠ B C E = β$ ．
①如图3，当点 $D$ 在线段 $B C$ 上移动，则 $α$ ， $β$ 之间有怎样的数量关系？请说明理由；

②当点 $D$ 在直线 $B C$ 上移动，请直接写出 $α$ ， $β$ 之样的数量关系，不用证明．

查看试题解析