2021-2022学年苏科版数学八年级上册1.3.4探索三角形全等的条件SSS同步训练
试卷更新日期：2022-08-05 类型：同步测试
一、单选题
-
1. 如图是一个平分角的仪器，其中 ， ． 将点A放在一个角的顶点，AB和AD沿着这个角的两边放下，利用全等三角形的性质就能说明射线AC是这个角的平分线，这里判定ABC和ADC是全等三角形的依据是（ ）
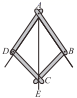A、SSS B、ASA C、SAS D、AAS2. 将三根木条钉成一个三角形木架，这个三角形木架具有稳定性.解释这个现象的数学原理是（ ）A、SSS B、SAS C、ASA D、AAS3. 如图，在△ACE和△BDF中，AE＝BF，CE＝DF，要利用“SSS”证△ACE≌△BDF时，需添加一个条件是（ ）
A、AB＝BC B、DC＝BC C、AB＝CD D、以上都不对4. 如图， ， ，则下列结论中，不正确的是（ ）
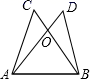A、 B、 C、 D、5. 如图，在△ACD和△BCE中，AC＝BC ， AD＝BE ， CD＝CE ， ∠ACE＝55°，∠BCD＝155°，AD与BE相交于点P ， 则∠BPD的度数为（ ）
A、110° B、125° C、130° D、155°6. 两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形， 其中AD＝CD，AB＝CB，在探究筝形的性质时，得到如下结论：①△ABD≌△CBD；②AC⊥BD；③点O到四条边的距离都相等，④AO＝OC.其中正确的结论有（ ）个.
A、4 B、3 C、2 D、1二、填空题
-
7. 如图，在四边形ABCD中， ， ，E是AC上的点，则图中共有对全等三角形.
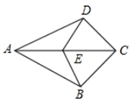
8. 如图，点A，D，B，E在同一条直线上，AD＝BE，AC＝EF，要使△ABC≌△EDF，只需添加一个条件，这个条件可以是 ．
9. 如图，在 ABC和 DEC中，AB＝DE，AC＝DC，CE＝CB.点E在AB上，若∠ACE＝2∠ECB＝50°，则∠D＝.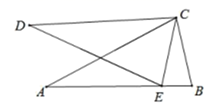
10. 如图，已知AB=AC，EB=EC，AE的延长线交BC于D，则图中全等的三角形共有对.
11. 在正方形网格中，的位置如图所示，则点中在的平分线上是点．
12. 如图，小敏做了一个角平分仪 ，其中 ， ，将仪器上的点A与 的顶点R重合，调整 和 ，使它们分别落在角的两边上，过点A，C画一条射线 ， 就是 的平分线，小敏根据角平分仪的画图原理得到以下结论：① ，② ，③
④ ，则正确的结论有.（填序号）
三、解答题
-
13. 如图，点B、C、D、F在一条直线上，FD＝BC，DE＝CA，EF＝AB，求证：EF∥AB．
14. 已知：如图点A、B、C在同一直线上，且AM＝AN，BM＝BN，求证：CM＝CN．
15. 如图，在△ABC与△ADE中，AB＝AD，AC＝AE，BC＝DE，点D在BC边上．
(1)、求证：∠B＝∠ADE；(2)、直接写出∠1与∠2的数量关系．16. （教材呈现）数学课上，赵老师用无刻度的直尺和圆规按照华师版教材八年级上册87页完成角平分线的作法，方法如下：如图， 为已知角，试按下列步骤用直尺和圆规准确地作出 的平分线.
第一步：在射线OA、OB上，分别截取OD、OE，使
第二步：分别以点D和点E为圆心，适当长（大于线段DE长的一半）为半径作圆弧，在 内，两弧交于点C；
第三步：作射线OC.射线OC就是所要求作的 的平分线
(1)、赵老师用尺规作角平分线时，用到的三角形全等的判定方法是 ．(2)、小明发现只利用直角三角板也可以作 的角平分线，方法如下：步骤：①利用三角板上的刻度，在OA、OB上分别截取OM、ON，使 ．
②分别过点M、N作OM、ON的垂线，交于点P．
③作射线OP，则OP为 的平分线．
请根据小明的作法，求证OP为 的平分线．
