湖南省衡阳市祁东县2021-2022学年高一下学期数学期末考试试卷

试卷更新日期：2022-08-04 类型：期末考试

进入出卷网下载

一、单选题

1. 复数 $z = (9 - 7 i) i$ 在复平面内对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 记 $△ A B C$ 的内角A、B、C的对边分别为a、 $b$ 、c，若 $c o s C = \frac{\sqrt{13}}{4}$ ， $2 a = 3 c$ ，则 $s i n A =$ （）

A、 $\frac{\sqrt{3}}{4}$ B、 $\frac{3 \sqrt{3}}{8}$ C、 $\frac{2 \sqrt{3}}{9}$ D、 $\frac{\sqrt{3}}{9}$

查看试题解析
3. 已知某圆柱的高为5，底面半径为 $\sqrt{3}$ ，则该圆柱的体积为（）

A、6π B、9π C、12π D、15π

查看试题解析
4. 如图，在 $7 \times 5$ 正方形网格中，向量 $\vec{a}$ ， $\vec{b}$ 满足 $\vec{a} ⊥ \vec{b}$ ，则 $\vec{A B} - \vec{A D} + \vec{B C} =$ （）

A、 $2 \vec{a} + \frac{3}{2} \vec{b}$ B、 $- 2 \vec{a} - \frac{3}{2} \vec{b}$ C、 $- 3 \vec{a} + \frac{1}{2} \vec{b}$ D、 $3 \vec{a} - \frac{1}{2} \vec{b}$

查看试题解析
5. 分别投掷两枚质地均匀的骰子，设事件A=“两枚骰子的点数都是奇数”，事件B=“两枚骰子的点数都是偶数”，事件C=“两枚骰子点数之和为奇数”，则事件 $A ∪ B$ 与事件C（）

A、不互斥 B、互斥但不对立 C、互为对立 D、以上说法都不对

查看试题解析
6. 一组数据按从小到大的顺序排列为56，59，60，62，a，若这组数据的极差为7，则这组数据的方差为（）

A、30 B、6 C、25 D、5

查看试题解析
7. 甲、乙两位同学暑假计划从吉林省去河北省旅游，他们所搭乘动车的“3+2”座位车厢如图所示，若这两位同学买到了同一排的座位，则他们的座位正好相邻的概率为（）

A、 $\frac{3}{5}$ B、 $\frac{1}{2}$ C、 $\frac{2}{5}$ D、 $\frac{3}{10}$

查看试题解析
8. 灯笼起源于中国的西汉时期，两千多年来，每逢春节人们便会挂起象征美好团圆意义的红灯笼，营造一种喜庆的氛围．如图1，某球形灯笼的轮廓由三部分组成，上下两部分是两个相同的圆柱的侧面，中间是球面的一部分（除去两个球冠）．如图2，球冠是由球面被一个平面截得的，垂直于截面的直径被截得的部分叫做球冠的高，若球冠所在球的半径为R，球冠的高为h，则球冠的面积 $S = 2 π R h$ ．已知该灯笼的高为46cm，圆柱的高为3cm，圆柱的底面圆直径为30cm，则围成该灯笼所需布料的面积为（）

A、 $2090 π c m^{2}$ B、 $2180 π c m^{2}$ C、 $2340 π c m^{2}$ D、 $2430 π c m^{2}$

查看试题解析

二、多选题

9. 如图，四边形ABCD的斜二测直观图为等腰梯形 $A^{'} B^{'} C^{'} D$ ，已知 $A^{'} B^{'} = 2 C^{'} D^{'} = 4$ ，则（）

A、 $A^{'} D^{'} = \sqrt{2}$ B、 $B C = 2 \sqrt{2}$ C、四边形ABCD的周长为 $6 + 2 \sqrt{2} + 2 \sqrt{3}$ D、四边形ABCD的面积为6 $\sqrt{2}$

查看试题解析
10. 已知复数 $z_{1} = a + i ， z_{2} = 2 + b i ， a ， b \in R$ ，且 $z_{1} + z_{2}$ 为纯虚数， $z_{1} z_{2} < 0$ ，则（）

A、 $a = - 2$ B、 $b = 2$ C、 $| 2 z_{1} - z_{2} | = 37$ D、 $z_{1} + 2 z_{2}$ 的共扼复数为 $2 - 3 i$

查看试题解析
11. 从参加安全知识竞赛的学生中随机抽出40名学生，将其成绩（均为整数）整理后画出的频率分布直方图如图所示．已知65分以下的学生共16人，则下列说法正确的是（）

A、 $a = 0.015$ B、这40名学生的平均成绩约为66分 C、根据此频率分布直方图可计算出这40名学生成绩的中位数约为70分 D、根据此频率分布直方图可计算出这40名学生成绩的上四分位数约为77分

查看试题解析
12. 如图，在棱长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，E是棱 $A_{1} D_{1}$ 的中点，过 $C_{1} E$ 作正方体的截面 $α$ 交棱 $A A_{1}$ 于F，则（）

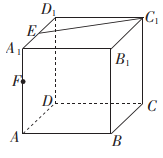A、当 $A_{1} F = 1$ 时，截面为等腰梯形 B、当 $1 < A_{1} F < 2$ 时，截面为六边形 C、当 $A_{1} F = 2$ 时，截面面积为2 $\sqrt{6}$ D、当 $A_{1} F = \frac{3}{2}$ 时，截面 $α$ 与平面 $B C C_{1} B_{1}$ 所成的锐二面角的正切值为 $\frac{2 \sqrt{13}}{3}$

查看试题解析

三、填空题

13. $\frac{1 + i}{2 - 3 i} =$ ．

查看试题解析
14. 驾照考试一共有四个科目：科目一（驾驶员理论考试）、科目二（场地驾驶技能考试）、科目三（道路驾驶技能考试）、科目四（安全文明驾驶常识考试）．只有四个科目都通过才能取得驾照．若某学员四个科目通过的概率依次是0.9、0.8、0.8、0.9，且每个科目是否通过相互之间没有影响，则该学员拿到驾照的概率为．

查看试题解析
15. 剪纸艺术是一种中国传统的民间工艺，它源远流长，经久不衰，已成为世界艺术宝库中的一种珍藏．某学校为了丰富学生的课外活动，组织了剪纸比赛，小明同学在观看了2022年北京冬奥会的节目《雪花》之后，被舞台上一片片漂亮的“雪花”所吸引，决定用作品“雪花”参加剪纸比赛．小明的参赛作品“雪花”如图1所示，它的平面图可简化为图2的平面图形，该平面图形既是轴对称图形，又是中心对称图形，其中， $P$ 为该平面图形上的一个动点（含边界），六边形 $A B C D E F$ 为正六边形， $D C = 4 C K = 4 J K = 8$ ， $C K ⊥ J K$ ， $△ H I J$ 为等边三角形，则 $\vec{A B} \cdot \vec{A P}$ 的最大值为．

查看试题解析
16. 记 $△ A B C$ 的内角A，B，C的对边分别为a，b，c，若 $2 b c o s A = a s i n B$ ，且 $b = 2 ， c = \sqrt{5}$ ，则 $s i n A =$ ， BC边上的高为．

查看试题解析

四、解答题

17. 已知点A（2，-1），B（3，1），C（1，-2）．

(1)、求向量 $\vec{A B}$ 与 $\vec{A C}$ 夹角的余弦值：

(2)、若向量 $\vec{A B} ⊥ (\vec{A B} + t \vec{A C} ）$ ，求实数t的值．

查看试题解析
18. 如图，在四棱锥 $P - A B C D$ 中，底面ABCD是正方形，△PAB为正三角形，且平面PAB⊥底面ABCD， $A D = 2$ ， O为AC与BD的交点．

(1)、求四棱锥P—ABCD的体积；

(2)、证明 $C D ⊥ P O$ ．

查看试题解析
19. 记 $△ A B C$ 的内角 $A$ 、 $B$ 、 $C$ 的对边分别为 $a$ 、 $b$ 、 $c$ ，已知____.
在① $2 c o s 2 C - 8 c o s (A + B) + 5 = 0$ ， ② $s i n^{2} A + s i n^{2} B + s i n A s i n B = s i n^{2} C$ 这两个条件中任选一个，补充在上面的横线上，并解答下列问题.

(1)、求C的大小；

(2)、若 $△ A B C$ 的面积为 $\sqrt{3}$ ，且 $c = \sqrt{14}$ ，求 $△ A B C$ 的周长.

查看试题解析
20. 某农户从一批待售的苹果中随机抽取100个，对样本中每个苹果称重，数据如下表．
质量（单位：千克）
$[0.08 ， 0.09)$
$[0.09 ， 0.1)$
$[0.1 ， 0.11)$
$[0.11 ， 0.12)$
$[0.12 ， 0.13)$
$[0.13 ， 0.14]$
个数
10
10
20
40
15
5
若将这批苹果按质量大小进行分级，质量不小于0.12千克的苹果为一级果；质量不小于0.1千克且小于0.12千克的苹果为二级果；质量在0.1千克以下的苹果为三级果．

(1)、从样本中按等级进行分层抽样，随机抽取5个苹果放入袋子，现采用不放回方式从袋子中依次随机取出2个苹果，求第二次取到二级果的概率．

(2)、若将这批苹果按等级出售，一级果的售价为10元/千克；二级果的售价为8元/千克；三级果的售价为6元/千克．经估算，这批苹果有150000个，求该批苹果的销售收入约为多少元．（同一组中的数据用该组区间的中点值作代表）

查看试题解析
21. 如图，四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的底面ABCD为正方形，O为BD的中点， $A_{1} O$ ⊥底ABCD， $A A_{1} = 2 A B = 4$ ．

(1)、求证：平面 $A_{1} B D$ ∥平面 $C D_{1} B_{1}$ ．

(2)、求直线 $A_{1} B$ 与平面 $B D D_{1} B_{1}$ 所成角的正弦值．

查看试题解析
22. 甲，乙两人进行围棋比赛，采取积分制，规则如下：每胜1局得1分，负1局或平局都不得分，积分先达到2分者获胜；若第四局结束，没有人积分达到2分，则积分多的一方获胜；若第四周结束，没有人积分达到2分，且积分相等，则比赛最终打平．假设在每局比赛中，甲胜的概率为 $\frac{1}{2}$ ，负的概率为 $\frac{1}{3}$ ，且每局比赛之间的胜负相互独立．

(1)、求第三局结束时乙获胜的概率；

(2)、求甲获胜的概率．

查看试题解析

质量（单位：千克）	$[0.08 ， 0.09)$	$[0.09 ， 0.1)$	$[0.1 ， 0.11)$	$[0.11 ， 0.12)$	$[0.12 ， 0.13)$	$[0.13 ， 0.14]$
个数	10	10	20	40	15	5