湖南省郴州市2021-2022学年高一下学期数学期末考试试卷

试卷更新日期：2022-08-04 类型：期末考试

进入出卷网下载

一、单选题

1. 已知 $z = 2 - 3 i$ ，则 $\bar{z}$ 的虚部为（）

A、3i B、 $- 3 i$ C、3 D、-3

查看试题解析
2. 某次数学竞赛中有甲、乙、丙三个方阵，其人数之比为2∶3∶5．现用比例分配的分层随机抽样方法抽取一个容量为50的样本，其中方阵乙被抽取的人数为（）

A、10 B、15 C、20 D、25

查看试题解析
3. 底面半径为2，母线长为4的圆锥的表面积为（）

A、 $\sqrt{6} π$ B、12π C、 $2 \sqrt{3} π$ D、 $2 \sqrt{6} π$

查看试题解析
4. 若向量 $\vec{a} = (1 ， x) ， \vec{b} = (1 - x ， 2)$ ，且 $\vec{a} ⊥ (\vec{a} - \vec{b})$ ，则 $x$ 的值为（）

A、-1 B、0 C、1 D、0或1

查看试题解析
5. △ABC中，内角A、B、C所对的边分别为a、b、c，若 $a = 1$ ， $b = \frac{1}{2}$ ， $c o s A = \frac{\sqrt{3}}{2}$ ，则 $s i n C =$ （）

A、 $\frac{1}{4}$ B、 $\frac{\sqrt{15}}{8}$ C、 $\frac{3}{4}$ D、 $\frac{\sqrt{15} + \sqrt{3}}{8}$

查看试题解析
6. 在正方体ABCD−A₁B₁C₁D₁中，M为棱CC₁的中点，则异面直线AM与C₁D₁所成角的正切值为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{\sqrt{5}}{2}$ D、 $\frac{\sqrt{7}}{2}$

查看试题解析
7. 《周易》是我国古代典籍，用“卦”描述了天地世间万象变化．如图是一个八卦图，包含乾、坤、震、巽、坎、离、兑八卦，每一卦由三根线组成（表示一根阳线，表示一根阴线），现有1人随机的从八卦中任取两卦，六根线中恰有四根阳线和两根阴线的概率为（）

A、 $\frac{1}{14}$ B、 $\frac{3}{28}$ C、 $\frac{3}{14}$ D、 $\frac{7}{28}$

查看试题解析
8. 如图，在△ABC中，点D是线段BC上的动点（端点除外），且 $\vec{A D} = x \vec{A B} + y \vec{A C}$ ，则 $\frac{9}{x} + \frac{1}{y}$ 的最小值为（）

A、16 B、17 C、18 D、19

查看试题解析

二、多选题

9. 下列命题不正确的是（）

A、三点确定一个平面 B、两条相交直线确定一个平面 C、一条直线和一点确定一个平面 D、两条平行直线确定一个平面

查看试题解析
10. 若复数z满足 $z (1 - i) = | 1 - \sqrt{3} i |$ ，则（）

A、 $z = - 1 + i$ B、z的实部为1 C、 $\bar{z} = 1 + i$ D、 $z^{2} = 2 i$

查看试题解析
11. 在 $△ A B C$ 中， $a$ 、 $b$ 、 $c$ 分别为角 $A$ 、 $B$ 、 $C$ 的对边，已知 $\frac{c o s B}{c o s C} = \frac{b}{2 a - c}$ ， $S_{△ A B C} = \frac{\sqrt{3}}{4}$ ，且 $b = \sqrt{2}$ ，则（）

A、 $c o s B = \frac{1}{2}$ B、 $s i n B = \frac{1}{2}$ C、 $a c = 1$ D、 $a + c = \sqrt{5}$

查看试题解析
12. 如图，在正方体ABCD−A₁B₁C₁D₁中，点P在线段BC₁上运动时，下列命题正确的是（）

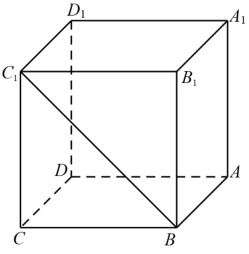A、三棱锥A−D₁PC的体积不变 B、直线CP与直线AD₁的所成角的取值范围为 $[\frac{π}{4} ， \frac{π}{2}]$ C、直线AP与平面ACD₁所成角的大小不变 D、二面角P−AD₁−C的大小不变

查看试题解析

三、填空题

13. 一组数1、2、4、5、6、6、7、8、9的75%分位数为．

查看试题解析
14. 已知事件A、B互斥，且事件A发生的概率P（A）＝ $\frac{1}{4}$ ，事件B发生的P（B）＝ $\frac{1}{5}$ ，则事件A、B都不发生的概率是．

查看试题解析
15. 如图，为了测量河对岸的塔高AB．可以选与塔底B在同一水平面内的两个基点C与D，现测得CD＝30米，且在点C和D测得塔顶A的仰角分别为45°，30°，又∠CBD＝30°，则塔高AB＝米．

查看试题解析
16. 已知A、B、C是半径为3的球O的球面上的三个点，且∠ACB＝120°，AB＝ $\sqrt{3}$ ， AC＋BC＝2．则三棱锥 $O - A B C$ 的体积为．

查看试题解析

四、解答题

17. 若 $\vec{a}$ ， $\vec{b}$ ， $\vec{c}$ 是同一平面内的三个向量，其中 $\vec{a} =$ （3， $- 1$ ）．

(1)、若 $| \vec{c} | = 2 \sqrt{10}$ ，且 $\vec{a}$ ∥ $\vec{c}$ ，求 $\vec{c}$ 的坐标；

(2)、若 $| \vec{b} | = \frac{\sqrt{10}}{2}$ 且 $\vec{a} + 2 \vec{b}$ 与 $2 \vec{a} - \vec{b}$ 垂直，求 $\vec{a}$ 与 $\vec{b}$ 的夹角 $θ$ ．

查看试题解析
18. 如图，四棱锥P﹣ABCD的底面ABCD为菱形，PB＝PD，E，F分别为AB和PD的中点.

(1)、求证：EF∥平面PBC；

(2)、求证：平面PBD⊥平面PAC．

查看试题解析
19. 我校在2021年的自主招生考试成绩中随机抽取40名学生的笔试成绩，按成绩共分成五组：第1组 $[75$ ， $80)$ ，第2组 $[80$ ， $85)$ ，第3组 $[85$ ， $90)$ ，第4组 $[90$ ， $95)$ ，第5组 $[95$ ， $100]$ ，得到的频率分布直方图如图所示，同时规定成绩在85分以上的学生为“优秀”，成绩小于85分的学生为“良好”，且只有成绩为“优秀”的学生才能获得面试资格．

(1)、根据样本频率分布直方图估计样本的中位数与平均数；

(2)、如果用分层抽样的方法从“优秀”和“良好”的学生中共选出5人，再从这5人中选2人，那么至少有一人是“优秀”的概率是多少？

查看试题解析
20. 已知△ABC的角A，B，C的对边分别为a，b，c，且 $s i n A - s i n C = \frac{b}{a + c} (s i n B - s i n C)$ ．

(1)、求角A；

(2)、从两个条件：① $a = 3$ ；②△ABC的面积为 $3 \sqrt{3}$ 中任选一个作为已知条件，求△ABC周长的取值范围．

查看试题解析
21. 如图，已知四边形ABCD是等腰梯形， $A B = 3 C D$ ，高 $h = \sqrt{3}$ ， $t a n A = \frac{\sqrt{3}}{2}$ ，将它沿对称轴OO₁折叠，使二面角A−OO₁−B为直二面角．

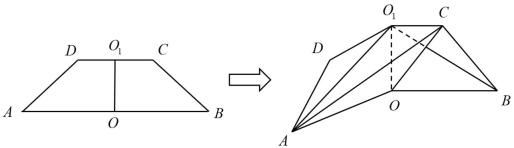(1)、证明：AC⊥BO₁；

(2)、求二面角O−AC−O₁的正弦值．

查看试题解析
22. 已知O为坐标原点，对于函数 $f (x) = a s i n x + b c o s x$ ，称向量 $\vec{O M} = (a ， b)$ 为函数 $f (x)$ 的伴随向量，同时称函数 $f (x)$ 为向量 $\vec{O M}$ 的伴随函数.

(1)、设函数 $g (x) = \sqrt{3} s i n (x - π) - s i n (\frac{3}{2} π - x)$ ，试求 $g (x)$ 的伴随向量 $\vec{O M}$ ；

(2)、记向量 $\vec{O N} = (1 ， \sqrt{3})$ 的伴随函数为 $f (x)$ ，求当 $f (x) = \frac{8}{5}$ 且 $x \in (- \frac{π}{3} ， \frac{π}{6})$ 时 $c o s x$ 的值；

(3)、由（1）中函数 $g (x)$ 的图象（纵坐标不变）横坐标伸长为原来的2倍，再把整个图象向右平移 $\frac{2 π}{3}$ 个单位长度得到 $h (x)$ 的图象，已知 $A (- 2 ， 3)$ ， $B (2 ， 6)$ ，问在 $y = h (x)$ 的图象上是否存在一点P，使得 $\vec{A P} ⊥ \vec{B P}$ .若存在，求出P点坐标；若不存在，说明理由.

查看试题解析