山东省日照市2022年中考数学试卷
试卷更新日期:2022-08-04 类型:中考真卷
一、单选题
-
1. -2的相反数是( )A、-2 B、2 C、 D、2. 山东省第二十五届运动会将于2022年8月25日在日照市开幕,“全民健身与省运同行”成为日照市当前的运动主题.在下列给出的运动图片中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 全民免费接种新冠病毒疫苗是党中央、国务院作出的重大决策部署,通过接种疫苗,让更多人获得免疫力,尽早形成人群免疫屏障,截至2022年5月20日,全国31个省(自治区、直辖市)和新疆生产建设兵团累计报告接种新冠病毒疫苗336905万剂次.数据336905万用科学记数法表示为( )A、0.336905×1010 B、3.36905×1010 C、3.36905×109 D、33.6905×1094. 下列运算正确的是( )A、a6÷a2=a3 B、a4•a2=a6 C、(a2)3=a5 D、a3+a3=a65. 在实数 , x0(x≠0),cos30°,中,有理数的个数是( )A、1个 B、2个 C、3个 D、4个6. 如图,矩形ABCD为一个正在倒水的水杯的截面图,杯中水面与CD的交点为E,当水杯底面BC与水平面的夹角为27°时,∠AED的大小为( )
3. 全民免费接种新冠病毒疫苗是党中央、国务院作出的重大决策部署,通过接种疫苗,让更多人获得免疫力,尽早形成人群免疫屏障,截至2022年5月20日,全国31个省(自治区、直辖市)和新疆生产建设兵团累计报告接种新冠病毒疫苗336905万剂次.数据336905万用科学记数法表示为( )A、0.336905×1010 B、3.36905×1010 C、3.36905×109 D、33.6905×1094. 下列运算正确的是( )A、a6÷a2=a3 B、a4•a2=a6 C、(a2)3=a5 D、a3+a3=a65. 在实数 , x0(x≠0),cos30°,中,有理数的个数是( )A、1个 B、2个 C、3个 D、4个6. 如图,矩形ABCD为一个正在倒水的水杯的截面图,杯中水面与CD的交点为E,当水杯底面BC与水平面的夹角为27°时,∠AED的大小为( ) A、27° B、53° C、57° D、63°7. 下列说法正确的是( )A、一元一次方程的解是x=2 B、在连续5次数学测试中,两名同学的平均成绩相同,则方差较大的同学的成绩更稳定 C、从5名男生,2名女生中抽取3人参加活动,至少会有1名男生被抽中 D、将一次函数y=-2x+5的图象向上平移两个单位,则平移后的函数解析式为y=-2x+18. 《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根木头的长,绳子还剩余4.5尺;将绳子对折再量木头,则木头还剩余1尺,问木头长多少尺?可设木头长为x尺,绳子长为y尺,则所列方程组正确的是( )A、 B、 C、 D、9. 如图,矩形OABC与反比例函数(k1是非零常数,x>0)的图象交于点M,N,与反比例函数(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1-k2=( )
A、27° B、53° C、57° D、63°7. 下列说法正确的是( )A、一元一次方程的解是x=2 B、在连续5次数学测试中,两名同学的平均成绩相同,则方差较大的同学的成绩更稳定 C、从5名男生,2名女生中抽取3人参加活动,至少会有1名男生被抽中 D、将一次函数y=-2x+5的图象向上平移两个单位,则平移后的函数解析式为y=-2x+18. 《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根木头的长,绳子还剩余4.5尺;将绳子对折再量木头,则木头还剩余1尺,问木头长多少尺?可设木头长为x尺,绳子长为y尺,则所列方程组正确的是( )A、 B、 C、 D、9. 如图,矩形OABC与反比例函数(k1是非零常数,x>0)的图象交于点M,N,与反比例函数(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1-k2=( )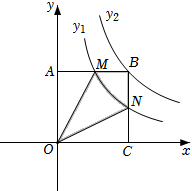 A、3 B、-3 C、 D、10. 如图,几何体是由六个相同的立方体构成的,则该几何体三视图中面积最大的是( )
A、3 B、-3 C、 D、10. 如图,几何体是由六个相同的立方体构成的,则该几何体三视图中面积最大的是( )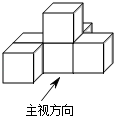 A、主视图 B、左视图 C、俯视图 D、主视图和左视图11. 已知二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为 , 且经过点(-1,0).下列结论:①3a+b=0;②若点 , (3,y2)是抛物线上的两点,则y1<y2;③10b-3c=0;④若y≤c,则0≤x≤3.其中正确的有( )
A、主视图 B、左视图 C、俯视图 D、主视图和左视图11. 已知二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为 , 且经过点(-1,0).下列结论:①3a+b=0;②若点 , (3,y2)是抛物线上的两点,则y1<y2;③10b-3c=0;④若y≤c,则0≤x≤3.其中正确的有( )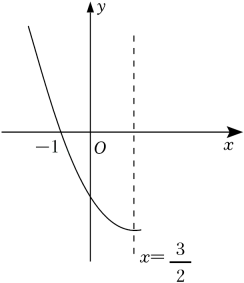 A、1个 B、2个 C、3个 D、4个12. 如图,在平面直角坐标系中,平行四边形OABC的顶点O在坐标原点,点E是对角线AC上一动点(不包含端点),过点E作EFBC,交AB于F,点P在线段EF上.若OA=4,OC=2,∠AOC=45°,EP=3PF,P点的横坐标为m,则m的取值范围是( )
A、1个 B、2个 C、3个 D、4个12. 如图,在平面直角坐标系中,平行四边形OABC的顶点O在坐标原点,点E是对角线AC上一动点(不包含端点),过点E作EFBC,交AB于F,点P在线段EF上.若OA=4,OC=2,∠AOC=45°,EP=3PF,P点的横坐标为m,则m的取值范围是( )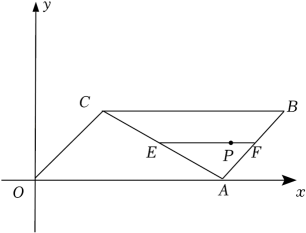 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
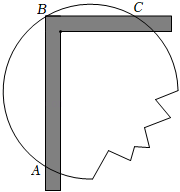
13. 若二次根式在实数范围内有意义,那么x的取值范围是 .14. 一圆形玻璃镜面损坏了一部分,为得到同样大小的镜面,工人师傅用直角尺作如图所示的测量,测得AB=12cm,BC=5cm,则圆形镜面的半径为 .
 15. 关于x的一元二次方程2x2+4mx+m=0有两个不同的实数根x1 , x2 , 且 , 则m= .16. 如图,在平面直角坐标系xOy中,点A的坐标为(0,4),P是x轴上一动点,把线段PA绕点P顺时针旋转60°得到线段PF,连接OF,则线段OF长的最小值是 .
15. 关于x的一元二次方程2x2+4mx+m=0有两个不同的实数根x1 , x2 , 且 , 则m= .16. 如图,在平面直角坐标系xOy中,点A的坐标为(0,4),P是x轴上一动点,把线段PA绕点P顺时针旋转60°得到线段PF,连接OF,则线段OF长的最小值是 .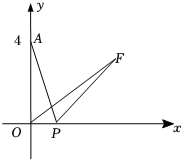
三、解答题
-
17.(1)、先化简再求值: , 其中m=4.(2)、解不等式组并将解集表示在所给的数轴上.
 18. 如图,在Rt△ABC中,∠C=90°,∠B=30°,点D为边AB的中点,点O在边BC上,以点O为圆心的圆过顶点C,与边AB交于点D.
18. 如图,在Rt△ABC中,∠C=90°,∠B=30°,点D为边AB的中点,点O在边BC上,以点O为圆心的圆过顶点C,与边AB交于点D. (1)、求证:直线AB是⊙O的切线;(2)、若 , 求图中阴影部分的面积.19. 今年是中国共产主义青年团成立100周年,某校组织学生观看庆祝大会实况并进行团史学习.现随机抽取部分学生进行团史知识竞赛,并将竞赛成绩(满分100分)进行整理(成绩得分用a表示),其中60≤a<70记为“较差”,70≤a<80记为“一般”,80≤a<90记为“良好”,90≤a≤100记为“优秀”,绘制了不完整的扇形统计图和频数分布直方图.
(1)、求证:直线AB是⊙O的切线;(2)、若 , 求图中阴影部分的面积.19. 今年是中国共产主义青年团成立100周年,某校组织学生观看庆祝大会实况并进行团史学习.现随机抽取部分学生进行团史知识竞赛,并将竞赛成绩(满分100分)进行整理(成绩得分用a表示),其中60≤a<70记为“较差”,70≤a<80记为“一般”,80≤a<90记为“良好”,90≤a≤100记为“优秀”,绘制了不完整的扇形统计图和频数分布直方图.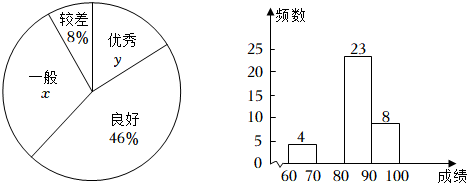
请根据统计图提供的信息,回答如下问题:
(1)、x= ▲ , y= ▲ , 并将直方图补充完整;(2)、已知90≤a≤100这组的具体成绩为93,94,99,91,100,94,96,98,则这8个数据的中位数是 , 众数是;(3)、若该校共有1200人,估计该校学生对团史掌握程度达到优秀的人数;(4)、本次知识竞赛超过95分的学生中有3名女生,1名男生,现从以上4人中随机抽取2人去参加全市的团史知识竞赛,请用列表或画树状图的方法,求恰好抽中2名女生参加知识竞赛的概率.20. 2022年北京冬奥会的成功举办激发了人们对冰雪运动的热情.如图是某滑雪场的横截面示意图,雪道分为AB,BC两部分,小明同学在C点测得雪道BC的坡度i=1:2.4,在A点测得B点的俯角∠DAB=30°.若雪道AB长为270m,雪道BC长为260m.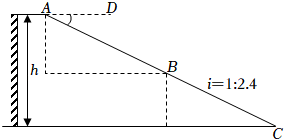 (1)、求该滑雪场的高度h;(2)、据了解,该滑雪场要用两种不同的造雪设备来满足对于雪量和雪质的不同要求,其中甲设备每小时造雪量比乙设备少35m3 , 且甲设备造雪150m3所用的时间与乙设备造雪500m3所用的时间相等.求甲、乙两种设备每小时的造雪量.21. 如图1,△ABC是等腰直角三角形,AC=BC=4,∠C=90°,M,N分别是边AC,BC上的点,以CM,CN为邻边作矩形PMCN,交AB于E,F.设CM=a,CN=b,若ab=8.
(1)、求该滑雪场的高度h;(2)、据了解,该滑雪场要用两种不同的造雪设备来满足对于雪量和雪质的不同要求,其中甲设备每小时造雪量比乙设备少35m3 , 且甲设备造雪150m3所用的时间与乙设备造雪500m3所用的时间相等.求甲、乙两种设备每小时的造雪量.21. 如图1,△ABC是等腰直角三角形,AC=BC=4,∠C=90°,M,N分别是边AC,BC上的点,以CM,CN为邻边作矩形PMCN,交AB于E,F.设CM=a,CN=b,若ab=8.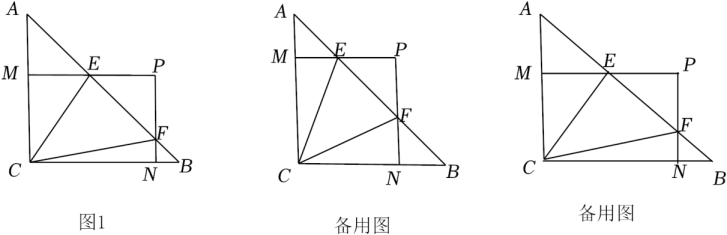 (1)、判断由线段AE,EF,BF组成的三角形的形状,并说明理由;(2)、①当a=b时,求∠ECF的度数;
(1)、判断由线段AE,EF,BF组成的三角形的形状,并说明理由;(2)、①当a=b时,求∠ECF的度数;②当a≠b时,①中的结论是否成立?并说明理由.
22. 在平面直角坐标系xOy中,已知抛物线y=-x2+2mx+3m,点A(3,0).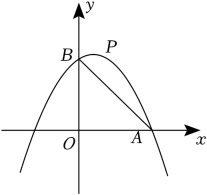 (1)、当抛物线过点A时,求抛物线的解析式;(2)、证明:无论m为何值,抛物线必过定点D,并求出点D的坐标;(3)、在(1)的条件下,抛物线与y轴交于点B,点P是抛物线上位于第一象限的点,连接AB,PD交于点M,PD与y轴交于点N.设S=S△PAM-S△BMN,问是否存在这样的点P,使得S有最大值?若存在,请求出点P的坐标,并求出S的最大值;若不存在,请说明理由.
(1)、当抛物线过点A时,求抛物线的解析式;(2)、证明:无论m为何值,抛物线必过定点D,并求出点D的坐标;(3)、在(1)的条件下,抛物线与y轴交于点B,点P是抛物线上位于第一象限的点,连接AB,PD交于点M,PD与y轴交于点N.设S=S△PAM-S△BMN,问是否存在这样的点P,使得S有最大值?若存在,请求出点P的坐标,并求出S的最大值;若不存在,请说明理由.