山东省济宁市2022年中考数学真题
试卷更新日期:2022-08-04 类型:中考真卷
一、单选题
-
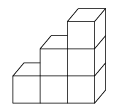
1. 用四舍五入法取近似值,将数0.0158精确到0.001的结果是( )A、0.015 B、0.016 C、0.01 D、0.022. 如图是由6个完全相同的小正方体搭建而成的几何体,则这个几何体的主视图是( )
 A、
A、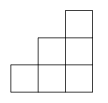 B、
B、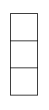 C、
C、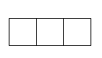 D、
D、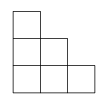 3. 下列各式运算正确的是( )A、 B、 C、 D、4. 下面各式从左到右的变形,属于因式分解的是( )A、 B、 C、 D、5. 某班级开展“共建书香校园”读书活动.统计了1至7月份该班同学每月阅读课外书的本数,并绘制出如图所示的折线统计图.则下列说法正确的是( )
3. 下列各式运算正确的是( )A、 B、 C、 D、4. 下面各式从左到右的变形,属于因式分解的是( )A、 B、 C、 D、5. 某班级开展“共建书香校园”读书活动.统计了1至7月份该班同学每月阅读课外书的本数,并绘制出如图所示的折线统计图.则下列说法正确的是( ) A、从2月到6月,阅读课外书的本数逐月下降 B、从1月到7月,每月阅读课外书本数的最大值比最小值多45 C、每月阅读课外书本数的众数是45 D、每月阅读课外书本数的中位数是586. 一辆汽车开往距出发地420km的目的地,若这辆汽车比原计划每小时多行10km,则提前1小时到达目的地.设这辆汽车原计划的速度是x km/h,根据题意所列方程是( )A、 B、 C、 D、7. 已知圆锥的母线长8cm,底面圆的直径6cm,则这个圆锥的侧面积是( )A、96πcm2 B、48πcm2 C、33πcm2 D、24πcm28. 若关于x的不等式组仅有3个整数解,则a的取值范围是( )A、-4≤a<-2 B、-3<a≤-2 C、-3≤a≤-2 D、-3≤a<-29. 如图,三角形纸片ABC中,∠BAC=90°,AB=2,AC=3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处;再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则AE的长是( )
A、从2月到6月,阅读课外书的本数逐月下降 B、从1月到7月,每月阅读课外书本数的最大值比最小值多45 C、每月阅读课外书本数的众数是45 D、每月阅读课外书本数的中位数是586. 一辆汽车开往距出发地420km的目的地,若这辆汽车比原计划每小时多行10km,则提前1小时到达目的地.设这辆汽车原计划的速度是x km/h,根据题意所列方程是( )A、 B、 C、 D、7. 已知圆锥的母线长8cm,底面圆的直径6cm,则这个圆锥的侧面积是( )A、96πcm2 B、48πcm2 C、33πcm2 D、24πcm28. 若关于x的不等式组仅有3个整数解,则a的取值范围是( )A、-4≤a<-2 B、-3<a≤-2 C、-3≤a≤-2 D、-3≤a<-29. 如图,三角形纸片ABC中,∠BAC=90°,AB=2,AC=3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处;再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则AE的长是( ) A、 B、 C、 D、10. 如图,用相同的圆点按照一定的规律拼出图形.第一幅图4个圆点,第二幅图7个圆点,第三幅图10个圆点,第四幅图13个圆点……按照此规律,第一百幅图中圆点的个数是( )
A、 B、 C、 D、10. 如图,用相同的圆点按照一定的规律拼出图形.第一幅图4个圆点,第二幅图7个圆点,第三幅图10个圆点,第四幅图13个圆点……按照此规律,第一百幅图中圆点的个数是( )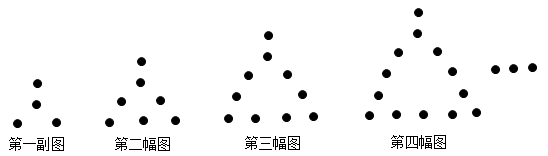 A、297 B、301 C、303 D、400
A、297 B、301 C、303 D、400二、填空题
-
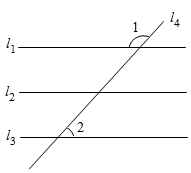
11. 若二次根式 有意义,则x的取值范围是 .12. 如图,直线l1 , l2 , l3被直线l4所截,若l1l2 , l2l3 , ∠1=126°32',则∠2的度数是 .
 13. 已知直线y1=x-1与y2=kx+b相交于点(2,1).请写出b值(写出一个即可),使x>2时,y1>y2 .14. 如图,A是双曲线上的一点,点C是OA的中点,过点C作y轴的垂线,垂足为D,交双曲线于点B,则△ABD的面积是 .
13. 已知直线y1=x-1与y2=kx+b相交于点(2,1).请写出b值(写出一个即可),使x>2时,y1>y2 .14. 如图,A是双曲线上的一点,点C是OA的中点,过点C作y轴的垂线,垂足为D,交双曲线于点B,则△ABD的面积是 .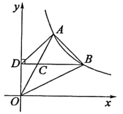
三、解答题
-
15. 已知 , , 求代数式的值.16. 6月5日是世界环境日.某校举行了环保知识竞赛,从全校学生中随机抽取了n名学生的成绩进行分析,并依据分析结果绘制了不完整的统计表和统计图(如下图所示).
学生成绩分布统计表
成绩/分
组中值
频率
75.5≤x<80.5
78
0.05
80.5≤x<85.5
83
a
85.5≤x<90.5
88
0.375
90.5≤x<95.5
93
0.275
95.5≤x<100.5
98
0.05
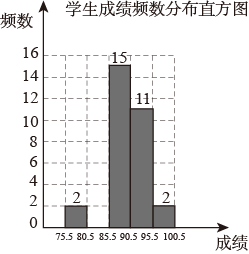
请根据以上图表信息,解答下列问题:
(1)、填空:n= , a=;(2)、请补全频数分布直方图;(3)、求这n名学生成绩的平均分;(4)、从成绩在75.5≤x<80.5和95.5≤x<100.5的学生中任选两名学生.请用列表法或画树状图的方法,求选取的学生成绩在75.5≤x<80.5和95.5≤x<100.5中各一名的概率.17. 如图,在矩形ABCD中,以AB的中点O为圆心,以OA为半径作半圆,连接OD交半圆于点E,在上取点F,使 , 连接BF,DF. (1)、求证:DF与半圆相切;(2)、如果AB=10,BF=6,求矩形ABCD的面积.18. 某运输公司安排甲、乙两种货车24辆恰好一次性将328吨的物资运往A,B两地,两种货车载重量及到A,B两地的运输成本如下表:
(1)、求证:DF与半圆相切;(2)、如果AB=10,BF=6,求矩形ABCD的面积.18. 某运输公司安排甲、乙两种货车24辆恰好一次性将328吨的物资运往A,B两地,两种货车载重量及到A,B两地的运输成本如下表:货车类型
载重量(吨/辆)
运往A地的成本(元/辆)
运往B地的成本(元/辆)
甲种
16
1200
900
乙种
12
1000
750
(1)、求甲、乙两种货车各用了多少辆;(2)、如果前往A地的甲、乙两种货车共12辆,所运物资不少于160吨,其余货车将剩余物资运往B地.设甲、乙两种货车到A,B两地的总运输成本为w元,前往A地的甲种货车为t辆.①写出w与t之间的函数解析式;
②当t为何值时,w最小?最小值是多少?
19. 知识再现:如图1,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.∵ ,
∴ ,
∴
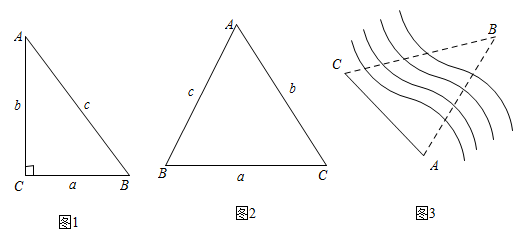 (1)、拓展探究:如图2,在锐角ABC中,∠A,∠B,∠C的对边分别为a,b,c.请探究 , , 之间的关系,并写出探究过程.(2)、解决问题:如图3,为测量点A到河对岸点B的距离,选取与点A在河岸同一侧的点C,测得AC=60m,∠A=75°,∠C=60°.请用拓展探究中的结论,求点A到点B的距离.20. 已知抛物线与x轴有公共点.
(1)、拓展探究:如图2,在锐角ABC中,∠A,∠B,∠C的对边分别为a,b,c.请探究 , , 之间的关系,并写出探究过程.(2)、解决问题:如图3,为测量点A到河对岸点B的距离,选取与点A在河岸同一侧的点C,测得AC=60m,∠A=75°,∠C=60°.请用拓展探究中的结论,求点A到点B的距离.20. 已知抛物线与x轴有公共点.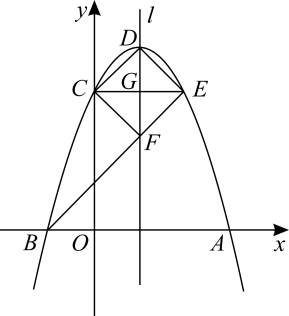 (1)、当y随x的增大而增大时,求自变量x的取值范围;(2)、将抛物线先向上平移4个单位长度,再向右平移n个单位长度得到抛物线(如图所示),抛物线与x轴交于点A,B(点A在点B的右侧),与y轴交于点C.当OC=OA时,求n的值;(3)、D为抛物线的顶点,过点C作抛物线的对称轴l的垂线,垂足为G,交抛物线于点E,连接BE交l于点F.求证:四边形CDEF是正方形.21. 如图,△AOB是等边三角形,过点A作y轴的垂线,垂足为C,点C的坐标为(0,).P是直线AB上在第一象限内的一动点,过点P作y轴的垂线,垂足为D,交AO于点E,连接AD,作DM⊥AD交x轴于点M,交AO于点F,连接BE,BF.
(1)、当y随x的增大而增大时,求自变量x的取值范围;(2)、将抛物线先向上平移4个单位长度,再向右平移n个单位长度得到抛物线(如图所示),抛物线与x轴交于点A,B(点A在点B的右侧),与y轴交于点C.当OC=OA时,求n的值;(3)、D为抛物线的顶点,过点C作抛物线的对称轴l的垂线,垂足为G,交抛物线于点E,连接BE交l于点F.求证:四边形CDEF是正方形.21. 如图,△AOB是等边三角形,过点A作y轴的垂线,垂足为C,点C的坐标为(0,).P是直线AB上在第一象限内的一动点,过点P作y轴的垂线,垂足为D,交AO于点E,连接AD,作DM⊥AD交x轴于点M,交AO于点F,连接BE,BF. (1)、填空:若△AOD是等腰三角形,则点D的坐标为;(2)、当点P在线段AB上运动时(点P不与点A,B重合),设点M的横坐标为m.
(1)、填空:若△AOD是等腰三角形,则点D的坐标为;(2)、当点P在线段AB上运动时(点P不与点A,B重合),设点M的横坐标为m.①求m值最大时点D的坐标;
②是否存在这样的m值,使BE=BF?若存在,求出此时的m值;若不存在,请说明理由.