辽宁省沈阳市2022年中考数学真题
试卷更新日期:2022-08-04 类型:中考真卷
一、单选题
-
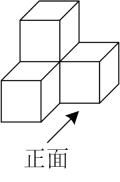
1. 计算正确的是( )A、2 B、-2 C、8 D、-82. 如图是由4个相同的小立方块搭成的几何体,这个几何体的主视图是( )
 A、
A、 B、
B、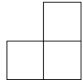 C、
C、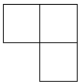 D、
D、 3. 下列计算结果正确的是( )A、 B、 C、 D、4. 在平面直角坐标系中,点关于y轴对称的点的坐标是( )A、 B、 C、 D、5. 调查某少年足球队全体队员的年龄,得到数据结果如下表:
3. 下列计算结果正确的是( )A、 B、 C、 D、4. 在平面直角坐标系中,点关于y轴对称的点的坐标是( )A、 B、 C、 D、5. 调查某少年足球队全体队员的年龄,得到数据结果如下表:年龄/岁
11
12
13
14
15
人数
3
4
7
2
2
则该足球队队员年龄的众数是( )
A、15岁 B、14岁 C、13岁 D、7人6. 不等式的解集在数轴上表示正确的是( )A、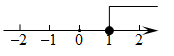 B、
B、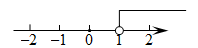 C、
C、 D、
D、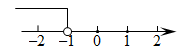 7. 如图,在中, , 点D、E分别是直角边AC、BC的中点,连接DE,则度数是( )
7. 如图,在中, , 点D、E分别是直角边AC、BC的中点,连接DE,则度数是( )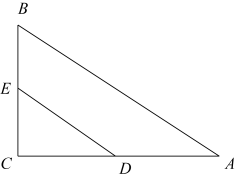 A、70° B、60° C、30° D、20°8. 在平面直角坐标系中,一次函数y=-x+1的图象是( )A、
A、70° B、60° C、30° D、20°8. 在平面直角坐标系中,一次函数y=-x+1的图象是( )A、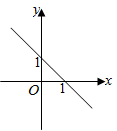 B、
B、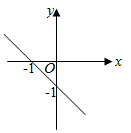 C、
C、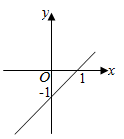 D、
D、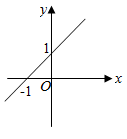 9. 下列说法正确的是( )A、了解一批灯泡的使用寿命,应采用抽样调查的方式 B、如果某彩票的中奖概率是1%,那么一次购买100张这种彩票一定会中奖 C、若甲、乙两组数据的平均数相同, , , 则乙组数据较稳定 D、“任意掷一枚质地均匀的骰子,掷出的点数是7”是必然事件10. 如图,一条河两岸互相平行,为测得此河的宽度PT(PT与河岸PQ垂直),测P、Q两点距离为m米, , 则河宽PT的长度是( )
9. 下列说法正确的是( )A、了解一批灯泡的使用寿命,应采用抽样调查的方式 B、如果某彩票的中奖概率是1%,那么一次购买100张这种彩票一定会中奖 C、若甲、乙两组数据的平均数相同, , , 则乙组数据较稳定 D、“任意掷一枚质地均匀的骰子,掷出的点数是7”是必然事件10. 如图,一条河两岸互相平行,为测得此河的宽度PT(PT与河岸PQ垂直),测P、Q两点距离为m米, , 则河宽PT的长度是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式: .12. 二元一次方程组的解是 .13. 化简: .14. 如图,边长为4的正方形ABCD内接于 , 则的长是(结果保留)
 15. 如图四边形ABCD是平行四边形,CD在x轴上,点B在y轴上,反比例函数的图象经过第一象限点A,且平行四边形ABCD的面积为6,则 .
15. 如图四边形ABCD是平行四边形,CD在x轴上,点B在y轴上,反比例函数的图象经过第一象限点A,且平行四边形ABCD的面积为6,则 .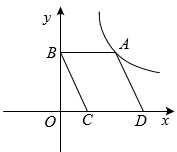 16. 如图,将矩形纸片ABCD折叠,折痕为MN,点M,N分别在边AD,BC上,点C,D的对应点分别在E,F且点F在矩形内部,MF的延长线交BC与点G,EF交边BC于点H. , , 当点H为GN三等分点时,MD的长为 .
16. 如图,将矩形纸片ABCD折叠,折痕为MN,点M,N分别在边AD,BC上,点C,D的对应点分别在E,F且点F在矩形内部,MF的延长线交BC与点G,EF交边BC于点H. , , 当点H为GN三等分点时,MD的长为 .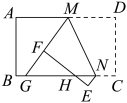
三、解答题
-
17. 计算: .18. 为了调动同学们学习数学的积极性,班内组织开展了“数学小先生”讲题比赛,老师将四道备讲题的题号1,2,3,4,分别写在完全相同的4张卡片的正面,将卡片背面朝上洗匀.(1)、随机抽取一张卡片,卡片上的数字是“4”的概率是;(2)、小明随机抽取两张卡片,用画树状图或列表的方法求两张卡片上的数字是“2”和“3”的概率.19. 如图,在中,AD是的角平分线,分别以点A,D为圆心,大于的长为半径作弧,两弧交于点M,N,作直线MN,分别交AB,AD,AC于点E,O,F,连接DE,DF.
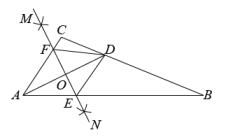 (1)、由作图可知,直线MN是线段AD的 .(2)、求证:四边形AEDF是菱形.20. 某校积极落实“双减”政策,将要开设拓展课程,为让学生可以根据自己的兴趣爱好选择最喜欢的课程,进行问卷调查,问卷设置以下四种选项:A(综合模型)、B(摄影艺术)、C(音乐鉴赏)、D(劳动实践),随机抽取了部分学生进行调查,每名学生必须且只能选择其中最喜欢的一种课程,并将调查结果整理绘制成如下不完整的统计图.
(1)、由作图可知,直线MN是线段AD的 .(2)、求证:四边形AEDF是菱形.20. 某校积极落实“双减”政策,将要开设拓展课程,为让学生可以根据自己的兴趣爱好选择最喜欢的课程,进行问卷调查,问卷设置以下四种选项:A(综合模型)、B(摄影艺术)、C(音乐鉴赏)、D(劳动实践),随机抽取了部分学生进行调查,每名学生必须且只能选择其中最喜欢的一种课程,并将调查结果整理绘制成如下不完整的统计图.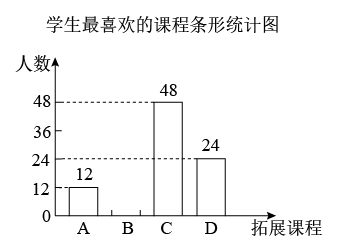

根据以上信息,解答下列问题:
(1)、此次被调查的学生人数为名;(2)、直接在答题卡中补全条形统计图;(3)、求拓展课程D(劳动实践)所对应的扇形的圆心角的度数;(4)、根据抽样调查结果,请你估计该校800名学生中,有多少名学生最喜欢C(音乐鉴赏)拓展课程.21. 如图,用一根长60厘米的铁丝制作一个“日”字型框架ABCD,铁丝恰好全部用完. (1)、若所围成矩形框架ABCD的面积为144平方厘米,则AB的长为多少厘米?(2)、矩形框架ABCD面积最大值为平方厘米.22. 如图,四边形内接于圆 , 是圆的直径, , 的延长线交于点 , 延长交于点 , .
(1)、若所围成矩形框架ABCD的面积为144平方厘米,则AB的长为多少厘米?(2)、矩形框架ABCD面积最大值为平方厘米.22. 如图,四边形内接于圆 , 是圆的直径, , 的延长线交于点 , 延长交于点 , .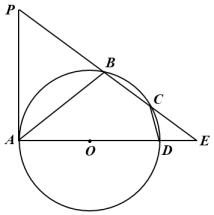 (1)、求证:是圆的切线;(2)、连接 , , , 的长为 .23. 如图,在平面直角坐标系中,一次函数的图象与x轴交于点A,与y轴交于点 , 与直线OC交于点 .
(1)、求证:是圆的切线;(2)、连接 , , , 的长为 .23. 如图,在平面直角坐标系中,一次函数的图象与x轴交于点A,与y轴交于点 , 与直线OC交于点 . (1)、求直线AB的函数表达式;(2)、过点C作轴于点D,将沿射线CB平移得到的三角形记为 , 点A,C,D的对应点分别为 , , , 若与重叠部分的面积为S,平移的距离 , 当点与点B重合时停止运动.
(1)、求直线AB的函数表达式;(2)、过点C作轴于点D,将沿射线CB平移得到的三角形记为 , 点A,C,D的对应点分别为 , , , 若与重叠部分的面积为S,平移的距离 , 当点与点B重合时停止运动.①若直线交直线OC于点E,则线段的长为(用含有m的代数式表示);
②当时,S与m的关系式为;
③当时,m的值为 .
24. 如图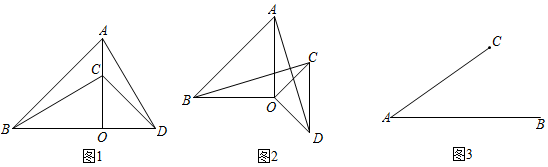 (1)、如图1,和是等腰直角三角形, , 点C在OA上,点D在线段BO延长线上,连接AD,BC.线段AD与BC的数量关系为;(2)、如图2,将图1中的绕点O顺时针旋转()第一问的结论是否仍然成立;如果成立,证明你的结论,若不成立,说明理由.(3)、如图,若 , 点C是线段AB外一动点, , 连接BC,
(1)、如图1,和是等腰直角三角形, , 点C在OA上,点D在线段BO延长线上,连接AD,BC.线段AD与BC的数量关系为;(2)、如图2,将图1中的绕点O顺时针旋转()第一问的结论是否仍然成立;如果成立,证明你的结论,若不成立,说明理由.(3)、如图,若 , 点C是线段AB外一动点, , 连接BC,①若将CB绕点C逆时针旋转90°得到CD,连接AD,则AD的最大值 ▲ ;
②若以BC为斜边作 , (B、C、D三点按顺时针排列), , 连接AD,当时,直接写出AD的值.
25. 如图,平面直角坐标系中,O是坐标原点,抛物线经过点和点与x轴另一个交点A.抛物线与y轴交于点C,作直线AD. (1)、①求抛物线的函数表达式
(1)、①求抛物线的函数表达式②并直接写出直线AD的函数表达式.
(2)、点E是直线AD下方抛物线上一点,连接BE交AD于点F,连接BD,DE,的面积记为 , 的面积记为 , 当时,求点E的坐标;(3)、点G为抛物线的顶点,将抛物线图象中x轴下方部分沿x轴向上翻折,与抛物线剩下部分组成新的曲线为 , 点C的对应点 , 点G的对应点 , 将曲线 , 沿y轴向下平移n个单位长度().曲线与直线BC的公共点中,选两个公共点作点P和点Q,若四边形是平行四边形,直接写出P的坐标.