陕西省渭南市白水县2021-2022学年八年级下学期期末数学试卷

试卷更新日期：2022-08-04 类型：期末考试

进入出卷网下载

一、选择题（共8小题，每小题3分，计24分）

1. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{6}$ B、 $\sqrt{27}$ C、 $\sqrt{\frac{1}{2}}$ D、 $\sqrt{16}$

查看试题解析
2. 下列各组数中，以它们为边长的线段能构成直角三角形的是（）

A、1，2，3 B、1， $\sqrt{2}$ ， $\sqrt{3}$ C、4，5，6 D、12，15，20

查看试题解析
3. 某部队一军人在一次射击训练时，连续10次的成绩为6次10环，1次9环，3次8环，则该军人这10次射击的平均成绩为（）

A、9.2环 B、9.3环 C、9.4环 D、9.5环

查看试题解析
4. 一个正比例函数的图象经过点A（－2，3），B（a，－3），则a的值为（）

A、2 B、－2 C、3 D、－3

查看试题解析
5. 矩形具有而菱形不具有的性质是（）

A、对边相等 B、对角线互相垂直 C、邻边垂直 D、对角线互相平分

查看试题解析
6. 如图，数轴上的点A表示的数是－1，点B表示的数是1， $C B ⊥ A B$ 于点B ，且BC＝2，以点A为圆心，AC为半径在点A右侧画弧交数轴于点D ，则点D表示的数为（）

A、 $2 \sqrt{2}$ B、2.8 C、 $2 \sqrt{2} + 1$ D、 $2 \sqrt{2} - 1$

查看试题解析
7. 直线 $y_{1} = k_{1} x + b$ 与直线 $y_{2} = k_{2} x$ 在同一平面直角坐标系中的图象如图所示，则关于x的不等式 $k_{1} x + b \leq k_{2} x$ 的解集为（）

A、 $x > - 3$ B、 $x < - 3$ C、 $x \leq - 3$ D、 $x \geq - 3$

查看试题解析
8. 如图，在菱形ABCD中，对角线AC与BD相交于点O ， $∠ A B C = 60 °$ ，点E、F分别是BC、CD的中点，BD分别与AE、AF相交于点M、N ，连接OE、OF、EF ，下列结论：① $△ A E F$ 是等边三角形；②四边形CEOF是菱形；③ $O F ⊥ A E$ ；④ $B M = M N = N D$ ，其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（共5小题，每小题3分，计15分）

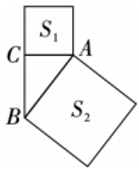
9. 若根式 $\sqrt{2 - x}$ 有意义，则实数x的取值范围是.

查看试题解析
10. 一组数据1，2，5，3，6，6，则这组数据的中位数是．

查看试题解析
11. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，以 $△ A B C$ 的两边AC、AB为边向外作两个正方形， $S_{1}$ 、 $S_{2}$ 分别表示这两个正方形的面积，若 $S_{1} = 8$ ， $S_{2} = 17$ ，则BC＝．

查看试题解析
12. 将直线 $y = k x + 5$ 的图象向下平移3个单位后，经过点A（1，0），则平移后的直线解析式为．

查看试题解析
13. 如图，正方形ABCD和正方形AEFG的边长分别为5 cm和3 cm，点E、G分别为AB、AD边上的点，H为CF的中点，连接HG，则HG的长为cm．

查看试题解析

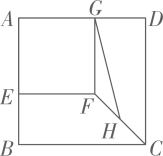
三、解答题（共13小题，计81分，解答应写出过程）

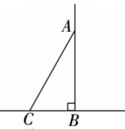
14. 计算： $\sqrt{3} \times \sqrt{6} + \sqrt{24} \div \sqrt{27}$ ．

查看试题解析
15. 如图，将长为6米的梯子AC斜靠在墙上，BC长为2米，求梯子上端A到墙的底端B的距离AB ．

查看试题解析
16. 已知一次函数 $y = (1 - 3 m) x + m - 4$ ，若其函数值y随着x的增大而减小，且其图象不经过第一象限，求m的取值范围．

查看试题解析
17. 已知 $x = \sqrt{5} - 2$ ， $y = \sqrt{5} + 2$ ，求代数式 $x^{2} - y^{2}$ 的值．

查看试题解析
18. 如图，点E是 $▱ A B C D$ 的CD边的中点，AE、BC的延长线交于点F ， $C F = 3$ ， $C E = 2$ ，求 $▱ A B C D$ 的周长．

查看试题解析
19. 如图，一棵高5.4m的大树被台风刮断，测得树梢着地点到树根的距离 $B C = 3.6 m$ ，求大树折断处离地面的高度AB ．

查看试题解析
20. 学校广播站要招收一名播音员，考查形象、知识面、普通话三个项目，按形象占10%，知识面占40%，普通话占50%，计算加权平均数，作为最后评定的总成绩，若总成绩超过85分，则可进入候选名单．已知张强的形象、知识面、普通话三项的成绩依次为90分、80分、90分，计算并说明张强能否进入候选名单？

查看试题解析
21. 如图，在四边形ABCD中， $A B ⊥ A D$ ，AB＝2cm， $A D = \sqrt{5} cm$ ，BC＝4cm，CD＝5cm，求四边形ABCD的面积．

查看试题解析
22. 如图，在 $▱ A B C D$ 中，AE是 $∠ D A B$ 的平分线， $E F ∥ A D$ 交AB、CD于点F、E ，求证：四边形ADEF是菱形．

查看试题解析
23. 如图，一次函数 $y = m x + 2$ 的图象经过点A（2，4）、B（n ，－1），与y轴交于点C ．

(1)、求m ， n的值；

(2)、连接OA ， OB ，求 $△ O A B$ 的面积．

查看试题解析

24. 2022年4月7日是第73个世界卫生日，某学校为纪念爱国卫生运动以及抗击新冠肺炎疫情决定在八年级举办卫生知识竞赛活动．甲，乙两班各选派5名学生参加学校卫生知识竞赛（满分100分）．成绩如下（单位：分）：

甲班：96，92，94，97，96；

乙班；90，98，97，98，92.

通过数据分析，列表如下：

班级	平均分	中位数	众数
甲班	a	96	96
乙班	95	b	c

(1)、填空：a＝， b＝， c＝；

(2)、已知乙班学生竞赛成绩的方差为11.2，请计算甲班学生竞赛成绩的方差，并回答哪个班的学生竞赛成绩更稳定？

查看试题解析

25. 甲、乙两车分别从B ， A两地同时出发，甲车匀速前往A地；乙车匀速前往B地，到达B地立即以另一速度按原路匀速返回到A地；设甲、乙两车距A地的路程为y（千米），乙车行驶的时间为x（时），y与x之间的函数图象如图所示．

(1)、求乙车从B地到达A地过程中的函数关系式，并写出自变量x的取值范围；

(2)、求乙车到达B地时甲车距A地的路程．

查看试题解析
26. 如图1，在 $△ A B C$ 中，点D在BC的延长线上，点O是AC边上的一个动点，过点O作直线 $M N ∥ B C$ ，设MN交 $∠ B C A$ 的平分线于点E，交 $∠ D C A$ 的平分线于点F ．

(1)、线段CE与CF的位置关系是；

(2)、探究：线段OE与OF的数量关系，并加以证明；

(3)、如图2，连接AE ， AF ，当点O运动到何处时，四边形AECF是矩形，并说明理由；

(4)、在（3）的前提下， $△ A B C$ 满足什么条件时，四边形AECF是正方形，请说明理由．

查看试题解析