四川省广元市旺苍县2022年春季义务教育阶段学生学业质量监测八年级下学期数学试卷

试卷更新日期：2022-08-04 类型：期末考试

进入出卷网下载

一、单选题（下列每小题给出的四个选项中，只有一个是符合题意的.每小题3分，共30分）

1. 在下列二次根式中，属于最简二次根式的是（）

A、 $\sqrt{0.1}$ B、 $\sqrt{12}$ C、 $\sqrt{10}$ D、 $\sqrt{27}$

查看试题解析
2. 若 $\sqrt{3 x - 1}$ 有意义，则 $x$ 的取值范围是（）

A、 $x \leq \frac{1}{3}$ B、 $x \geq \frac{1}{3}$ C、 $x > 0$ D、 $x < - 1$

查看试题解析
3. 如果一直角三角形的两边长分别为3和5，则第三边长是（）

A、4 B、 $\sqrt{34}$ C、4或 $\sqrt{34}$ D、以上答案都不正确

查看试题解析
4. 某校举办主题为“关爱身心健康，致敬可爱守护者”的演讲比赛，进入决赛的6名选手的成绩（单位：分）分别为：9.0， 8.4， 9.2， 8.5， 9.2， 9.5，则这组数据的中位数和众数分别是（）

A、9.1， 9.2 B、9.1， 9.5 C、9.0， 9.2 D、8.5， 9.5

查看试题解析
5. 如图，在△ABC中，∠C=90°，AD平分∠BAC交BC于点D，若AD=13，AC=12，则点D到AB的距离为（）

A、3 B、4 C、5 D、6

查看试题解析
6. 对于函数 $y = - 2 x + 1$ ，下列结论正确的是（）

A、它的图象与两坐标轴围成的直角三角形面积为 $\frac{1}{2}$ B、 $y$ 的值随 $x$ 的增大而增大 C、它的图象必经过点（1，-3） D、它的图象不经过第三象限

查看试题解析
7. 菱形ABCD中，对角线AC=5，BD=12.则菱形的高等于（）

A、 $\frac{15}{13}$ B、 $\frac{30}{13}$ C、 $\frac{60}{13}$ D、30

查看试题解析
8. 下列命题中，是假命题的是（）

A、对角线相等的平行四边形是矩形 B、一条对角线平分了一个内角的平行四边形是菱形 C、对角互补的平行四边形是矩形 D、四个角都相等的四边形是菱形

查看试题解析
9. 直线 $y = k x － b$ 经过一、二、三象限，则 $y = b x + k$ 的图象可能是图中的（）

A、 B、 C、 D、

查看试题解析
10. 如图，四边形ABCD是正方形，直线a，b，c分别通过A、D、C三点，且a∥b∥c.若a与b之间的距离是3，b与c之间的距离是5，则正方形ABCD的面积是（）

A、64 B、34 C、30 D、16

查看试题解析

二、填空题（每小题4分，共24分）

11. 如果一组数据4，x，2，3，6的平均数是4，那么x是.

查看试题解析
12. 若代数式 $\frac{\sqrt{m + 1}}{\sqrt{m - 1}}$ 有意义，则 $m$ 的取值范围是.

查看试题解析
13. 如图，一次函数 $y = - 2 x$ 和 $y = k x + b$ 的图象相较于点A（-2，4），则关于 $x$ 的方程 $k x + b + 2 x = 0$ 的解是.

查看试题解析
14. 学校举行演讲比赛，共有15名同学进入决赛，比赛将评出金奖1名，银奖3名，铜奖4名．某参赛选手知道自己的分数后，要判断自己能否获奖，他应当关注的有关成绩的统计量是（填“平均数”、“中位数”或“众数”）．

查看试题解析
15. 如图，在矩形ABCD中，M为BC边上一点，连接AM，过点D作DE⊥AM，垂足为E，若DE＝DC＝1，AE＝2EM，则BM的长为．

查看试题解析
16. 如图，在▱ABCD中，AD=2AB，F是AD的中点，作CE⊥AB于E，在线段AB上，连接EF、CF.则下列结论：①∠BCD=2∠DCF；②∠ECF=∠CEF；③ S_△BEC=2S_△CEF；④∠DFE=3∠AEF；其中一定正确的是.（填写序号）

查看试题解析

三、解答题（要求写出必要的解答步骤或证明过程.共96分）

17. 计算：

(1)、 $\sqrt{27} - \sqrt{12} + \sqrt{\frac{1}{3}}$

(2)、 $（ \sqrt{5} + 1 ） \cdot （ \sqrt{5} - 1 ） + 6 \sqrt{\frac{1}{3}} - （ 1 + \sqrt{3} ）^{2}$

查看试题解析
18. 先化简，在求值： $（ \frac{1 - a}{a + 1} + 1 ） \div \frac{a^{2} - 2 a + 1}{a^{2} -1} ，其中 a = \sqrt{2} + 1$

查看试题解析
19. 某校八年级一班在校园操场一角开辟了一块四边形的小花园，把课堂的“死教材”转换为生动的“活景观”，学生们在课堂上学习理论之余，还可以到小花园实际操练，对生物的发展规律有了更为直观的认识.如图，四边形ABCD是规划好的小花园，经过测量得知： AB=8m，BC=6m，AD=26m，CD=24m，∠ABC=90°，求四边形ABCD的面积.

查看试题解析
20. 如图，CD是△ABC的中线，E为CD上一点，连接AE并延长至点F，使 $E F = A E$ ，连接BF，CF，若CF∥AB．求证：四边形DBFC是平行四边形．

查看试题解析
21. 已知直线y＝k x+b（k≠0）经过点A（3，0），B（1，2）

(1)、求直线y＝k x+b的函数表达式；

(2)、若直线y＝x﹣2与直线y＝k x+b相交于点C，求点C的坐标；

(3)、写出不等式k x+b＞x﹣2的解集．

查看试题解析
22. “珍重生命，注意安全！”同学们在上下学途中一定要注意骑车安全．小明骑单车上学，当他骑了一段时，想起要买某本书，于是又折回到刚经过的新华书店，买到书后继续去学校，以下是他本次所用的时间与路程的关系示意图．根据图中提供信息回答下列问题：

(1)、小明家到学校的路程是多少米？

(2)、小明在书店停留了多少分钟？

(3)、本次上学途中，小明一共行驶了多少米？一共用了多少分钟？

(4)、我们认为骑单车的速度超过300米/分钟就超越了安全限度．问：在整个上学的途中哪个时间段小明骑车速度最快，速度在安全限度内吗？

查看试题解析
23. 受新冠疫情的影响，实体经济受到严重的冲击，“某平台直播带货”迅速成为热潮．某手机专卖店计划购进甲、乙两种手机膜共100件且两种商品都有，并在某平台进行销售，其中，进价、售价如下表：

甲手机膜

乙手机膜

进价（元/件）

5

35

售价（元/件）

10

45

设该专卖店购进甲手机膜x 件（x为正整数），甲、乙手机膜全部销售完后共获得利润y元．

(1)、求y与x的函数关系式，并写出自变量的取值范围；

(2)、若购进的总成本不超过2250元，且购进的手机膜全部售出，怎样进货可使所获利润最大?并求出最大利润．

查看试题解析

24. 甲、乙两名队员参加射击训练，成绩分别被制成下列两个统计图：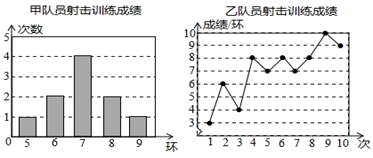

根据以上信息，整理分析数据如下：

	平均成绩/环	中位数/环	众数/环	方差
甲	$a$	$7$	$7$	$1.2$
乙	$7$	$b$	$c$	$d$

(1)、写出表格中

a ， b ， c ， d

的值：

(2)、分别运用表中的四个统计量，简要分析这两名队员的射击训练成绩．若选派其中一名

参赛，你认为应选哪名队员？说明你的理由。

查看试题解析

25. 如图，点E是平行四边形ABCD对角线AC上一点，点F在BE延长线上，且 $E F = B E$ ，EF与CD交于点G．

(1)、求证： $D F / / A C$ ；

(2)、连接DE、CF，若 $2 A B = B F$ ，G恰好是CD的中点，求证：四边形CFDE是矩形．

查看试题解析
26. 已知函数 $y = - \frac{1}{2} x + b$ 的图象与x轴、y轴分别交于点A，B，与函数 $y = 2 x$ 的图象交于点M（2，4）；在x轴上有一动点P，过点P作x轴的垂线，分别交函数 $y = - \frac{1}{2} x + b$ 和 $y = 2 x$ 的图象于点C，D.

(1)、求直线AB的函数关系式及点A的坐标；

(2)、设点p（a，0），若CD＝ $\frac{1}{2}$ OB，求a的值及点C的坐标；

(3)、在 $y$ 轴上是否存在点E，使△OEM为等腰三角形？如果存在，求出点E的坐标；如果不存在，说明理由．

查看试题解析

	甲手机膜	乙手机膜
进价（元/件）	5	35
售价（元/件）	10	45