四川省宜宾市叙州区2021-2022学年七年级下学期期末学业监测数学试卷

试卷更新日期：2022-08-04 类型：期末考试

进入出卷网下载

一、选择题（本大题共12个小题，每小题4分，共48分）

1. 下列方程的解是x＝﹣1的是（）

A、 $\frac{1}{2}$ x+2＝0 B、2x+2＝0 C、3x﹣2＝x D、 $5 x = - \frac{1}{5}$

查看试题解析
2. 下面的图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是（）

A、赵爽弦图 B、科克曲线 C、笛卡尔心形线 D、斐波那契螺旋线

查看试题解析
3. 如果a＞b，那么下列各式一定正确的是（）

A、a²＞b² B、 $\frac{a}{2}$ C、a﹣1＜b﹣1 D、﹣2a＜﹣2b

查看试题解析
4. 若长度分别是a、5、9的三条线段能组成一个三角形，则a的值可以是（）

A、15 B、14 C、8 D、4

查看试题解析
5. 如图，△ABC≌△A'B'C'，其中∠A＝36°，∠C'＝24°，则∠B＝（）

A、60° B、100° C、120° D、135°

查看试题解析
6. 一个正多边形每个内角都等于150°，若用这种多边形拼接地板，需与下列选项中哪正多边形组合（）

A、正四边形 B、正六边形 C、正八边形 D、正三角形

查看试题解析
7. 在等式y＝kx+b中，当x＝﹣1时，y＝﹣2，当x＝2时，y＝7，则这个等式是（）

A、y＝﹣3x+1 B、y＝3x+1 C、y＝2x+3 D、y＝3x﹣1

查看试题解析
8. 《九章算术》中记载“今有共买羊，人出五，不足四十五；人出七，不足三，问人数、羊价各几何？”其大意是：今有人合伙买羊，若每人出5钱，还差45钱；若每人出7钱，还差3钱，问合伙人数、羊价各是多少？此问题中羊价为（）

A、160钱 B、155钱 C、150钱 D、145钱

查看试题解析
9. 如图所示，△ABC的面积是2，AD是△ABC的中线，AF＝ $\frac{1}{3}$ AD，CE＝ $\frac{1}{2}$ EF，则△CDE的面积为（）

A、 $\frac{2}{9}$ B、 $\frac{1}{6}$ C、 $\frac{2}{3}$ D、 $\frac{4}{9}$

查看试题解析
10. 解方程 $\frac{2 x - 1}{3} = \frac{x + a}{2} - 1$ 时，小刚在去分母的过程中，右边的“﹣1”漏乘了公分母6，因而求得方程的解为x＝2，则方程正确的解是（）

A、x＝﹣3 B、x＝﹣2 C、 $x = \frac{1}{3}$ D、 $x = - \frac{1}{3}$

查看试题解析
11. 若关于x的不等式组 ${\begin{array}{l} x - m < 0 \\ 7 - 2 x \leq 1 \end{array}$ 的整数解共有4个，则m的取值范围是（）

A、6＜m＜7 B、6≤m＜7 C、6≤m≤7 D、6＜m≤7

查看试题解析
12. 如图，BP平分∠ABC交CD于点F，DP平分∠ADC交AB于点E，若∠A＝45°，∠P＝40°，则∠C的度数为（）

A、30° B、35° C、40° D、45°

查看试题解析

二、填空题（本大题共6个小题，每小题4分，共24分）.

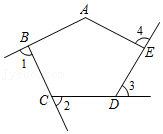
13. 若3x^3k^﹣⁵＝﹣2是关于x的一元一次方程，则k＝．

查看试题解析
14. 不等式 $\frac{x - 1}{3} < 1$ 的非负整数解是．

查看试题解析
15. 如果（x+y﹣5）²+|x﹣y﹣1|＝0，那么 $- 3 x + \frac{1}{2} y$ ＝．

查看试题解析
16. 如图，五边形ABCDE中，∠A＝125°，则∠1+∠2+∠3+∠4的度数是．

查看试题解析
17. 如图，将四边形纸片ABCD沿EF折叠，点A落在A₁处，若∠1+∠2＝88°，则∠A的度数是．

查看试题解析
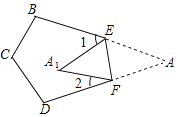18. 如图，在直角三角形ABC中，AC＝3，BC＝4，AB＝5，且AC在直线l上，将△ABC绕点A顺时针旋转到位置①得到点P₁ ，将位置①的三角形绕点P₁顺时针旋转到位置②得到点P₂ ， …，按此规律继续旋转，直到得到点P₂₀₂₃为止（P₁ ， P₂ ， P₃…在直线l上）．则：AP₂₀₂₃＝．

查看试题解析

三、解答题：（本大题共7个小题，共78分）

19. 解下列方程（组）：

(1)、解方程 $\frac{x - 3}{2} - \frac{2 x}{3} = 1$ ；

(2)、解方程组 ${\begin{cases} 3 x - 4 y = 6 ① \\ x + 2 y = 0 ② \end{cases}$ ．

查看试题解析
20. 解答下列问题：

(1)、解不等式 $\frac{x + 1}{3} - 1 \leq \frac{x - 1}{2}$ ，并把解集在数轴上表示出来；

(2)、解不等式组 ${\begin{cases} 4 (x + 1) \leq 7 x + 10 \\ 3 x - 15 < 8 - x \end{cases}$ 并写出所有整数解．

查看试题解析
21. 如图，已知四边形ABCD．

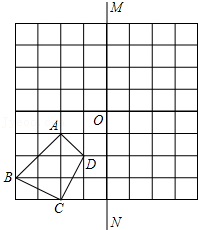
⑴画出四边形ABCD向上平移5格后的四边形A₁B₁C₁D₁；

⑵画出四边形ABCD关于点O成中心对称的四边形A₂B₂C₂D₂；

⑶画出四边形ABCD关于直线MN成轴对称的四边形A₃B₃C₃D₃；

⑷四边形A₂B₂C₂D₂与四边形A₃B₃C₃D₃是否对称？若对称，在图中画出对称轴或对称中心．

查看试题解析
22. 如图，四边形ABCD中，∠A＝∠C＝90°，BE平分∠ABC，DF平分∠ADC，BE、CD交于G点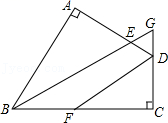

(1)、求证：∠ABC+∠ADC＝180°；

(2)、求证：∠G＝∠CDF．

查看试题解析
23. 已知关于x、y的方程组 ${\begin{cases} x + y = - m - 7 \\ x - y = 3 m + 1 \end{cases}$ 的解满足x≤0，y＜0．

(1)、用含m的代数式分别表示x和y；

(2)、求m的取值范围；

(3)、在m的取值范围内，当m为何整数时，不等式2mx+x＜2m+1的解集为x＞1？

查看试题解析
24. 我市在创建全国文明城市过程中，决定购买A，B两种树苗对某路段道路进行绿化改造，已知购买A种树苗8棵，B种树苗3棵，要950元；若购买A种树苗5棵，B种树苗6棵，则需要800元．

(1)、求购买A，B两种树苗每棵各需多少元？

(2)、考虑到绿化效果和资金周转，购进A种树苗不能少于52棵，且用于购买这两种树苗的资金不能超过7650元，若购进这两种树苗共100棵则有哪几种购买方案？

查看试题解析
25. 如图1，直线m与直线n垂直相交于O，点A在直线m上运动，点B在直线n上运动，AC、BC分别是∠BAO和∠ABO的角平分线．

(1)、∠ACB＝；

(2)、如图2，若BD是△AOB的外角∠OBE的角平分线，BD与AC相交于点D，点A、B在运动的过程中，∠ADB的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值；

(3)、如图3，过C作直线与AB交于F，且满足∠AGO﹣∠BCF＝45°，求证：CF∥OB．

查看试题解析