四川省乐山市2021-2022学年八年级下学期期末数学试卷
试卷更新日期:2022-08-04 类型:期末考试
一、选择题:本大题共12小题,每小题3分,共36分。
-
1. 分式有意义时,x的取值为( )A、 B、 C、 D、且2. 若一组数据2,3,5,x,8的平均数是5,则x的值为( )A、4 B、5 C、6 D、73. 一个矩形的周长为l,若矩形的长为a,则该矩形的宽为( )A、 B、 C、 D、4. 如图,矩形的两对角线相交于点 , 若 , , 则的度数为( )
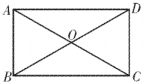 A、 B、 C、 D、5. 若点在第二象限,则的取值范围为( )A、 B、 C、 D、或6. 王老师为了了解学生周末学习时间的情况,在所任班级中随机调查了10名学生,将获得的数据绘制成如图所示的条形图,则这10名学生周末学习的平均时间为( )
A、 B、 C、 D、5. 若点在第二象限,则的取值范围为( )A、 B、 C、 D、或6. 王老师为了了解学生周末学习时间的情况,在所任班级中随机调查了10名学生,将获得的数据绘制成如图所示的条形图,则这10名学生周末学习的平均时间为( )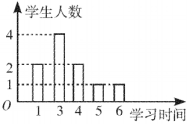 A、1.7 B、3 C、3.3 D、3.77. 如图,在中,的平分线交边于点 . 若 , , 则的长为( )
A、1.7 B、3 C、3.3 D、3.77. 如图,在中,的平分线交边于点 . 若 , , 则的长为( )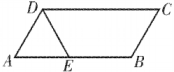 A、 B、2 C、 D、38. 已知直线 , 若 , , 则该直线不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,在菱形中,点在轴上,点的坐标为 , 点的坐标为 , 则点的坐标为( )
A、 B、2 C、 D、38. 已知直线 , 若 , , 则该直线不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,在菱形中,点在轴上,点的坐标为 , 点的坐标为 , 则点的坐标为( )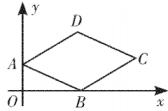 A、 B、 C、 D、10. 已知点和都在直线的图象上,则 , 的大小关系是( )A、 B、 C、 D、 , 的大小不能确定11. 如图,菱形的边长为2, , 点为边的中点,点是对角线上的一动点,则的最小值为( )
A、 B、 C、 D、10. 已知点和都在直线的图象上,则 , 的大小关系是( )A、 B、 C、 D、 , 的大小不能确定11. 如图,菱形的边长为2, , 点为边的中点,点是对角线上的一动点,则的最小值为( )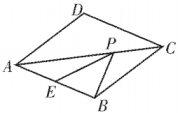 A、 B、 C、2 D、312. 如图,一次函数与反比例函数的图象相交于、两点,与轴,轴分别相交于、两点,连接、 . 过点作轴于点 , 交于点 . 设点的横坐标为 . 若 , 则的值为( )
A、 B、 C、2 D、312. 如图,一次函数与反比例函数的图象相交于、两点,与轴,轴分别相交于、两点,连接、 . 过点作轴于点 , 交于点 . 设点的横坐标为 . 若 , 则的值为( ) A、1 B、 C、2 D、4
A、1 B、 C、2 D、4二、填空题:本大题共6小题,每小题3分,共18分。
-
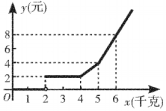
13. 计算14. 一组数据1,3,4,6,7,8的中位数是 .15. 在中,对角线和相交于点 , 若 , 则该一定是(填:矩形或正方形或菱形).16. 如图是某旅行车旅客携带行李收费示意图,小李所携带的行李重20千克,那么小李应该交费(元).
 17. 如图,正方形的边长 , 点为边上一点(不与、重合),以为边在正方形内部做正方形 , 交边于点 , 连结、 , 当是以为顶点的等腰三角形时,的长为 .
17. 如图,正方形的边长 , 点为边上一点(不与、重合),以为边在正方形内部做正方形 , 交边于点 , 连结、 , 当是以为顶点的等腰三角形时,的长为 . 18. 如图,一次函数的图象与轴、轴分别交于、两点,若点在的内部,则的取值范围为 .
18. 如图,一次函数的图象与轴、轴分别交于、两点,若点在的内部,则的取值范围为 .
三、本大题包含第19题、20题、21题,共3小题,每小题8分,共24分。
-
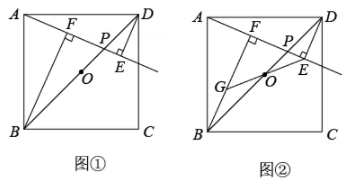
19. 计算: .20. 解方程: .21. 如图,在正方形中,已知、相交于点 , 若 .

求证: .
四、本大题包含第22题、23题、24题,共3小题,每小题9分,共27分。
-
22. 化简 .23. 如图,在中,点为边的中点,连结并延长交的延长线于点 , 连结 .
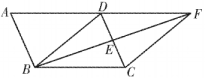
求证:四边形为平行四边形.
24. 某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用(元)与印刷份数(份)之间的关系如图所示: (1)、填空:
(1)、填空:甲种收费的函数关系式是;
乙种收费的函数关系式是;
(2)、该校某年级每次需印制400~450(含100和450)份学案,选择哪种印刷方式较合算?五、本大题包含第25题、26题,共2小题,每小题10分,共20分。
-
25. 某校在八年级举行了一次数学文化知识竞赛,满分10分,学生得分均为整数,成绩超过5分为合格,超过8分为优秀.甲、乙两组学生(各10人)的成绩分布的折线统计图如图所示,成绩统计分布表如下表所示.
 (1)、求出下列成绩统计表中、的值;
(1)、求出下列成绩统计表中、的值;组别
平均分
中位数
方差
合格率
优秀率
甲组
8
7.00
60%
40%
乙组
7.3
2.01
90%
30%
(2)、小李同学说:“这次竞赛我得了8分,在我们小组属于中游偏上!”通过观察,小李应该是哪一组的?(3)、乙组同学说他们组的合格率远高于甲组,所以他们组的成绩好于甲组,但甲组的同学不同意乙组同学的说法,认为他们组的成绩好于乙组.请你给出两条支持乙组同学观点的理由.26. 如图,点、分别在反比例函数和的图象上,线段与轴相交于点 .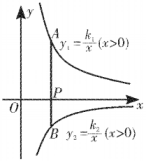
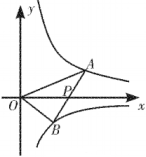
图① 图②
(1)、如图①,若轴,且 , . 求、的值;(2)、如图②,若点是线段的中点,且的面积为2.求的值.六、本大题共2小题,第27题12分,第28题13分,共25分。