广西钦州市浦北县2021-2022学年七年级下学期期末数学试卷

试卷更新日期：2022-08-04 类型：期末考试

进入出卷网下载

一、选择题（本大题共12小题，每小题3分，共36分，在每小题给出的四个选项中只有一项是符合要求的，请用2B铅笔把答题卡上对应题目的答案标号涂黑.）

1. 下列各数中，是无理数的是（）

A、 $- \frac{1}{3}$ B、0 C、 $\sqrt[3]{3}$ D、 $\sqrt{4}$

查看试题解析
2. 以下调查中，适宜采用抽样调查的是（）

A、调查某批次汽车的抗撞击能力 B、了解七（2）班学生的视力情况 C、学校招聘，对应聘人员进行面试 D、汽车站对乘客的行程卡”及“健康码”查验

查看试题解析
3. 如图，量得直线l外一点P到l的距离PB的长为6cm，若点A是直线l上的一点，那么线段PA的长不可能是（）

A、5.5cm B、6.2cm C、7.5cm D、8cm

查看试题解析
4. 下列各组数中，是二元一次方程2x﹣y＝﹣6的解的是（）

A、 ${\begin{array}{l} x = - 2 \\ y = - 2 \end{array}$ B、 ${\begin{array}{l} x = 0 \\ y = - 6 \end{array}$ C、 ${\begin{array}{l} x = 1 \\ y = 8 \end{array}$ D、 ${\begin{array}{l} x = 3 \\ y = 1 \end{array}$

查看试题解析
5. 如图，直线AB∥CD ，则下列结论正确的是（）

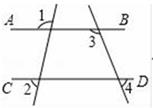A、∠1＝∠2 B、∠3＝∠4 C、∠1+∠3＝180° D、∠3+∠4＝180°

查看试题解析
6. 如果点P（﹣2，n）在第二象限，则n的取值范围是（）

A、n＜0 B、n＞0 C、n≤0 D、n≥0

查看试题解析
7. 空气是由多种气体混合而成的，为了简明扼要地反映各种气体的占比，最适合使用的统计图是（）

A、扇形图 B、条形图 C、折线图 D、直方图

查看试题解析
8. 如图，小玮从A处沿北偏东40°方向行走到点B处，又从点B处沿东偏南23°方向行走到点C处，则∠ABC的度数为（）

A、99° B、107° C、127° D、129°

查看试题解析
9. 已知m＞n，q＜0，则下列不等式一定成立的是（）

A、m+n＞q B、mq＜nq C、 $\frac{m}{q} ＞ \frac{n}{q}$ D、mn＞q

查看试题解析
10. 如图，P，Q两点的坐标分别为（5，a），（b，7），则点（6﹣b，a﹣10）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
11. 《九章算术》是中国古代张苍、秋寿昌所撰写的一部数学专著，其中有一个方程问题：五只雀、六只燕共重16两，燕重雀轻，互换其中一只，恰好一样重．假设每只雀的重量为x两，每只燕的重量为y两，根据题意，则可列出的方程组是（）

A、 ${\begin{array}{l} 6 x + 5 y = 16 \\ 4 x + y = 5 x + y \end{array}$ B、 ${\begin{array}{l} 6 x + 5 y = 16 \\ x + 4 y = 5 x + y \end{array}$ C、 ${\begin{array}{l} 5 x + 6 y = 16 \\ 4 y + x = 5 x + y \end{array}$ D、 ${\begin{array}{l} 5 x + 6 y = 16 \\ 4 x + y = 5 y + x \end{array}$

查看试题解析
12. 对任意两个实数a，b定义两种运算：a⊕b $= {\begin{array}{l} a (a \geq b) \\ b (a ＜ b) \end{array}$ ， a⊗b $= {\begin{array}{l} b (a \geq b) \\ a (a ＜ b) \end{array}$ ，并且定义运算顺序仍然是先做括号内的，例如（﹣2）⊕3＝3，（﹣2）⊗3＝﹣2，[（﹣2）⊕3]⊗2＝2，那么（ $\sqrt{5}$ ⊕2）⊗ $\sqrt[3]{27}$ 的值为（）

A、2 B、 $\sqrt{5}$ C、3 D、3 $\sqrt{5}$

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分.）

13. 一个正方形的面积为7，则它的边长为．

查看试题解析
14. 在平面直角坐标系中，点（﹣3，﹣4）到y轴的距离为．

查看试题解析
15. 小华想了解光明小区500户家庭的教育费用支出情况，随机抽查了该小区的50户家庭并做了相关统计．在这次调查中，样本容量是．

查看试题解析
16. 如图，把一张长方形纸片ABCD沿EF折叠后ED与BC交于点G，D，C分别在M，N的位置上，若∠EFG＝55°，则∠2﹣∠1＝．

查看试题解析
17. 若不等式组 ${\begin{array}{l} x - m ＞ 0 \\ 2 x + 1 ＞ 3 \end{array}$ 的解集为x＞1，则m的取值范围是．

查看试题解析
18. 如图，在长方形ABCD中，放入6个形状、大小相同的小长方形，则图中阴影部分面积为．

查看试题解析

三、解答题（本大题共7小题，共66分.解答应写出文字说明、证明过程或演算步骤.）

19.

(1)、计算： $\sqrt{6}$ （2 $- \sqrt{6}$ ）；

(2)、求x的值：（x+1）²＝4．

查看试题解析
20. 解方程组： ${\begin{array}{l} \end{array} \begin{matrix} x + 2 y = 1 \\ 3 x - 2 y = 11 \end{matrix}$ .

查看试题解析
21. 解不等式组： ${\begin{array}{l} x - 3 (x - 2) \leq 4 \\ \frac{1 + 2 x}{3} ＞ x - 1 \end{array}$ ，并利用数轴确定不等式组的解集．

查看试题解析
22. 在平面直角坐标系中，已知三角形ABC三个顶点坐标分别为A（﹣1，0），B（﹣3，﹣2），C（0，﹣3）．如图，点B在边长为1的正方形网格上．

⑴建立适当的平面直角坐标系，并画出三角形ABC；

⑵将角形ABC向右平移3个单位长度，再向上平移1个单位长度，得到三角形A₁B₁C₁ ，请画出三角形A₁B₁C₁ ，并写出点B₁的坐标；

⑶在（2）的条件下，连接AA₁ ， CC₁ ，并判断它们的位置及大小关系．

查看试题解析

23. 暑假将至，为了增强学生的安全意识，预防溺水事故的发生，启航中学举办了防漏水安全知识竞赛（满分100分），该校2000名学生都参加了知识竞赛．现随机抽取了部分学生的竞赛成绩进行调查研究，收集数据如下：

85 95 88 68 88 86 95 93 87 93 98 99 88 99 97 80 85 92 94 84 80 78 90 98 85 96 98 86 93 80 86 99 82 78 98 88 99 76 88 99

整理、描述及分析数据：

成绩x（单位：分）	频数（人数）
60≤x＜70	1
70≤x＜80	a
80≤x＜90	17
90≤x＜100	c

(1)、直接写出a，c的值：a＝， c＝；

(2)、补充完整频数分布直方图；

(3)、学校决定表彰取得优秀成绩（80分及以上）的学生，请估计该校约有多少人将获得表彰；

(4)、参加学校组织的防溺水安全教育后，请用一句话写出你最深的感悟．

查看试题解析

24. 百货商店抓住旅游文化艺术节商机，决定购进甲、乙两种纪念品若购进甲种纪念品1件，乙种纪念品2件，需要160元：购进甲种纪念品2件，乙种纪念品3件，需要280元．

(1)、购进甲、乙两种纪念品每件各需要多少元？

(2)、该商店决定购进甲、乙两种纪念品共100件，并且考虑市场需求和资金周转，用于购买这些纪念品的资金不少于6300元，同时又不能超过6430元，则该商店共有几种进货方案？

(3)、若销售每件甲种纪念品可获利30元，销售每件乙种纪念品可获利12元，在第（2）问中的各种进货方案中，哪种方案获利最大？最大利润是多少元？

查看试题解析
25. 如图

(1)、【特例发现】
如图1，AB∥CD，CE平分∠ACD，AE平分∠BAC．求∠AEC的度数；

(2)、【类比探究】
如图2，点M是AE上一点，当∠E＝90°保持不变，移动直角顶点E，使CE平分∠MCD．请探究∠BAE与∠MCD的数量关系；

(3)、【拓展应用】
如图3，P为线段AC上一定点，点2为直线CD上一动点，点Q不与点C重合．此时，∠CPQ+∠CQP与∠BAC有什么数量关系？猜想结论并说明理由．

查看试题解析