陕西省渭南市韩城市2021-2022学年八年级下学期期末数学试卷

试卷更新日期：2022-08-04 类型：期末考试

进入出卷网下载

一、单选题

1. 二次根式 $\sqrt{2 - x}$ 有意义，则x的取值范围是（　　）

A、x＞2 B、x＜2 C、x≥2 D、x≤2

查看试题解析
2. 下列各组数中，是勾股数的是（）

A、1， $\sqrt{5}$ ， 3 B、0.3，0.4，0.6 C、9，12，15 D、5，6，7

查看试题解析
3. 某中学规定学生的学期数学成绩满分100分．其中平时成绩占20%，期中考试成绩占30%，期末考试成绩占50%．小彤的三项成绩（百分制）依次为95，90，94，则小彤这学期的数学成绩为（）

A、90分 B、93分 C、95分 D、96分

查看试题解析
4. 若一个正比例函数的图象经过点A（1，﹣4），B（m，8）两点，则m的值为（）

A、2 B、﹣2 C、4 D、﹣4

查看试题解析
5. 平行四边形和矩形都具有的性质是（）

A、每条对角线平分一组对角 B、对角线互相垂直 C、对角线相等 D、对角线互相平分

查看试题解析
6. 如图，图中所有的三角形都是直角三角形、所有的四边形都是正方形，其中A，B，C，D四个小正方形的面积之和等于12，则最大的正方形的边长为（）

A、 $\sqrt{6}$ B、2 $\sqrt{3}$ C、3 D、4

查看试题解析
7. 直线 $l_{1} ： y = k_{1} x + b$ 与直线 $l_{2} ： y = k_{2} x$ 在同一平面直角坐标系中的位置如图所示，则关于 $x$ 的不等式 $k_{1} x + b > k_{2} x$ 的解集为（）

A、 $x > - 1$ B、 $x < - 1$ C、 $x > - 2$ D、 $x < - 2$

查看试题解析
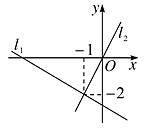8. 如图，在正方形ABCD中，AB=2，E是CD的中点，将△BCE沿BE翻折至△BFE，G是BE的中点，连接FG，则FG的长度是（）

A、 $\sqrt{5}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{\sqrt{5}}{2}$ D、 $\frac{2 \sqrt{5}}{5}$

查看试题解析

二、填空题

9. 计算： $\sqrt{{(\sqrt{5} - 3)}^{2}} =$ ．

查看试题解析
10. 若一组数据5，2，1，7，x，5的中位数为4，则x=.

查看试题解析
11. 已知一次函数 $y = (4 - 2 m) x + 2$ ，函数值 $y$ 随着自变量 $x$ 的值增大而减小，那么常数 $m$ 的取值范围是．

查看试题解析
12. 如图，在数轴上，点A、B表示的数分别为0、2，BC⊥AB于点B，且BC=1，连接AC，在AC上截取CD=BC，以A为圆心，AD的长为半径画弧，交线段AB于点E，则点E表示的实数是.

查看试题解析
13. 如图，在菱形ABCD中， $A B = 13 cm$ ， $A C = 24 cm$ ，E，F分别是CD和BC的中点，连接EF并延长与AB的延长线相交于点G，则EG的长度为cm．

查看试题解析

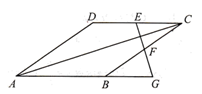
三、解答题

14. 计算： $\sqrt{3} \times \sqrt{15} - \sqrt{20} + \sqrt{\frac{5}{9}}$

查看试题解析
15. 已知y关于x的函数y＝（1﹣3k）x＋2k﹣2，试回答：

(1)、k为何值时，图象过原点？

(2)、当k＝0时，写出该函数图象经过的象限．

查看试题解析
16. 已知在△ABC中，∠C=90°，BC=2 $\sqrt{3}$ +1，AC=2 $\sqrt{3}$ -1，求AB的长．

查看试题解析
17. 若矩形的面积是（6+2 $\sqrt{6}$ ）cm²，一边长是 $\sqrt{6}$ cm，求它的周长．

查看试题解析
18. 如图，E、F分别是矩形ABCD的边AD、BC上的点，且 $A E = C F$ ．求证：四边形 $E B F D$ 为平行四边形．

查看试题解析
19. 如图，在四边形草地ABCD中，AB=1m，BC=2m，CD=2m，AD=3m，且AB⊥BC．求四边形草地ABCD的面积．

查看试题解析
20. 21世纪已经进入了中国太空时代，2021年到2022年，我国通过11次航天发射完成空间站建设，空间站由“天和”楼心舱、“问天”和“梦天”两个实验舱，我国空间站的建成将为开展太空实验及更广泛的国际合作提供精彩舞台．校团委以此为契机，组织了“中国梦·航天情”系列活动．下面是八年级甲、乙两个班各项目的成绩（单位：分）：
项目班次
知识竞赛
演讲比赛
甲
80
90
乙
95
82
如果将知识竞赛、演讲比赛的成绩按4：6的比例确定最终成绩，请通过计算说明甲、乙两个班谁的最终成绩较高．

查看试题解析
21. 如图，车高AC=4m，货车卸货时后面挡板AB弯折落在地面A₁处，已知点A、B、C 在一条直线上，AC⊥A₁C，经过测量A₁C=2m，求BC的长．

查看试题解析
22. 如图，平面直角坐标系中，函数y=kx+2的图象过点A（3，0），将其图象向上平移2 个单位后与x轴交于点B，与y轴交于点C．

(1)、求图象经过点B和点C的一次函数解析式；

(2)、求△OBC的面积

查看试题解析
23. 如图，四边形ABCD的对角线AC、BD交于点O，已知O是AC的中点，AE=CF，DF∥BE．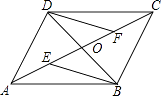

(1)、求证：△BOE≌△DOF；

(2)、若OD= $\frac{1}{2}$ AC，则四边形ABCD是什么特殊四边形？请证明你的结论．

查看试题解析
24. 为了倡导居民节约用水，生活用水按阶梯式水价计费，如图是居民每户每月的水费y（元）与所用的水量x（吨）之间的函数图象，请根据图象所提供的信息，解答下列问题：

(1)、当用水量不超过10吨时，每吨水收费元；

(2)、当用水量超过10吨且不超过30吨时，求y与x之间的函数解析式；

(3)、某户居民四、五月份水费共85元，且五月份用水量小于30吨，五月份用水比四月份多5吨，求这户居民四月份用水多少吨．

查看试题解析

25. 为进一步宣传防震减灾科普知识，增强学生应急避险和自救互救能力，某中学举行“防震减灾知识测试”，初、高中部各选出5名选手组成初中代表队和高中代表队参加学校比赛，根据这10人的比赛成绩（满分为100分），制作统计图及统计表：

	平均数	中位数	众数	方差
初中部	*	85	b	70
高中部	85	a	100	*

(1)、根据以上图表提供的数据填空：a =；b=；

(2)、结合两队成绩的平均数和中位数，分析哪个代表队的比赛成绩较好；

(3)、根据表中的数据，试通过计算说明，哪个代表队的成绩比较稳定?

查看试题解析

26.
如图1，在正方形ABCD中，P是对角线BD上的一点，点E在AD的延长线上，且PA=PE，PE交CD于F．

(1)、证明：PC=PE；

(2)、求∠CPE的度数；

(3)、
如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC=120°时，连接CE，试探究线段AP与线段CE的数量关系，并说明理由．

查看试题解析

项目班次	知识竞赛	演讲比赛
甲	80	90
乙	95	82