陕西省渭南市大荔县2021-2022学年八年级下学期期末数学试卷
试卷更新日期:2022-08-04 类型:期末考试
一、单选题
-
1. 若有意义,则a一定是( )A、正数 B、负数 C、非正数 D、非负数2. 下列曲线中表示y是x的函数的是( )A、
 B、
B、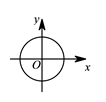 C、
C、 D、
D、 3. 分式方程的解为( )A、 B、 C、 D、4. 如图,在中,DE平分 , , 则( )
3. 分式方程的解为( )A、 B、 C、 D、4. 如图,在中,DE平分 , , 则( )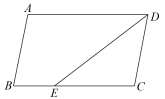 A、30° B、45° C、60° D、80°5. 如图,以 的三边为直角边分别向外作等腰直角三角形.若 ,则图中阴影部分的面积为( )
A、30° B、45° C、60° D、80°5. 如图,以 的三边为直角边分别向外作等腰直角三角形.若 ,则图中阴影部分的面积为( )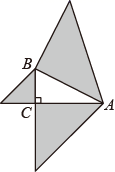 A、3 B、 C、 D、6. 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(0,2),点B的坐标为(﹣3,0),则点C到y轴的距离是( )
A、3 B、 C、 D、6. 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(0,2),点B的坐标为(﹣3,0),则点C到y轴的距离是( )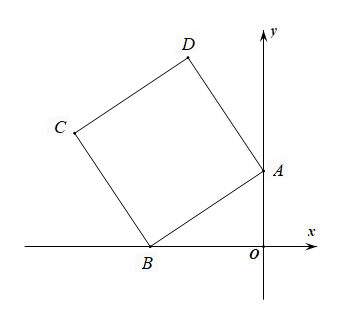 A、6 B、5 C、4 D、37. 为落实“双减”政策,学校随机调查了部分学生一周平均每天的睡眠时间,统计结果如表,则这些被调查学生睡眠时间的众数和中位数分别是( )
A、6 B、5 C、4 D、37. 为落实“双减”政策,学校随机调查了部分学生一周平均每天的睡眠时间,统计结果如表,则这些被调查学生睡眠时间的众数和中位数分别是( )时间/小时
7
8
9
10
人数
6
9
11
4
A、9,8.5 B、9,9 C、10,9 D、11,8.5二、填空题
-
8. 已知实数在数轴上的位置如图所示,则化简的结果为 .
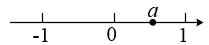 9. 将直线向下平移4个单位,平移后的直线解析式为 .10. 规定 , , 则;11. 如图,点E、F分别是正方形 的边 、 上的点,且 ,已知 ,则图中阴影部分的面积是.
9. 将直线向下平移4个单位,平移后的直线解析式为 .10. 规定 , , 则;11. 如图,点E、F分别是正方形 的边 、 上的点,且 ,已知 ,则图中阴影部分的面积是. 12. 如图,菱形ABCD的对角线AC,BD相交于点O,点P为AB边上一动点(不与点A,B重合),于点E,于点F,若 , , 则EF的最小值为 .
12. 如图,菱形ABCD的对角线AC,BD相交于点O,点P为AB边上一动点(不与点A,B重合),于点E,于点F,若 , , 则EF的最小值为 .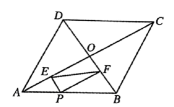
三、解答题
-
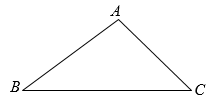
13. 计算: .14. 计算:15. 当时,求的值.16. 如图,已知 , 请用尺规作图法在BC边上找一点P,使得 . (不写作法,保留作图痕迹)
 17. 体育强则国强,国运兴则体育兴.“双减”落地助力体育锻炼的升温,北京冬奥会激发体育锻炼的热情.“双减”携手“冬奥”,将有助于进一步深化体教融合,全面推动青少年体育事业的健康发展.某校体育部甲、乙两名同学为了更好地了解全校学生假期体育锻炼情况,分别随机调查了20名学生平均每天用于体育锻炼的时间,将收集到的数据进行了整理,部分信息如下:
17. 体育强则国强,国运兴则体育兴.“双减”落地助力体育锻炼的升温,北京冬奥会激发体育锻炼的热情.“双减”携手“冬奥”,将有助于进一步深化体教融合,全面推动青少年体育事业的健康发展.某校体育部甲、乙两名同学为了更好地了解全校学生假期体育锻炼情况,分别随机调查了20名学生平均每天用于体育锻炼的时间,将收集到的数据进行了整理,部分信息如下:数据收集:甲同学从全校随机抽取20名学生,平均每天用于体育锻炼的时间如下(单位:分钟):
10,15,20,40,42,43,60,65,70,71,71,71,80,85,85,90,107,120,125,130.
乙同学从九年级随机抽取20名学生,平均每天用于体育锻炼的时间如下(单位:分钟):
10,18,25,30,40,42,55,60,70,76,82,82,86,90,98,100,102,114,120,140.
数据描述:将体育锻炼时间分为四个等级: , , , .
甲同学按如表整理样本数据:
等级
A
B
C
D
人数
3
9
3
分析数据:样本数据的平均数、中位数、众数如表所示:
平均数
中位数
众数
甲
70
71
乙
72
79
乙同学绘制扇形统计图如图:

根据以上信息,回答下列问题:
(1)、填空: , , , ;(2)、若该校学生有1500人,请估计平均每天用于体育锻炼的时间在80分钟(含80分钟)以上的学生有多少人?18. 如图, , 点C在OA边上,OA=36cm,OB=12cm,点P从点A出发,沿着AO方向匀速运动,点Q同时从点B出发,以相同的速度沿BC方向匀速运动,P、Q两点恰好在C点相遇,求BC的长度? 19. 如图, , , , 过C作 , 连接AF与BC相交于点G,若 , 求的度数.
19. 如图, , , , 过C作 , 连接AF与BC相交于点G,若 , 求的度数.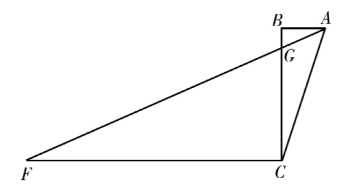 20. 如图,△ABC中,D,E分别为AB,BC的中点,DG⊥AC,EF⊥AC,垂足分别为G,F.
20. 如图,△ABC中,D,E分别为AB,BC的中点,DG⊥AC,EF⊥AC,垂足分别为G,F.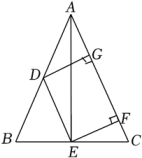 (1)、求证:四边形DEFG为矩形;(2)、若AB=AC=2 , EF=2,求CF的长.21. 某健身俱乐部每次健身费用为25元.暑期来临之际,该俱乐部面向学生推出了两种暑期优惠方案,方案一:购买一张50元的学生暑期专享卡,每次健身费用按六折优惠;方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.设某学生暑期健身x次,按照方案一所需费用为y1(元),按照方案二所需费用为y2(元).(1)、分别写出y1和y2与x的关系式;(2)、小明同学计划暑期前往该俱乐部健身9次,通过计算说明选择哪种方案费用少?22. 如图,在中, , 延长BA到点D,使 , 点E、F分别为边BC、AC的中点.
(1)、求证:四边形DEFG为矩形;(2)、若AB=AC=2 , EF=2,求CF的长.21. 某健身俱乐部每次健身费用为25元.暑期来临之际,该俱乐部面向学生推出了两种暑期优惠方案,方案一:购买一张50元的学生暑期专享卡,每次健身费用按六折优惠;方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.设某学生暑期健身x次,按照方案一所需费用为y1(元),按照方案二所需费用为y2(元).(1)、分别写出y1和y2与x的关系式;(2)、小明同学计划暑期前往该俱乐部健身9次,通过计算说明选择哪种方案费用少?22. 如图,在中, , 延长BA到点D,使 , 点E、F分别为边BC、AC的中点.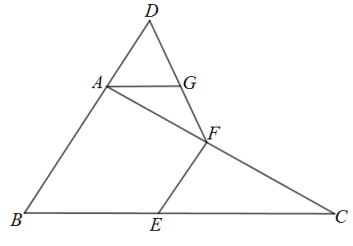 (1)、求证:;(2)、过点A作 , 交DF于点G,求证: .23. 如图,一次函数的图象与轴相交于点 , 与过点的一次函数的图象相交于点 .
(1)、求证:;(2)、过点A作 , 交DF于点G,求证: .23. 如图,一次函数的图象与轴相交于点 , 与过点的一次函数的图象相交于点 .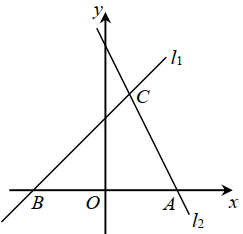 (1)、求一次函数图象相应的函数表达式;(2)、求的面积.24. 问题提出
(1)、求一次函数图象相应的函数表达式;(2)、求的面积.24. 问题提出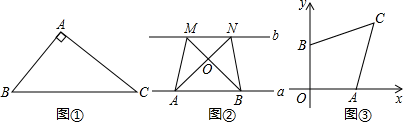 (1)、如图①,在Rt△ABC中,∠A=90°,AB=3,AC=4,在BC上找一点D,使得AD将△ABC分成面积相等的两部分,作出线段AD,并求出AD的长度;
(1)、如图①,在Rt△ABC中,∠A=90°,AB=3,AC=4,在BC上找一点D,使得AD将△ABC分成面积相等的两部分,作出线段AD,并求出AD的长度;问题探究
(2)、如图②,点A、B在直线a上,点M、N在直线b上,且a∥b,连接AN、BM交于点O,连接AM、BN,试判断△AOM与△BON的面积关系,并说明你的理由;解决问题
(3)、如图③,刘老伯有一个形状为筝形OACB的养鸡场,在平面直角坐标系中,O(0,0)、A(4,0)、B(0,4)、C(6,6),是否在边AC上存在一点P,使得过B、P两点修一道笔直的墙(墙的宽度不计),将这个养鸡场分成面积相等的两部分?若存在,请求出直线BP的表达式;若不存在,请说明理由.