湖南省长沙市雨花区2021-2022学年八年级下学期期末数学试卷

试卷更新日期：2022-08-04 类型：期末考试

进入出卷网下载

一、单选题

1. 方程 $x^{2} = x$ 的解是（）

A、 $x = 1$ B、 $x = 0$ C、 $x_{1} = 1$ ， $x_{2} = 0$ D、 $x_{1} = - 1$ ， $x_{2} = 0$

查看试题解析
2. 下列说法正确的是（）

A、有一个角是直角的平行四边形是正方形 B、对角线互相垂直的矩形是正方形 C、有一组邻边相等的菱形是正方形 D、各边都相等的四边形是正方形

查看试题解析
3. 若 $\sqrt{5} = a$ ，则 $\sqrt{80}$ 等于（）

A、 $8 a$ B、 $16 a$ C、 $4 a$ D、 $2 a$

查看试题解析
4. 如图，在▱ABCD中，连接AC，若∠ABC=∠CAD=60°，AB=3，则AD的长是（）．

A、3 B、6 C、8 D、9

查看试题解析
5. 若 $α$ 、 $β$ 是一元二次方程 $x^{2} + 2 x - 2022 = 0$ 的两个实数根，则 $α β$ 的值为（）．

A、2 B、-2 C、2022 D、-2022

查看试题解析
6. 在同一直角坐标系中，一次函数y＝kx＋k与正比例函数y＝kx的图像可能是（）

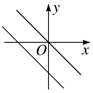A、 B、 C、 D、

查看试题解析
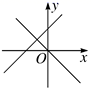7. “赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为a，较短直角边长为b，若（a+b）²=21，大正方形的面积为13，则小正方形的面积为（）

A、3 B、4 C、5 D、6

查看试题解析
8. 如图是根据某班40名同学一周的体育锻炼情况绘制的统计图，该班40名同学一周参加体育锻炼时间的中位数，众数分别是（）

A、10.5，16 B、8.5，16 C、8.5，8 D、9，8

查看试题解析
9. 如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离为0.7米，顶端距离地面2.4米，如果保持梯子底端位置不动，将梯子斜靠在右墙时，顶端距离地面2米，那么小巷的宽度为（）

A、0.7米 B、1.5米 C、2.2米 D、2.4米

查看试题解析
10. 某同学根据二维码的原理设计了一个方形码的运算：如图，在3×3的正方形网格中，黑色格子表示1，白色格子表示0，每一行都按f（x）＝ax²﹣bx+c进行计算，其中x代表第几行，a代表每一行的第一个格子，b代表每一行的第二个格子，c代表每一行的第三个格子．例如：f（1）＝1×1²﹣0×1+1＝2，f（2）＝0×2²﹣1×2+1＝﹣1，则f（3）的值是（）

A、0 B、2 C、6 D、7

查看试题解析

二、填空题

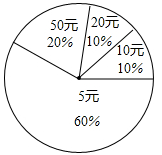
11. 已知 $x = - 1$ 是方程 $a x^{2} + b x + c = 0$ 的根 $(a \neq 0)$ ，则 $a - b + c$ 的值为．

查看试题解析
12. Rt△ABC中，∠C＝90°，D是AB的中点，若AB＝10，则CD的长等于．

查看试题解析
13. 若实数 x ，y满足等式： $y = \sqrt{x - 2} + \sqrt{2 - x} - 2$ ，则xy=

查看试题解析
14. 已知直线 $y = (k - 2) x + k$ 不经过第三象限，则k的取值范围是．

查看试题解析
15. 在一次爱心捐款中，某班有40名学生拿出自己的零花钱，有捐5元、10元、20元、50元的．如图反映了不同捐款的人数比例，那么这个班的学生平均每人捐款元

查看试题解析
16. 四边形具有不稳定性，对于四条边长确定的四边形，当内角度数发生变化时，其形状也会随之改变．如图，改变边长为2的正方形ABCD的内角，变为菱形 $A B C^{'} D^{'}$ ，若 $∠ D^{'} A B = 45 °$ ，则阴影部分的面积是．

查看试题解析

三、解答题

17. 解方程 $x^{2} + 3 x - 4 = 0$ ．

查看试题解析
18. 计算： $(3 + 2 \sqrt{2}) (3 - 2 \sqrt{2}) - \sqrt{54} \div \sqrt{6}$

查看试题解析
19. 小仙骑车从学校回家，中途在十字路口等红灯用了1分钟，然后继续骑车回家．若小仙骑车的速度始终不变，从出发开始计时，小仙离家的距离s（单位：米）与时间t（单位：分钟）的对应关系如图所示，根据图中信息，求小仙骑车的速度及该十字路口与小仙家的距离．

查看试题解析
20. 某篮球队对甲、乙两名运动员进行3分球投篮成绩测试，每天投3分球10次，五天中进球的个数统计结果如下：
队员
第1天
第2天
第3天
第4天
第5天
甲
10
6
10
6
8
乙
7
9
7
8
9
经过计算，甲进球的平均数为8，方差为3.2．

(1)、求乙进球的平均数；

(2)、现在需要根据以上结果，从甲、乙两名队员中选出一人去参加3分球投篮大赛，你认为应该选哪名队员参赛？为什么？

查看试题解析
21. 某农户要利用一面25m长的墙建一个长方形的养鸡场，一边靠墙，另三边用木栅栏围成，木栅栏长40m．

(1)、鸡场的面积能达到 $200 m^{2}$ 吗？如果能，求出与墙平行的边的长；

(2)、鸡场的面积能达到 $210 m^{2}$ 吗？为什么？

查看试题解析
22. 如图，已知菱形ABCD的对角线AC、BD相交于点O ，分别过A、D两点作AO、DO的垂线，两垂线交于点E ．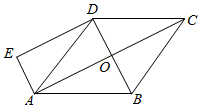

(1)、求证：四边形AODE是矩形；

(2)、若四边形AODE的面积为12，AD＝5，求四边形AODE的周长．

查看试题解析
23. 车厘子与蓝莓深受广大市民喜爱．某水果商看到商机，以车厘子每千克45元，蓝莓每千克20元的价格，购进两种水果共计120千克，并以车厘子每千克52元，蓝莓每千克30元全部售出（不计损耗），设购进车厘子x千克，售出两种水果的利润为y元．

(1)、求y与x之间的关系式；

(2)、若蓝莓的进货量不超过车厘子进货量的3倍，如何进货才能使水果商获得的利润最大，最大利润是多少？

查看试题解析
24. 如图，一次函数 $y_{1} = k x + b (k \neq 0)$ 的图象分别与x轴和y轴相交于C、 $A (0 ， 3)$ 两点，且与正比例函数 $y_{2} = - 2 x$ 的图象交于点 $B (- 1 ， m)$ ．

(1)、求一次函数的解析式；

(2)、当 $y_{1} > y_{2}$ 时，直接写出自变量x的取值范围；

(3)、点D是一次函数图象上一点，若 $S_{△ O C D} = 2 S_{△ O C B}$ ，求点D的坐标．

查看试题解析
25. 如图1，已知在四边形ABCD中，AD∥BC，AB∥CD，BE平分∠ABC，交AD于点E，过点E作EF∥AB，交BC于点F，O是BE的中点，连接OF，OC，OD．

(1)、求证：四边形ABFE是菱形；

(2)、若∠ABC＝90°，如图2所示：
①求证：∠ADO＝∠BCO；
②若∠EOD＝15°，AE＝1，求OC的长．

查看试题解析

队员	第1天	第2天	第3天	第4天	第5天
甲	10	6	10	6	8
乙	7	9	7	8	9