河南省漯河市郾城区2021-2022学年八年级下学期期末数学试卷

试卷更新日期：2022-08-04 类型：期末考试

进入出卷网下载

一、单选题

1. 如果 $\sqrt{(a - 2)^{2}} = 2 - a$ ，那么（）

A、 $a < 2$ B、 $a \leq 2$ C、 $a > 2$ D、 $a \geq 2$

查看试题解析
2. 下列关于一次函数y＝﹣2x＋2的图象的说法中，错误的是（）

A、函数图象经过第一、二、四象限 B、函数图象与x轴的交点坐标为（2，0） C、当x＞0时，y＜2 D、y的值随着x值的增大而减小

查看试题解析

3. 如下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差：

	甲	乙	丙	丁
平均数（cm）	185	180	185	180
方差	2.5	2.5	6.4	7.1

根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

4. 下列关于一次函数y＝﹣2x＋2的图象的说法中，错误的是（）

A、函数图象经过第一、二、四象限 B、函数图象与x轴的交点坐标为（2，0） C、当x＞0时，y＜2 D、y的值随着x值的增大而减小

查看试题解析
5. 如图平行四边形ABCD的周长为20，对角线AC，BD相交于点O，点E是CD的中点，BD＝6，则△DOE的周长为（）

A、6 B、7 C、8 D、10

查看试题解析
6. 已知Rt△ABC中，∠C=90°，若a+b=14cm，c=10cm，则Rt△ABC的面积是( )

A、24cm² B、36cm² C、48cm² D、60cm²

查看试题解析
7. 如图，台阶阶梯每一层高20cm，宽30cm，长50cm，一只蚂蚁从A点爬到B点，最短路程是（）

A、10 $\sqrt{89}$ B、50 $\sqrt{5}$ C、120 D、130

查看试题解析
8. 如图，两张等宽的纸条交叉叠放在一起，若重合部分构成的四边形ABCD中，AB＝3，AC＝2，则四边形ABCD的面积为（）

A、 $4 \sqrt{2}$ B、 $6 \sqrt{2}$ C、 $8 \sqrt{2}$ D、5

查看试题解析
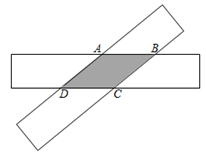9. 如果正整数a、b、c满足等式 $a^{2} + b^{2} = c^{2}$ ，那么正整数a、b、c叫做勾股数.某同学将自己探究勾股数的过程列成下表，观察表中每列数的规律，可知x+y的值为（）

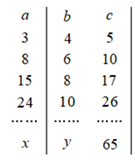A、47 B、62 C、79 D、98

查看试题解析
10.
如图，在矩形ABCD中，对角线AC，BD相交于点O，AE⊥BD，垂足为E，AE=3，ED=3BE，则AB的值为（　　）

A、6 B、5 C、 $2 \sqrt{3}$ D、 $3 \sqrt{3}$

查看试题解析
11.
我们知道：四边形具有不稳定性．如图，在平面直角坐标系中，边长为2的正方形ABCD的边AB在x轴上，AB的中点是坐标原点O，固定点A，B，把正方形沿箭头方向推，使点D落在y轴正半轴上点D′处，则点C的对应点C′的坐标为（）

A、（ $\sqrt{3}$ ，1） B、（2，1） C、（1， $\sqrt{3}$ ） D、（2， $\sqrt{3}$ ）

查看试题解析

二、填空题

12. 计算： $\sqrt{14} \times \sqrt{2}$ ＝.

查看试题解析
13. 一条直线y＝kx＋b与直线y＝－2x＋3平行，且经过点P(2，4)，则该直线的表达式是．

查看试题解析
14. 某中学规定学生体育成绩满分为100分，按课外活动成绩、期中成绩、期末成绩2：3：5的比计算学期成绩．小明同学本学期三项成绩依次为90分、80分、90分，则小明同学本学期的体育成绩是分．

查看试题解析
15. 小高从家门口骑车去单位上班，先走平路到达点A，再走上坡路到达点B，最后走下坡路到达工作单位，所用的时间与路程的关系如图所示．下班后，如果他沿原路返回，且走平路、上坡路、下坡路的速度分别保持和去上班时一致，那么他从单位到家门口需要的时间是分钟．

查看试题解析
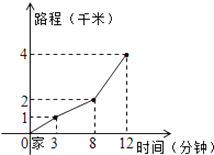16. 在如图所示的平面直角坐标系中，点P是直线y=x上的动点，A（2，0），B（6，0）是x轴上的两点，则PA+PB的最小值为．

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{12} - \sqrt{27} + \sqrt{\frac{1}{3}}$

(2)、 $(2 \sqrt{3} - 1) (2 \sqrt{3} + 1) - {(1 - \sqrt{3})}^{2}$

查看试题解析
18. 已知：如图，直线y₁＝x+1在平面直角坐标系xOy中.

(1)、在平面直角坐标系xOy中画出y₂＝﹣2x+4的图象；

(2)、求y₁与y₂的交点坐标；

(3)、根据图象直接写出当y₁≥y₂时，x的取值范围.

查看试题解析
19. 如图所示的一块地，∠ADC=90°，AD=12m，CD=9m，AB=39m，BC=36m，求这块地的面积．

查看试题解析
20. 某校为了解八年级学生参加社会实践活动情况，随机调查了本校部分八年级学生在第一学期参加社会实践活动的天数，并用得到的数据绘制了统计图①和图②，请根据图中提供的信息，回答下列问题：

(1)、本次接受随机抽样调查的学生人数为，图①中的m的值为；

(2)、求本次抽样调查获取的样本数据的众数、中位数和平均数；

(3)、若该校八年级学生有1200人，估计参加社会实践活动时间大于7天的学生人数．

查看试题解析
21. “端午节小长假”期间，小明一家乘坐高铁前往某市旅游，计划第二天租用新能源汽车自驾出游．
根据以上信息，解答下列问题：

(1)、甲公司每小时的租费是元；

(2)、设租车时间为x小时，租用甲公司的车所需费用为y₁元，租用乙公司的车所需费用为y₂元，分别求出y₁ ， y₂关于x的函数解析式；

(3)、请你帮助小明计算并分析选择哪个出游方案合算．

查看试题解析
22. 端午节前夕，某超市用16800元购进A ， B两种规格的粽子共600件，其中A种规格的进价为每件24元，B种规格的进价为每件36元．

(1)、求购买的A ， B两种规格的粽子各有多少件；

(2)、已知1件A种规格的粽子和1件B种规格的粽子的利润和为20元，且A种规格的粽子利润率不超过50%．设此次销售活动完成后的总利润为w（元），1件A种规格的粽子的利润为a（元）（其中a＞0）．
①求w与a的关系式；

②求w的最大值．

查看试题解析
23. 如图，点A的坐标为 $(0 ， 30)$ ， $∠ A B O = 30 °$ ，点C从点A出发沿AB方向以每秒4个单位长度的速度向点B匀速运动，同时点D从点O出发沿OA方向以每秒2个单位长度的速度向点A匀速运动，设点C、D运动的时间是t秒（ $0 < t < 15$ ）．过点C作 $C E ⊥ B O$ 于点E，连接CD，DE．

(1)、求直线AB的解析式；

(2)、求证：四边形ACED是平行四边形；

(3)、当t为何值时，四边形CEOD的矩形?请直接写出t的值．

查看试题解析
24. 【教材呈现】下图是华师版八年级下册数学教材第121页的部分内容．

(1)、【问题解决】如图①，已知矩形纸片 $A B C D (A B > A D)$ ，将矩形纸片沿过点 $D$ 的直线折叠，使点 $A$ 落在边 $D C$ 上，点 $A$ 的对应点为 $A^{'}$ ，折痕为 $D E$ ，点 $E$ 在 $A B$ 上．求证：四边形 $A E A^{'} D$ 是正方形．

(2)、【规律探索】由【问题解决】可知，图①中的 $Δ A^{'} D E$ 为等腰三角形．现将图①中的点 $A^{'}$ 沿 $D C$ 向右平移至点 $Q$ 处（点 $Q$ 在点 $C$ 的左侧），如图②，折痕为 $P F$ ，点 $F$ 在 $D C$ 上，点 $P$ 在 $A B$ 上，那么 $Δ P Q F$ 还是等腰三角形吗？请说明理由．

(3)、【结论应用】在图②中，当 $Q C = Q P$ 时，将矩形纸片继续折叠如图③，使点 $C$ 与点 $P$ 重合，折痕为 $Q G$ ，点 $G$ 在 $A B$ 上．要使四边形 $P G Q F$ 为菱形，则 $\frac{A D}{A B} =$ ．

查看试题解析