广西壮族自治区来宾市2021-2022学年八年级下学期期末数学试卷
试卷更新日期:2022-08-04 类型:期末考试
一、单选题
-
1. 下列美术字中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、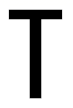 D、
D、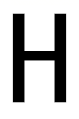
-
2. 在平面直角坐标系中,点关于轴对称的点的坐标是( )A、 B、 C、 D、
-
3. 在下列以线段a、b、c的长为边,能构成直角三角形的是( )A、a=3,b=4,c=6 B、a=5,b=6,c=7 C、a=6,b=8,c=9 D、a=7,b=24,c=25
-
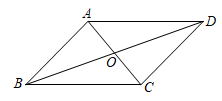
4. 如图,▱ABCD的对角线AC,BD相交于点O,则下列结论一定正确的是( )
 A、OB=OD B、AB=BC C、AC⊥BD D、∠ABD=∠CBD
A、OB=OD B、AB=BC C、AC⊥BD D、∠ABD=∠CBD -
5. 已知直角三角形的两直角边长分别为5和12,则此直角三角形斜边上的中线长为( )A、 B、6 C、13 D、
-
6. 某校对初中学生开展的四项课外活动进行了一次抽样调查(每人只参加其中的一项活动),调查结果如图所示,根据图形所提供的样本数据,可得学生参加科技活动的频率是( )
 A、0.15 B、0.2 C、0.25 D、0.3
A、0.15 B、0.2 C、0.25 D、0.3 -
7. 关于一次函数 , 下列说法正确的是( )A、它的图像经过点 B、它的图像经过第一、二、四象限 C、随的增大而增大 D、当时,
-
8. 如图,在中, , , 平分 , 交于点 , 若 , 则( )
 A、2 B、 C、 D、4
A、2 B、 C、 D、4 -
9. 数经历了从自然数到有理数,到实数,再到复数的发展过程,数学中把形如a+bi(a,b为实数)的数叫做复数,用z=a+bi表示,任何一个复数z=a+bi在平面直角坐标系中都可以用有序数对Z(a,b)表示,如:z=1+2i表示为Z(1,2),则z=2﹣i可表示为( )A、Z(2,0) B、Z(2,﹣1) C、Z(2,1) D、(﹣1,2)
-
10. 如图,△ABC中,AB=AC,点D、E分别是边AB、AC的中点,点G、F在BC边上,四边形DEFG是正方形.若DE=2cm,则AC的长为( )
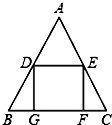 A、 cm B、4cm C、 cm D、2 cm
A、 cm B、4cm C、 cm D、2 cm -
11. 当时,一次函数的图象大致是( )A、
 B、
B、 C、
C、 D、
D、
-
12. 如图,在正方形外取一点 , 连接 , , , 过点作的垂线交于点 , 若 , . 有下列结论:①;②;③点到直线的距离为;④ . 其中正确的结论是( )
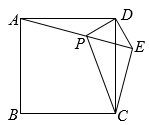 A、①② B、①②③ C、①③④ D、①②④
A、①② B、①②③ C、①③④ D、①②④
二、填空题
-
13. 正五边形每个内角的度数是.
-
14. 函数y=(k+1)x﹣7中,当k满足时,它是一次函数.
-
15. 如图,在菱形中,对角线 , , 则的面积为 .

-
16. 小明用一块含有角()的直角三角尺测量校园内某棵树的高度,示意图如图所示.若小明的眼睛与地面之间的垂直高度为 , 小明与树之间的水平距离为 , 则这棵树的高度约为 . (结果精确到 , 参考数据:)

-
17. 在平面直角坐标系中,在轴,轴上分别截取 , 再分别以点 , 为圆心,以大于长为半径画弧,两弧交于点 , 若点的坐标为 , 则的值是 .
-
18. 如图,在矩形ABCD中,已知AB=2,BC=4,点O、P分别是边AB、AD的中点,点H是边CD上的一个动点,连接OH,将四边形OBCH沿OH折叠,得到四边形OFEH,连接PE,则PE长度的最小值是 .

三、解答题
-
19. 如图,已知▱ABCD的对角线AC、BD相交于点O,AD=12,BD=10,AC=26.
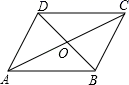 (1)、求△ADO的周长;(2)、求证:△ADO是直角三角形.
(1)、求△ADO的周长;(2)、求证:△ADO是直角三角形. -
20. 某社区为了解居民每月用于信息消费的金额,随机抽取了部分家庭开展问卷调查,并将数据整理成如下的不完整统计图表:
月消费额分组
组别
消费额(元)

请根据以上信息解答下列问题:
(1)、求本次调查样本的容量和组的频数;(2)、补全直方图;(3)、若该社区有2000户住户,请估计月信息消费额少于300元的家庭有多少户. -
21. 如图,已知是的角平分线,且为的中点, , .
 (1)、写出图中所有的全等三角形;(2)、求证: .
(1)、写出图中所有的全等三角形;(2)、求证: . -
22. 如图,在平面直角坐标系中,点的坐标为 .
 (1)、将点向右平移5个单位长度,再向上平移2个单位长度,得到点 , 则点的坐标是;点与点关于原点成中心对称,则点的坐标是;(2)、一次函数的图象经过 , 两点,求直线的函数表达式;(3)、设直线与轴交于点 , 点在轴上,且满足的面积为6,求点的坐标.
(1)、将点向右平移5个单位长度,再向上平移2个单位长度,得到点 , 则点的坐标是;点与点关于原点成中心对称,则点的坐标是;(2)、一次函数的图象经过 , 两点,求直线的函数表达式;(3)、设直线与轴交于点 , 点在轴上,且满足的面积为6,求点的坐标. -
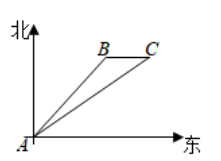
23. 如图,一艘轮船离开 港沿着东北方向直线航行 海里到达 处,然后改变航向,向正东方向航行20海里到达 处,求 的距离.
-
24. 已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
 (1)、求证:△ABM≌△DCM;(2)、当AB:AD的值为多少时,四边形MENF是正方形?请说明理由.
(1)、求证:△ABM≌△DCM;(2)、当AB:AD的值为多少时,四边形MENF是正方形?请说明理由. -
25. 为增加农民收入,助力乡村振兴,某驻村干部指导农户进行草莓种植和销售.已知草莓的种植成本为8元/千克,经市场调查发现,今年五一期间草莓的销售量(千克)与销售单价(元/千克)()满足的函数图象如图所示.
 (1)、根据图象信息,求与的函数表达式();(2)、当草莓的销售单价定为30元/千克时,求草莓的销售量的值;(3)、求当销售单价(元/千克)满足()时销售草莓获得的最大利润.
(1)、根据图象信息,求与的函数表达式();(2)、当草莓的销售单价定为30元/千克时,求草莓的销售量的值;(3)、求当销售单价(元/千克)满足()时销售草莓获得的最大利润. -
26. 如图,直线分别交轴,轴于点 , , 直线交轴于点 , 两直线相交于点 .
 (1)、求点的坐标;(2)、如图2,过点作轴交直线于点 , 连接 , . 求证:四边形是菱形;(3)、如图3,在(2)的条件下,点在线段上,点在线段上,连接 , , 当 , 且时,求点的坐标.
(1)、求点的坐标;(2)、如图2,过点作轴交直线于点 , 连接 , . 求证:四边形是菱形;(3)、如图3,在(2)的条件下,点在线段上,点在线段上,连接 , , 当 , 且时,求点的坐标.
