广西壮族自治区北海市2021-2022学年八年级下学期期末数学试卷

试卷更新日期：2022-08-04 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知一个多边形的内角和是540°，则这个多边形是（）

A、四边形 B、五边形 C、六边形 D、七边形

查看试题解析
3. 已知数据 $\frac{1}{2}$ 、-5、-1.3、π、-2，其中负数出现的频率是（）

A、0.4 B、0.5 C、0.6 D、0.7

查看试题解析
4. 一次函数 $y = 2 x + 3$ 的图象与y轴交点的坐标是（）

A、 $(0 ， - 3)$ B、 $(0 ， 3)$ C、 $(3 ， 0)$ D、 $(- 3 ， 0)$

查看试题解析
5. 如图， $B D$ 平分 $∠ A B C$ ， $D E$ 垂直 $B C$ 于E， $A B = 6$ ， $D E = 3$ ，则 $△ A B D$ 的面积为（）

A、7 B、8 C、9 D、10

查看试题解析
6. 如图，菱形 $A B C D$ 的周长是20， $∠ A = 60 °$ ，则对角线 $B D$ 的长度为（）

A、5 B、 $2 \sqrt{3}$ C、4 D、 $4 \sqrt{3}$

查看试题解析
7. 若三角形三个内角的比为 $1 ： 2 ： 3$ ，则它的最长边与最短边的比为（）

A、 $3 ： 1$ B、 $2 ： 1$ C、 $3 ： 2$ D、 $4 ： 1$

查看试题解析
8. 下列图象中不可能是一次函数 $y = m x - (m - 3)$ 的图象的是（）

A、 B、 C、 D、

查看试题解析
9. 如图，在平面直角坐标系 $x o y$ 中，若菱形 $A B C D$ 的点A，B的坐标分别为 $(- 3 ， 0) ， (2 ， 0)$ ，点D在y轴正方向上，则点C的坐标为（）

A、 $(5 ， 4)$ B、 $(5 ， - 4)$ C、 $(5 ， 4)$ 或 $(5 ， - 4)$ D、不确定

查看试题解析
10. 如图，正方形ABCD中，点E、F、G分别为边AB、BC、AD上的中点，连接AF、DE交于点M，连接GM、CG，CG与DE交于点N，则结论①GM⊥CM；②CD＝DM；③四边形AGCF是平行四边形；④∠CMD＝∠AGM中正确的有（）个．

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 点 $P (- 3 ， 2)$ 关于x轴对称的点 $P^{^{'}}$ 的坐标是．

查看试题解析
12. 已知一组数据有50个，把它分成6组，第1组到第4组的频数分别是10，5，7，8，第5组的频率是0.1，故第6组的频率是．

查看试题解析
13. 如图，已知 $∠ B = ∠ D = 90 °$ ， $B C = D C$ ， $∠ B A C = 40 °$ ，则 $∠ A C D =$ ．

查看试题解析
14. 在平面直角坐标系中，点O是坐标原点，过点A（1，2）的直线y=kx+b与x轴交于点B，且S_△_AOB=4，则k的值是．

查看试题解析
15. 如图，正方形 $A_{1} B_{1} C_{1} O$ ， $A_{2} B_{2} C_{2} C_{1}$ ， $A_{3} B_{3} C_{3} C_{2}$ …按如图所示的方式放置．点 $A_{1} 、 A_{2} 、 A_{3}$ …和点 $C_{1} 、 C_{2} 、 C_{3}$ …分别在直线 $y = k x + b$ （ $k > 0$ 和x轴上，已知点 $B_{1} (1 ， 1) ， B_{2} (3 ， 2)$ ，则 $B_{12}$ 的坐标是．

查看试题解析

三、解答题

16. 已知：如图，DE⊥AB于E，DF⊥AC于F，若BD=CD，BE=CF；求证：AD平分∠BAC．

查看试题解析

17. 某校在“6.26国际禁毒日”前组织八年级全体学生320人进行了一次“毒品预防知识”竞赛，赛后随机抽取了部分学生的成绩进行统计，制作如下频数分布表和频数直方图．请根据表中提供的信息，解答下列问题：

分数段（x表示分数）	频数	频率
$50 \leq x < 60$	4	0.10
$60 \leq x < 70$	8	b
$70 \leq x < 80$	a	0.30
$80 \leq x < 90$	10	0.25
$90 \leq x < 100$	6	0.15

(1)、表中

a =

▲ ，

b =

▲ ，并补全直方图；

(2)、若用扇形统计图描述此成绩统计分布表，则分数段

60 \leq x < 70

对应扇形的圆心角度数是．

(3)、请估计该年级分数在

80 \leq x < 100

的学生有多少人？

查看试题解析

18. $Δ A B C$ 在平面直角坐标系 $x O y$ 中的位置如图所示， $Δ A B C$ 的顶点均在格点上，且点 $A$ 的坐标是 $(- 2 ， - 2)$ .

(1)、直接写出点 $B$ 和点 $C$ 的坐标；

(2)、把 $Δ A B C$ 向上平移 $3$ 个单位，再向右移 $2$ 个单位得到 $Δ A_{1} B_{1} C_{1}$ ，画出 $Δ A_{1} B_{1} C_{1}$ ，并写出点 $B_{1}$ 的坐标.

查看试题解析
19. 一艘船以40km/s的速度向正东航行，在A处测得灯塔C在北偏东60°方向上继续航行1h.到达B处，这时测得灯塔C在北偏东30°方向上，已知在灯塔C的四周30 km内有暗礁，问这船继续向东航行是否安全？

查看试题解析
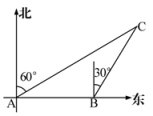20. 如图，等腰 $△ A B C$ 中， $A B = A C$ ， $A D ⊥ B C$ 交 $B C$ 于D点，E点是 $A B$ 的中点，分别过D、E两点作线段 $A C$ 的垂线，垂足分别为G、F两点．

(1)、求证：四边形 $D E F G$ 为矩形；

(2)、若 $A B = 10$ ， $E F = 4$ ，求 $B C$ 的长．

查看试题解析
21. 抗击疫情，我们在行动．某药店销售A型和B型两种型号的口罩，销售一箱A型口罩可获利120元，销售一箱B型口罩可获利140元．该药店计划一次购进两种型号的口罩共100箱，其中B型口罩的进货量不超过A型口罩的3倍．设购进A型口罩x箱，这100箱口罩的销售总利润为y元．

(1)、求y与x的函数关系式；

(2)、该商店购进A型、B型口罩各多少箱，才能使销售利润最大？最大利润是多少？

(3)、若限定该药店最多购进A型口罩70箱，则这100箱口罩的销售总利润能否为12500元？请说明理由．

查看试题解析
22. 已知正方形ABCD，点P是对角线AC所在直线上的动点，点E在DC边所在直线上，且随着点P的运动而运动，PE=PD总成立。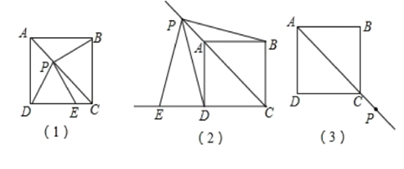

(1)、如图(1)，当点P在对角线AC上时，请你通过测量、观察，猜想PE与PB有怎样的关系?(直接写出结论不必证明)；

(2)、如图(2)，当点P运动到CA的延长线上时，(1)中猜想的结论是否成立?如果成立，请给出证明；如果不成立，请说明理由；

(3)、如图(3)，当点P运动到CA的反向延长线上时，请你利用图(3)画出满足条件的图形，并判断此时PE与PB有怎样的关系?(直接写出结论不必证明)

查看试题解析
23. 当m，n是非零实数，且满足 $4 m - 6 n = 3 m n$ 时，就称点 $P (m ， \frac{m}{n})$ 为“完美点”．

(1)、若点M为“完美点”，且横坐标为2，则点M的纵坐标为；

(2)、“完美点”P在直线（填直线解析式）上；

(3)、如图，已知点 $A (3 ， 0) ， B (0 ， 4) ， C (0 ， \frac{3}{2})$ ，直线 $A B$ 上的“完美点”为点E．连接 $C E$ ， $A C$ ．
①求 $△ C B E$ 的面积；
②在平面直角坐标系中，是否存在点F，使得以点B，C，E，F为顶点的四边形是平行四边形，如果存在，请求出点F的坐标；如果不存在，请说明理由．

查看试题解析