广西壮族自治区百色市靖西市2021-2022学年八年级下学期期末数学试卷

试卷更新日期：2022-08-04 类型：期末考试

进入出卷网下载

一、单选题

1. 一个七边形的内角和度数为（）

A、360° B、720° C、900° D、1080°

查看试题解析
2. 数字“20220705”中，数字“2”出现的频数是（）

A、1 B、2 C、3 D、4

查看试题解析
3. 将一元二次方程 $3 x^{2} - 1 = 5 x$ 化为一般形式后，其中二次项系数、一次项系数、常数项分别是（）

A、 $3 ， 5 ， - 1$ B、 $- 3 ， 5 ， 1$ C、 $3 ， - 5 ， - 1$ D、 $3 ， - 5 ， 1$

查看试题解析
4. 在实数范围内要使 $\sqrt{{(a - 2)}^{2}} = a - 2$ 成立，则a的取值范围是（　　　）

A、a=2 B、 $a > 2$ C、 $a \geq 2$ D、 $a \leq 2$

查看试题解析
5. 在方差计算公式s² $= \frac{1}{20}$ [（x₁﹣15）²+（x₂﹣15）²+…+（x₂₀﹣15）²]中，可以看出15表示这组数据的（）

A、众数 B、平均数 C、中位数 D、方差

查看试题解析
6. 下列计算正确的是（）

A、 $\sqrt{3} + \sqrt{7} = \sqrt{10}$ B、 $2 + \sqrt{2} = 2 \sqrt{2}$ C、 $\sqrt{3} \times \sqrt{6} = 3 \sqrt{2}$ D、 $\sqrt{15} \div \sqrt{5} = 3$

查看试题解析
7. 方程x（x﹣2）＝x的根是（）

A、x＝0 B、x＝2 C、x₁＝0，x₂＝2 D、x₁＝0，x₂＝3

查看试题解析
8. 在 $△ A B C$ 中，若 $A C^{2} - B C^{2} = A B^{2}$ ，则（）

A、 $∠ A = 90 °$ B、 $∠ B = 90 °$ C、 $∠ C = 90 °$ D、不能确定

查看试题解析
9. 如图是某组15名学生数学测试成绩的频数分布直方图，则成绩低于60分的人数是（）

A、3人 B、6人 C、10人 D、14人

查看试题解析
10. 矩形、菱形、正方形都具有的性质是（）

A、对角互补 B、对角线互相垂直 C、对角线互相平分 D、四边相等

查看试题解析
11. 勾股定理是历史上第一个把数与形联系起来的定理，其证明是论证几何的发端．下面四幅图中不能证明勾股定理的是（）

A、 B、 C、 D、

查看试题解析
12. 如图，O是矩形ABCD的对角线BD的中点，E是AB边的中点．若AB＝12，OE＝ $\frac{5}{2}$ ，则线段OC的长为（）

A、3 B、4 C、5.5 D、6.5

查看试题解析

二、填空题

13. 五边形从某一个顶点出发可以引条对角线．

查看试题解析
14. 某校7名同学的体能监测成绩（单位：分）如下：50，49，47，49，47，50，47，则7名同学体能监测成绩的众数是．

查看试题解析
15. 一元二次方程x²﹣2x+1＝0的两个实数根为α，β，则α+β+α•β＝.

查看试题解析
16. 某班50位同学中，1月份出生的频率是0.20，这个班1月份出生的同学有人．

查看试题解析
17. 若二次根式 $\sqrt{2 x + 7}$ 是最简二次根式，则x可取的最小整数是．

查看试题解析
18. 如图，平行四边形ABCD中，AB＝5，AD＝7，∠BAD和∠ADC的平分线交BC于E、F两点，则EF的长是．

查看试题解析

三、解答题

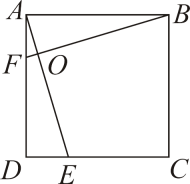
19. 计算： $(\sqrt{3} + 2) (\sqrt{3} - 2) + \sqrt{8} - \sqrt{\frac{9}{2}}$ ．

查看试题解析
20. 已知关于x的一元二次方程x²+（2k+2）x+k²+2k＝0．求证：无论k为何值，方程总有两个不相等的实数根．

查看试题解析
21. 如图，在正方形ABCD中，AE、BF相交于点O且AF＝DE．求证：∠DAE＝∠ABF．

查看试题解析
22. 某学校从九年级同学中任意选取40人，平均分成甲、乙两个小组进行“引体向上”体能测试，根据测试成绩绘制出如下的统计表和统计图（成绩均为整数，满分为10分）．
甲组成绩统计表
成绩
7
8
9
10
人数
1
9
7
3
请根据上面的信息，解答下列问题：

(1)、m＝，乙组成绩的中位数是；

(2)、已知乙组成绩的方差 $s_{乙}^{2} = 0.75$ ，求出甲组成绩的方差，并判断哪个小组的成绩更加稳定？

查看试题解析
23. 如图，平行四边形ABCD中，对角线AC、BD相交于点O，AB⊥AC，AB＝6，AD＝10，求BD的长．

查看试题解析
24. 某商场一月份的销售额为125万元，二月份的销售额下降了20%，商场从三月份起加强管理，改善经营，使销售额稳步上升，四月份的销售额达到了169万元．

(1)、求二月份的销售额；

(2)、求三、四月份销售额的平均增长率．

查看试题解析
25. 我市七年级学生举行了“防溺水”安全知识竞赛，为了了解本次竞赛成绩情况，从中随机抽取了部分参赛学生的成绩（满分100分，得分均为正整数且无满分，最低分为75分），将所抽成绩进行分析统计，并绘制如下频率分布表和尚不完整的频数分布直方图．
请根据图表提供的信息，解答下列问题：
分组
分数段
频数
频率
A
74.5～79.5
24
0.05
B
79.5～84.5
72
m
C
84.5～89.5
168
0.35
D
89.5～94.5
n
0.25
E
94.5～99.5
96
0.20

(1)、本次抽取的样本容量为， m＝， n＝；

(2)、将频数分布直方图补充完整；

(3)、若成绩在89.5分以上定为优秀，据此推测，我市8000名参赛学生中成绩为优秀的学生约有多少名？

查看试题解析
26. 如图，在▱ABCD中，DB⊥CB．

(1)、延长CB到E，使BE＝CB，连接AE，求证：四边形AEBD是矩形；

(2)、若点F，G分别是AB，CD的中点，连接DF、BG，试判断四边形DFBG是什么特殊的四边形？并证明你的结论．

查看试题解析

分组	分数段	频数	频率
A	74.5～79.5	24	0.05
B	79.5～84.5	72	m
C	84.5～89.5	168	0.35
D	89.5～94.5	n	0.25
E	94.5～99.5	96	0.20

成绩	7	8	9	10
人数	1	9	7	3