福建省泉州市洛江区2021-2022学年八年级下学期期末数学试卷

试卷更新日期：2022-08-04 类型：期末考试

进入出卷网下载

一、单选题

1. 使分式 $\frac{x}{2 x- 4}$ 有意义的x的取值范围是（）

A、x=2 B、x≠2且x≠0 C、x=0 D、x≠2

查看试题解析
2. 点 $P (- 5 ， 3)$ 关于 $x$ 轴对称点 $P_{1}$ 的坐标为（）

A、 $(- 5 ， - 3)$ B、 $(5 ， 3)$ C、 $(5 ， - 3)$ D、 $(3 ， - 5)$

查看试题解析
3. 某种细胞的直径是 $5 \times 1 0^{- 4}$ 毫米，这个数用小数表示是（）

A、0.00005 B、0.0005 C、-50000 D、50000

查看试题解析
4. 如图为某队员射击10次的成绩统计图，该队员射击成绩的众数与中位数分别是（）

A、8，7 B、7，6.5 C、7，7 D、8，7.5

查看试题解析
5. 在▱ABCD中，∠A=3∠B，则∠B的度数是（）

A、30° B、36° C、45° D、60°

查看试题解析
6. 下列说法错误的是（）

A、平行四边形的对边相等 B、对角线相等的四边形是矩形 C、对角线互相垂直的平行四边形是菱形 D、正方形既是轴对称图形、又是中心对称图形

查看试题解析
7. 如图，矩形 $A B C D$ 的两条对角线相交于点 $O$ ，已知 $∠ A O D = 120 °$ ， $A B = 2.5 c m$ ，则矩形对角线 $B D$ 的长为（）

A、 $3 c m$ B、 $4 c m$ C、 $5 c m$ D、 $6 c m$

查看试题解析
8. 如图，菱形 $A B C D$ 对角线 $A C = 8 c m$ ， $B D = 6 cm$ ，则菱形高 $D E$ 长为（）

A、 $5 c m$ B、 $10 c m$ C、 $4.8 c m$ D、 $9.6 c m$

查看试题解析
9. 若点 $A (- 5 ， y_{1})$ 、 $B (- 3 ， y_{2})$ 、 $C (2 ， y_{3})$ 在反比例函数 $y = - \frac{5}{x}$ 的图象上，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小关系是（）

A、 $y_{3} < y_{1} < y_{2}$ B、 $y_{2} < y_{1} < y_{3}$ C、 $y_{3} < y_{2} < y_{1}$ D、 $y_{1} < y_{2} < y_{3}$

查看试题解析
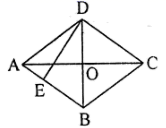10. 如图，一直线与两坐标轴的正半轴分别交于 $A$ 、 $B$ 两点， $P$ 是线段 $A B$ 上任意一点（不包括端点），过点 $P$ 分别作两坐标轴的垂线，与两坐标轴围成的矩形的周长为4，则线段 $O P$ 的最小值为（）

A、 $\frac{\sqrt{2}}{2}$ B、1 C、 $\sqrt{2}$ D、2

查看试题解析

二、填空题

11. 计算： ${(- 3)}^{0} + {(\frac{1}{2})}^{- 1} =$ ．

查看试题解析
12. 如图，在矩形 $A B C D$ 中， $A E$ 平分 $∠ B A D$ 交 $B C$ 于点 $E$ ， $A D = 8 c m$ ， $C E = 3 c m$ ，则 $A B =$ $c m$ ．

查看试题解析
13. 某种数据方差的计算公式是 $S^{2} = \frac{1}{8} [{(x_{1} - 4)}^{2} + {(x_{2} - 4)}^{2} + \dots + {(x_{a} - 4)}^{2}]$ ，则该组数据的总和为．

查看试题解析
14. 如图，在平面直角坐标系中，若ABCD的顶点A，B，C的坐标分别是 $(3 ， 4) ， (1 ， - 1) ， (7 ， - 1)$ ，则点D的坐标是＝．

查看试题解析
15. 已知一次函数 $y_{1} = a x + b$ 与反比例函数 $y_{2} = \frac{k}{x}$ 的图象如图所示．在第一象限内，当 $y_{1} > y_{2}$ 时，则 $x$ 的取值范围是．

查看试题解析
16. 如图，正方形 $A B C D$ 中，点 $E$ 是 $A D$ 边的中点， $B D$ 、 $C E$ 交于点 $H$ ， $B E$ 、 $A H$ 交于点 $G$ ，则下列结论：① $∠ B C E = 60 °$ ；② $A G ⊥ B E$ ；③ $S_{△ B H E} = S_{△ C H D}$ ；④ $∠ A H B = ∠ E H D$ ．其中正确的序号是．

查看试题解析

三、解答题

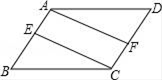
17. 先化简，后求值： $(1 + \frac{1}{x - 1}) \div \frac{x}{x^{2} - 1}$ ，其中x=-2.

查看试题解析
18. 如图，在平行四边形ABCD中，AE=CF，求证：AF=CE．

查看试题解析
19. 某中学八年级(1)班共40名同学开展了“献爱心”的活动．活动结束后，生活委员小林将捐款情况进行了统计，并绘制成如图所示的统计图．

(1)、求这40名同学捐款的平均数；

(2)、该校共有学生1200名，请根据该班的捐款情况，估计这个中学的捐款总数大约是多少元?

查看试题解析
20. 已知直线 $l_{1}$ 和 $l_{2}$ 的表达式分别为 $y = - 2 x + 1$ 和 $y = k x + 6$ ，这两条直线相交于点 $A (- 1 ， a)$ ．

(1)、求 $a$ 和 $k$ 的值；

(2)、若直线 $l_{3}$ 的表达式为 $y = 5 x + 8$ ，试说明：直线 $l_{1}$ ， $l_{2}$ ， $l_{3}$ 相交于同一个点．

查看试题解析
21. 已知：矩形 $A B C D$ ．

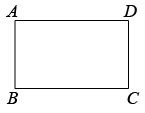(1)、在线段 $B C$ 上求作点 $E$ ，使得 $∠ A E B = ∠ A E D$ ；（要求：尺规作图，保留作图痕迹，不写作法）

(2)、在（1）的条件下，若 $D C = 3$ ， $A D = 5$ ，求 $B E$ 的长．

查看试题解析
22. 现有A，B两种商品，已知买一件A商品比买一件B商品少20元，用210元全部购买A商品的数量与用350元全部购买B商品的数量相同．

(1)、A，B两种商品每件各是多少元？

(2)、如果要购买A，B两种商品共10件，总费用不超过400元，且不低于370元，那么一共有几种购买方案？

查看试题解析
23. 甲乙两人分别开汽车和骑自行车沿着相同的路线同时从 $A$ 地出发驶往 $B$ 地，甲到达 $B$ 地后休息一段时间原路返回 $A$ 地．他们离 $A$ 地的距离 $y (k m)$ 随时间 $x (h)$ 的变化如下图所示，请根据图中提供的信息，解决下列问题：

(1)、 $A B$ 两地相距 $k m$ ，去 $B$ 地时甲的速度为 $k m / h$ ，乙的速度为 $k m / h$ ；

(2)、若甲返回时在离 $B$ 地12.5千米处与乙相遇，求图中线段 $M N$ 的解析式，并写出 $x$ 的范围；

(3)、整个行程中，当 $x$ 为何值时，甲乙之间的距离恰好是5千米？

查看试题解析
24. 如图在正方形ABCD中，点F在CD延长线上，点E在BC边上，且BE=DF，连接EF交对线BD与点G，连接AE，AF，AG．

(1)、求证：AE=AF．

(2)、求证：BG-DG= $\sqrt{2}$ DF．

(3)、若DG=4，DF= $\sqrt{2}$ ，直接写出正方形ABCD的边长= ．

查看试题解析
25. 已知：如图1，点 $A (4 ， n)$ 是反比例函数 $y = \frac{8}{x} (x > 0)$ 图象上的一点．

(1)、求 $n$ 的值和直线 $O A$ 的解析式；

(2)、如图2，将反比例函数 $y = \frac{8}{x} (x > 0)$ 的图象绕原点 $O$ 逆时针旋转 $45 °$ 后，与 $y$ 轴交于点 $M$ ，求线段 $O M$ 的长度；

(3)、如图3，将直线 $O A$ 绕原点 $O$ 逆时针旋转 $45 °$ ，与反比例函数 $y = \frac{8}{x} (x > 0)$ 的图象交于点 $B$ ，求点 $B$ 的坐标．

查看试题解析