江苏省扬州市江都区2021-2022学年七年级下学期期末数学试卷
试卷更新日期:2022-08-04 类型:期末考试
一、单选题
-
1. 若a>b,则下列结论错误的是( )A、a-3>b-3 B、a+3>b+3 C、3a>3b D、3-a>3-b2. 下列各式从左到右的变形属于因式分解的是( ).A、 B、 C、 D、3. 下图能说明∠1>∠2的是( )A、
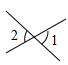 B、
B、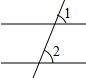 C、
C、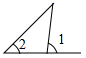 D、
D、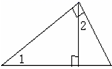 4. 我们知道,借助图形可以验证公式.下列图形可以用来验证平方差公式a2−b2=(a+b)(a−b)的是( )A、
4. 我们知道,借助图形可以验证公式.下列图形可以用来验证平方差公式a2−b2=(a+b)(a−b)的是( )A、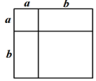 B、
B、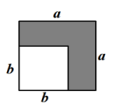 C、
C、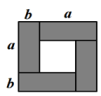 D、
D、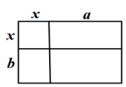 5. 下列命题中,属于真命题的是( )A、如果 , 那么 B、如果 , 那么 C、如果 , 那么 D、如果 , 那么6. 班级要用40元钱买A、B两种型号的口罩,两种型号口罩必须都买,已知A型口罩每个6元,B型口罩每个4元,在钱全部用尽的情况下,购买方案有( )A、2种 B、3种 C、4种 D、5种7. 被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作.《九章算术》中记载:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”译文:“今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕每只各重多少斤?”设每只雀重x斤,每只燕重y斤,可列方程组为( )A、 B、 C、 D、8. 若关于x的不等式组恰有三个整数解,则a的取值范围是( )A、-2<a<- 1 B、-2≤a<- 1 C、-2<a≤ - 1 D、-2≤a≤- 1
5. 下列命题中,属于真命题的是( )A、如果 , 那么 B、如果 , 那么 C、如果 , 那么 D、如果 , 那么6. 班级要用40元钱买A、B两种型号的口罩,两种型号口罩必须都买,已知A型口罩每个6元,B型口罩每个4元,在钱全部用尽的情况下,购买方案有( )A、2种 B、3种 C、4种 D、5种7. 被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作.《九章算术》中记载:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”译文:“今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀、6只燕重量为1斤.问雀、燕每只各重多少斤?”设每只雀重x斤,每只燕重y斤,可列方程组为( )A、 B、 C、 D、8. 若关于x的不等式组恰有三个整数解,则a的取值范围是( )A、-2<a<- 1 B、-2≤a<- 1 C、-2<a≤ - 1 D、-2≤a≤- 1二、填空题
-
9. 2019冠状病毒(2019-nCoV)是目前已知的第7种可以感染人的冠状病毒,病毒颗粒的平均直径约为98纳米.已知1纳米米,则98纳米用科学记数法表示为米.10. 计算:的结果是 .11. 若 ,则 的值为.12. 已知 , , 则 .13. 已知 , ,则 .14. 我们把各边相等,且各角也相等的多边形叫做正多边形,如图,边长相等的正五边形和正方形的一边重合,则°.
 15. 如图,把一张长方形纸条ABCD沿EF折叠. 若 , 则°.
15. 如图,把一张长方形纸条ABCD沿EF折叠. 若 , 则°. 16. 观察:第1个等式 , 第2个等式 , 第3个等式 , 第4个等式…猜想:第n个等式是.17. 一个三角形的周长为10cm,其中两边长分别是xcm、(2x-1)cm,则x的取值范围是.18. 规定 , 若x、y满足 , , 则x的取值范围是.
16. 观察:第1个等式 , 第2个等式 , 第3个等式 , 第4个等式…猜想:第n个等式是.17. 一个三角形的周长为10cm,其中两边长分别是xcm、(2x-1)cm,则x的取值范围是.18. 规定 , 若x、y满足 , , 则x的取值范围是.三、解答题
-
19. 计算:(1)、(2)、20. 因式分解:(1)、(2)、21. 先化简,再求值: , 其中x,y满足 .22. 解方程组:(1)、(2)、23. 解下列不等式(组)(1)、解不等式 , 并把它的解集在数轴上表示出来.(2)、解不等式组24. 已知:如图1,AD∥BC,∠ABC=∠ADC,求证:AB∥CD.
 (1)、请补充下面证明过程
(1)、请补充下面证明过程证明:∵AD∥BC(已知)
∴∠ ▲ +∠ABC =180°( )
∵∠ABC=∠ADC(已知)
∴∠ ▲ ∠ADC =180°( )
∴AB∥CD( )
(2)、某同学想到了另一种证法,请你补充完整他的证明过程.证明:连接BD,如图2.
25. 若关于x,y的方程组(m为常数).(1)、解这个方程组(用含m的代数式表示);(2)、是否存在整数m,使方程组的解满足x为负数,y为非正数?若存在,请求出m的值;若不存在,请说明理由.26. 为了加强公民的节水意识,合理利用水资源.某市采用阶梯价格调控手段达到节水目的,价目表如图. (1)、若某户居民1月份用水8 m3 , 则水费元;(2)、若某户居民某月用水x m3 , 则用含x的代数式表示水费;(3)、若某户居民3、4月份共用水15 m3 , (4月份用水量超过3月份),共交水费44元,则该户居民3、4月份各用水多少立方米?27. 某数学实验小组在探究“关于x的二次三项式ax2+bx+3的性质(a、b为常数)”时,进行了如下活动.
(1)、若某户居民1月份用水8 m3 , 则水费元;(2)、若某户居民某月用水x m3 , 则用含x的代数式表示水费;(3)、若某户居民3、4月份共用水15 m3 , (4月份用水量超过3月份),共交水费44元,则该户居民3、4月份各用水多少立方米?27. 某数学实验小组在探究“关于x的二次三项式ax2+bx+3的性质(a、b为常数)”时,进行了如下活动.【实验操作】取不同的x的值,计算代数式ax2+bx+3的值.
x
…
﹣1
0
1
2
3
…
ax2+bx+3
…
0
3
4
…
(1)、根据上表,计算出a、b的值,并补充完整表格.(2)、【观察猜想】实验小组组员,观察表格,提出以下猜想.同学甲说:“代数式ax2+bx+3的值随着x的增大而增大”.同学乙说:“不论x取何值,代数式ax2+bx+3的值一定不大于4”.
请你也提出一个合理的猜想:
(3)、【验证猜想】我们知道,猜想有可能是正确的,也可能是错误的.
请你分别判断甲、乙两位同学的猜想是否正确,若不正确,请举出反例;若正确,请加以说理.28. 在△ABC中,BD平分∠ABC交AC于点D,点E是线段AC上的动点(不与点D重合),过点E作EFBC交射线BD于点F,∠CEF的角平分线所在直线与射线BD交于点G. (1)、如图1,点E在线段AD上运动.
(1)、如图1,点E在线段AD上运动.①若∠ABC=30°,∠C=70°,则∠BGE= ▲ °;
②若∠A=60°,则∠BGE= ▲ °;
③探究∠BGE与∠A之间的数量关系,并说明理由;
(2)、若点E在线段DC上运动时,直接写出∠BGE与∠A之间的数量关系.