湖南省怀化市新晃县2021-2022学年七年级下学期期末质量检测数学试卷（乡镇）

试卷更新日期：2022-08-04 类型：期末考试

进入出卷网下载

一、单选题

1. 计算 $- x^{2} \cdot x$ 的结果是（）

A、 $x^{2}$ B、 $- x^{2}$ C、 $x^{3}$ D、 $- x^{3}$

查看试题解析
2. 方程组 ${\begin{array}{l} 3 x + y = 17 \\ x + y = 7 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 2 \\ y = 5 \end{array}$ B、 ${\begin{array}{l} x = 5 \\ y = 2 \end{array}$ C、 ${\begin{array}{l} x = 6 \\ y = 1 \end{array}$ D、 ${\begin{array}{l} x = 8 \\ y = - 1 \end{array}$

查看试题解析
3. 计算 $(x - 1)^{2}$ 的正确结果是（）

A、 $x^{2} + 1$ B、 $x^{2} - 1$ C、 $x^{2} - 2 x + 1$ D、 $x^{2} + 2 x + 1$

查看试题解析
4. 下列多项式能分解因式的是（）

A、 $x^{2} + y^{2}$ B、 $x^{2} - x y + x$ C、 $x^{2} + 2 x y - y^{2}$ D、 $x^{2} - 8$

查看试题解析
5. 下列统计量中，表示一组数据波动程度的量是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
6. 下面四个图形分别是绿色食品节水、节能和回收标志，在这四个标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
7. 下列四个说法中，正确的是（）

A、内错角相等 B、对顶角相等 C、平移改变图形的形状 D、旋转改变图形的大小

查看试题解析
8. 如图，直线AB、CD相交于点O，OE⊥AB，O为垂足，如果∠EOD＝38°，下列结论不正确的是（）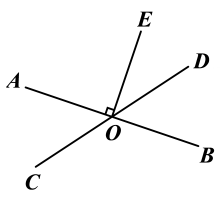

A、∠EOB=90° B、∠DOB是∠AOE 的补角 C、∠AOC=52° D、∠AOC与∠EOD 互为余角

查看试题解析
9. 若 $x + y = 2$ ， $x y = - 2$ ，则 $(1 - x) (1 - y)$ 的值是（）

A、 $- 1$ B、 $1$ C、 $5$ D、 $- 3$ .

查看试题解析
10. 如图， $A B ∥ D C$ ， ∠ADC=∠ABC，DE平分∠ADC，BF平分∠ABC，则下列结论：①∠2=∠3，②∠2=∠6，③∠1=∠6，④∠2=∠5，⑤∠4=∠6，其中正确的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 计算： $(- 2 x y^{2})^{2}$ = ．

查看试题解析
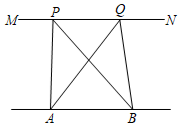
12. 分解因式： $2 x^{2} y - 4 y$ = ．

查看试题解析
13. 已知方程2x﹣y＝1，用含x的代数式表示y，得．

查看试题解析
14. 若 $x^{2} + k x + 16$ 是一个完全平方式，则k= ．

查看试题解析
15. 六名同学在“爱心捐助”活动中，捐款数额为8，10，9，10，4，6（单位：元），这组数据的中位数是．

查看试题解析
16. 如图， $M N / / A B$ ， $P$ ， $Q$ 为直线 $M N$ 上的任意两点，则 $S_{△ P A B}$ $S_{△ Q A B}$ （用“ $>$ ， $=$ ， $<$ ”填写）

查看试题解析

三、解答题

17. 计算：

(1)、 $8 x y \cdot (- \frac{1}{4} x y^{2})$

(2)、 $(2 x - y)^{2} - 4 x (x - y)$

查看试题解析
18. 因式分解：

(1)、 $x^{2} y^{3} - y^{5}$

(2)、 $x (x - y) + y (y - x)$

查看试题解析
19. 解下列方程组：

(1)、 ${\begin{array}{l} x + y = 7 \\ 3 x - y = 5 \end{array}$

(2)、 ${\begin{array}{l} \frac{x}{5} - \frac{y}{2} = 2 \\ 2 (x - 2) + 3 y = 0 \end{array}$

查看试题解析
20. 探究：如图，直线 $A B$ 、 $B C$ 、 $A C$ 两两相交，交点分别为点 $A$ 、 $B$ 、 $C$ ，点 $D$ 在线段 $A B$ 上，过点 $D$ 作 $D E / / B C$ 交 $A C$ 于点 $E$ ，过点 $E$ 作 $E F / / A B$ 交 $B C$ 于点 $F$ ．若 $∠ A B C = 58 °$ ，求 $∠ D E F$ 的度数．
请将下面的解答过程补充完整，并填空（理由或数学式）
解：∵ $D E / / B C$ ， ∴ $∠ D E F =$   ▲   ．（  ）
∵ $E F / / A B$ ， ∴  ▲   $= ∠ A B C$ ．（  ）
∴ $∠ D E F = ∠ A B C$ ．（等量代换）
∵ $∠ A B C = 58 °$ ， ∴ $∠ D E F =$   ▲  °．

查看试题解析
21. 如图，方格纸上每个小方格的边长都是1，观察图形，解答下列问题：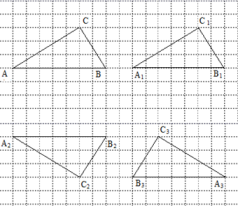

（1）△A₁B₁C₁由△ABC如何变换得来？
（2）△ABC作轴对称变换能否得到△A₂B₂C₂？若能，请画出对称轴MN；若不能，请简要说明理由．
（3）怎样把△ABC变换成△A₃B₃C₃？请写出变换过程．

查看试题解析
22. 在一次中学生田径运动会上，根据参加男子跳高初赛的运动员的成绩（单位： $m$ ），绘制出如下统计图①和②．请根据相关信息，解答下列问题：

(1)、图①中 $a$ 的值为．

(2)、求参加男子跳高初赛的人数．

(3)、求统计的这组初赛数据的平均数、众数．

(4)、根据这组初赛成绩，由高到低确定9人能进行复赛，请直接写出初赛成绩为1.60m的运动员能否进入复赛．

查看试题解析
23. 放学后，小贤和小艺来到学校附近的地摊上购买一种特殊型号的笔芯和卡通笔记本，这种笔芯每盒10支，如果整盒买比单支买每支可优惠0.5元，小贤要买3支笔芯，2本笔记本需花19元，小艺要买7支笔芯，1本笔记本需花费26元．

(1)、求笔记本的单价和单独购买一支笔芯的价格；

(2)、小贤和小艺都还想再买一件单价为3元的小工艺品，但如果他们各自为要买的文具付款后，只有小贤还剩2元钱，他们要怎样做才能既买到各自的文具，又都买到小工艺品，请通过运算说明．

查看试题解析
24. 如图，O是直线AB上的点，E、C、F在同一直线上，且OE、OF分别是∠AOC和∠BOC的平分线，OD⊥EF，垂足为D．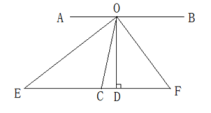

(1)、OE与OF有什么关系？试说明理由．

(2)、若OF=6，OE=8，EF=10，求OD的长．

(3)、若∠AOE=35°，∠F=55°，AB与EF是否平行？请说明理由．

查看试题解析