湖北省咸宁市通城县2021-2022学年七年级下学期期末数学试卷

试卷更新日期：2022-08-04 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数中，最大的一个数是（）

A、-5 B、 $- \sqrt{3}$ C、 $π$ D、 $\sqrt{6}$

查看试题解析
2. 下列图案中，能通过左边的图案平移得到的是（）

A、 B、 C、 D、

查看试题解析
3. 点（9， $- 5$ ）位于平面直角坐标系中的（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 如图，直线 $a / / b$ ，等腰直角三角形的两个顶点分别落在直线 $a$ 、 $b$ 上，若 $∠ 1 = 30^{\circ}$ ，则 $∠ 2$ 的度数是（）

A、 $45^{\circ}$ B、 $30^{\circ}$ C、 $15^{\circ}$ D、 $10^{\circ}$

查看试题解析
5. 以下条件中，不能判断图中 $A B / / C D$ 的是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ 2 = ∠ 4$ C、 $∠ 1 = ∠ A$ D、 $∠ 2 + ∠ 3 = 18 0^{°}$

查看试题解析
6. 点P的坐标是（2-a，3a+6），且点P到两坐标轴的距离相等，则点P坐标是（）

A、（3， 3） B、（3，-3） C、（6，-6） D、（3，3）或 $(6 ， - 6)$

查看试题解析
7. 下列选项中，显示部分在总体中所占百分比的统计图是（）

A、扇形统计图 B、条形统计图 C、折线统计图 D、直方图

查看试题解析
8. 某年级学生共有246人，其中男生人数y比女生人数x的2倍少2人，则下面所列的方程组中符合题意的有（）

A、 ${\begin{matrix} x + y = 246 \\ 2 y = x - 2 \end{matrix}$ B、 ${\begin{matrix} x + y = 246 \\ 2 x = y + 2 \end{matrix}$ C、 ${\begin{matrix} x + y = 216 \\ y = 2 x + 2 \end{matrix}$ D、 ${\begin{matrix} x + y = 246 \\ 2 y = x + 2 \end{matrix}$

查看试题解析

二、填空题

9. 已知 ${\begin{array}{l} x = - 2 \\ y = 2 \end{array}$ 是方程 $k x + 2 y = - 8$ 的解，则 $k =$ .

查看试题解析
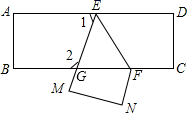
10. 在平面直角坐标系中，若点 $M (1 ， 3)$ 与点 $N (x ， 3)$ 的距离是8，则 $x$ 的值是

查看试题解析
11. 若 ${(a - 2)}^{2} + \sqrt{b + 1} = 0$ ．则b+a＝．

查看试题解析
12. 如图，把一张长方形纸片ABCD沿EF折叠后，D、C分别在M、N的位置上，EM与BC的交点为G，若∠EFG＝65°，则∠2＝．

查看试题解析
13. 如图，写出一个能判定AD∥BC的条件：．

查看试题解析
14. 如图， $Δ A B C$ 沿直线 $A B$ 向下平移可以得到 $Δ D E F$ ，如果 $A B = 8 ， B D = 5$ ，那么 $B E$ 等于.

查看试题解析
15. 若 $x^{3 m - n}$ － $2 y^{n - 1}$ $= 5$ 是二元一次方程，则 $m + n$ = ．

查看试题解析
16. 如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“ $\to$ ”方向排列，如（1，0），（2，0），（2，1），（3，2），（3，1），（3，0）……根据这个规律探究可得，第22个点的坐标为．

查看试题解析

三、解答题

17. 计算： $9 \div (- \frac{3}{2}) + \sqrt{16} - 6 \times \sqrt[3]{\frac{1}{27}}$ ．

查看试题解析
18. 解方程组．

(1)、 ${\begin{array}{l} x - y = 3 \\ 2 x + y = 0 \end{array}$

(2)、解方程组 ${\begin{array}{l} 3 (x + y) - 4 (x - y) = 4 \\ \frac{x + y}{2} + \frac{x - y}{6} = 1 \end{array}$ ；

查看试题解析
19. 已知2的平方等于 $a$ ， $(2 b - 1)$ 是27的立方根，士 $\sqrt{c - 2}$ 表示3的平方根，求 $2 a - b + c$ 的值.

查看试题解析
20. 如图，已知AB $∥$ CD，∠B=∠D，BE与DF平行吗？请完成下面证明过程．
解：BE与DF平行．
理由：∵AB $∥$ CD（已知），
∴∠B=∠COE（   ），
又∵∠B=∠D（   ），
∴∠D=∠COE（    ），
∴BE $∥$ DF（    ）．

查看试题解析
21. 某校在一次大课间活动中，采用了四种活动形式：A：跑步；B：跳绳；C：做操；D：游戏，全校学生都选择了一种形式参与活动，小明对同学们选择的活动形式进行了随机抽样调查，并绘制了不完整的两幅统计图，结合统计图，回答下列问题：

(1)、本次调查学生共人，并将条形图补充完整；

(2)、如果该校有学生2000人，请你估计该校选择“跑步”这种活动的学生约有多少人？

查看试题解析
22. 在平面直角坐标系xOy中，点A的坐标为（0，4），线段MN的位置如图所示，其中点M的坐标为（﹣3，﹣1），点N的坐标为（3，﹣2）．

(1)、将线段MN平移得到线段AB，其中点M的对应点为A，点N的对称点为B．
①点M平移到点A的过程可以是：先向平移个单位长度，再向平移个单位长度；

②点B的坐标为；

(2)、在（1）的条件下，若点C的坐标为（4，0），连接AC，BC，求△ABC的面积．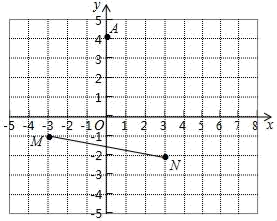

查看试题解析
23. 某班在疫情期间利用网络组织一次防新冠病毒知识竞赛，为奖励表现优秀的同学，班主任拿出131元钱作为购买奖品费用，初步确定购买水杯或笔袋作为奖品，她在文具店了解到一个水杯的价格为 25元，一个笔袋的价格为8元.

(1)、若班主任单购买水杯，最多能买多少个？

(2)、若班主任购买水杯和笔袋共10个（水杯和笔袋都要购买），有哪几种购买方案？

查看试题解析
24. 如图，在平面直角坐标系中，点O为坐标原点，三角形OAB的边OA、OB分别在x轴正半轴上和y轴正半轴上，A（a，0），a是方程 $\frac{a + 2}{3} - \frac{a - 2}{2} = 1$ 的解，且△OAB的面积为6．

(1)、求点A、B的坐标；

(2)、将线段OA沿轴向上平移后得到PQ，点O、A的对应点分别为点P和点Q（点P与点B不重合），设点P的纵坐标为t，△BPQ的面积为S，请用含t的式子表示S；

(3)、在（2）的条件下，设PQ交线段AB于点K，若PK= $\frac{8}{3}$ ，求t的值及△BPQ的面积．

查看试题解析