河南省商丘市名校2021-2022学年高一下学期数学期末考试试卷

试卷更新日期：2022-08-02 类型：期末考试

进入出卷网下载

一、单选题

1. 已知复数z满足 $z = (1 - \sqrt{3} i) (2 + \sqrt{3} i)$ ，则 $| z | =$ （）

A、 $2 \sqrt{7}$ B、5 C、 $2 \sqrt{5}$ D、 $3 \sqrt{2}$

查看试题解析
2. 某射击运动员6次的训练成绩分别为：80，82，89，90，91，86，则这6次成绩的第80百分位数为（）

A、89 B、89.5 C、90 D、91

查看试题解析
3. 已知i是虚数单位，若 $\frac{2 + i}{1 - i} = a - b i (a ， b \in R)$ ，则 $2 a + b$ 的值是（）

A、-2 B、 $- \frac{1}{2}$ C、 $\frac{5}{2}$ D、1

查看试题解析
4. 已知向量 $\vec{a} = (λ ， 9)$ ， $\vec{b} = (1 ， λ)$ 共线且方向相同，则 $λ$ 的值等于（）

A、3 B、-3 C、±3 D、 $\frac{1}{3}$

查看试题解析
5. 现利用随机数法从高一（3）班的50名同学中选取5名同学参与学校活动.该班同学分别编号为01，02，…，49，50.选取方法是从随机数表第1行第6列的数开始由左到右依次选取两个数字，则选出来的第5个个体的编号为（）
（注：下表为随机数表的第1行和第2行）
7816
6572
0802
6314
0702
4369
9728
0198
3204
9243
4935
8200
3623
4869
6938
7481

A、31 B、40 C、36 D、24

查看试题解析
6. m，n是空间中不同的直线， $α$ ， $β$ 是不同的平面，则下列说法不正确的是（）

A、若 $m ∥ β$ 且 $m ⊥ α$ ，则 $α ⊥ β$ B、若 $m ⊥ α$ ， $n ⊥ β$ ， $α ⊥ β$ ，则直线m与n相交或异面 C、若 $m ⊥ α$ ， $n ∥ β$ ， $α ⊥ β$ ，则直线m与n一定垂直 D、若 $m \subset α$ ， $n \subset β$ ， $α ∥ β$ ，则m与n异面或平行

查看试题解析
7. 在△ABC中，已知 $s i n B = 2 s i n (B + C) c o s C$ ，那么△ABC一定是（）

A、等腰直角三角形 B、等腰三角形 C、直角三角形 D、等边三角形

查看试题解析
8. 下列关于棱锥､棱台的说法正确的是（）

A、有两个面平行且相似，其他各面都是梯形的多面体是棱台 B、用一个平面去截棱锥，底面与截面之间部分所围成的几何体叫做棱台 C、棱台的侧面展开图是由若干个等腰梯形组成的 D、棱台的各侧棱延长后必交于一点

查看试题解析
9. 为了贯彻落实中央新疆工作座谈会和全国对口支援新疆工作会议精神，促进新疆教育事业发展，甲､乙､丙三个城市选取300名教师支援新疆的教育事业.已知乙城市教师人数有18600人，丙城市教师人数有41400人，如果用比例分配的分层随机抽样的办法，甲城市需要选派100人，那么甲城市总共有教师人数为（）

A、10000 B、20000 C、24000 D、30000

查看试题解析
10. 已知袋子中有10个小球，其中红球2个，黑球和白球共8个，从中随机取出一个，设取出红球为事件A，取出黑球为事件B，随机事件C与B对立.若 $P (A + B) = 0.5$ ，则 $P (C) =$ （）

A、0.3 B、0.6 C、0.7 D、0.8

查看试题解析
11. 在如图（1）所示的四棱锥 $A - B C D E$ 中，底面 $B C D E$ 为正方形，且侧面 $A B C$ 垂直于底面 $B C D E$ ，水平放置的侧面 $A B C$ 的斜二测直观图如图（2）所示，已知 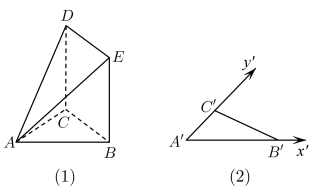$A^{'} B^{'} = 2$ ， $A^{'} C^{'} = 1$ ，则四棱锥 $A - B C D E$ 的侧面积是（）

A、 $12 + \sqrt{34}$ B、 $20 + 2 \sqrt{34}$ C、 $2 + 2 \sqrt{2} + 2 \sqrt{5}$ D、 $2 + 4 \sqrt{2} + 2 \sqrt{5}$

查看试题解析
12. 已知D为△ABC所在平面内一点，AD交BC于点E，且 $6 \vec{A D} = 2 \vec{A B} + 3 \vec{A C}$ ，则 $\frac{{S_{△}}_{E C D}}{{S_{△}}_{A B D}} =$ （）

A、 $\frac{1}{5}$ B、 $\frac{1}{2}$ C、 $\frac{2}{15}$ D、 $\frac{3}{10}$

查看试题解析

二、填空题

13. 复数 $z = c o s \frac{2021 π}{3} - i s i n \frac{2023 π}{3}$ 在复平面内对应的点位于第象限.

查看试题解析
14. 制造业直接体现了一个国家的生产力水平，中国制造业作为国家的支柱产业，一直保持较好的发展态势.通过人口普查发现，A，B两市从事制造业的人分别占全市人口的8%，12%，这两市的人口数之比为 $6 ： 9$ .现从这两市随机选取一个人，则此人恰好从事制造业的概率为.

查看试题解析
15. 在四棱锥 $P - A B C D$ 中， $P A ⊥$ 平面 $A B C D$ ，底面 $A B C D$ 为矩形， $P A = A D = 2$ ， $A B = 2 \sqrt{2}$ ，则四棱锥 $P - A B C D$ 的外接球的体积为.

查看试题解析
16. 地面上一名观测工作人员，观测到一架飞机以 $300 \sqrt{3}$ $k m / h$ 的速度在某一高度向正东方向飞行，在观测点上第一次观测到飞机在北偏西 $\frac{π}{3}$ 方向，1分钟后第二次观测到飞机在北偏东 $\frac{5 π}{12}$ 方向，仰角为 $\frac{π}{3}$ ，则飞机的飞行高度为 $k m$ （结果保留根号）.

查看试题解析

三、解答题

17. 已知平面内三个向量 $\vec{a} = (2 ， 3)$ ， $\vec{b} = (- 1 ， 3)$ ， $\vec{c} = (1 ， 4)$ .

(1)、求满足 $2 \vec{a} = m \vec{b} + n \vec{c}$ 的实数m，n；

(2)、当k为何值时， $k \vec{a} + \vec{b}$ 与 $\vec{a} + 2 \vec{c}$ 垂直？

查看试题解析
18. 某中学为调研学生在餐厅用餐的满意度，在本校学生中随机抽取了100人，对餐厅进行评分，满分为100分.整理评分数据，将分数以20为组距分为4组，依次为：[20，40），[40，60），[60，80），[80，100]，得到频率分布直方图如图所示（同一组中的数据以该组区间的中点值为代表）.

(1)、估计该校餐厅得分的80%分位数､众数､中位数；

(2)、估计该校餐厅得分的平均数 $\bar{x}$ 和方差 $s^{2}$ .

查看试题解析
19. 如图，在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A B = A A_{1} = 2$ ， $B C = 3$ ， E，F分别为 $C D_{1}$ ， $A B$ 的中点.

(1)、求证： $E F ∥$ 平面 $B B_{1} C_{1} C$ ；

(2)、求二面角 $F - C D_{1} - D$ 的余弦值.

查看试题解析
20. 甲､乙､丙三名篮球运动员进行投篮比赛，甲投篮命中的概率为 $\frac{1}{2}$ ，乙投篮命中的概率为 $\frac{1}{3}$ ，丙投篮命中的概率为 $\frac{1}{4}$ ，每人只投篮一次.

(1)、求三人都投篮命中的概率；

(2)、求三人中有人投篮命中的概率；

(3)、求三人中恰有两人投篮命中的概率.

查看试题解析
21. 记△ABC的内角A，B，C的对边分别为a，b，c， $a^{2} + c^{2} - b^{2} = 4$ ， $s i n B = \frac{\sqrt{15}}{4}$ .

(1)、求△ABC的面积；

(2)、若 $s i n A s i n C = \frac{1}{2}$ ，求△ABC的周长.

查看试题解析
22. 在四棱锥P-ABCD中， $P A ⊥$ 平面ABCD，E为PD的中点，F为PC的中点，PA=AD=2，AB=BC=1， $∠ B A D = ∠ A B C = \frac{π}{2}$ .

(1)、求证：平面 $P A C ⊥$ 平面AEF；

(2)、求直线PA与平面AEF所成角的正弦值.

查看试题解析

7816	6572	0802	6314	0702	4369	9728	0198
3204	9243	4935	8200	3623	4869	6938	7481