广东省湛江市2021-2022学年高一下学期数学期末考试试卷
试卷更新日期:2022-08-01 类型:期末考试
一、单选题
-
1. 某学校有高中学生2000人,其中高一年级、高二年级、高三年级的人数分别为700,660,640.为调查学生参加“社区志愿服务”的意向,现采用分层抽样的方法从中抽取一个容量为100的样本,那么应抽取高二年级学生的人数为( )A、32 B、33 C、64 D、662. 已知集合 , , 则集合( )A、 B、 C、 D、3. 若直线l与平面α相交,则( )A、平面α内存在直线与l异面 B、平面α内存在唯一一条直线与l平行 C、平面α内存在唯一一条直线与l垂直 D、平面α内的直线与l都相交4. 复数(是虚数单位),则在复平面内对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 在中,已知 , 则( )A、3 B、2 C、 D、6. 在 中,内角 所对的边分别是 ,“ ”是“ ”的( )A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分又不必要条件7. 设 , , , , 则这四个数的大小关系是( )A、 B、 C、 D、8. 如图,角的始边与轴的非负半轴重合,终边与单位圆交于点 , 角的始边与角的始边重合,且终边与单位圆交于点 , 记.若角为锐角,则的取值范围是( )
 A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
9. 下列函数为偶函数且在上是增函数的是( )A、 B、 C、 D、10. 下列各式中,值为的是( )A、 B、 C、 D、11. 已知向量 , , , 则下列结论正确的有( )A、 B、若 , 则 C、的最大值为2 D、的最小值为12. 如图,正方体的棱长为1,线段上有两个动点 , , 且 , 则下列结论中正确的是( )
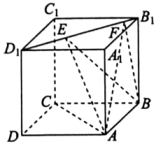 A、 B、平面 C、三棱锥的体积为定值 D、的面积与的面积相等
A、 B、平面 C、三棱锥的体积为定值 D、的面积与的面积相等三、填空题
-
13. 若 , 则.14. 从3名男同学和2名女同学中任选2名同学参加志愿者服务,则选出的2名同学中至少有1名女同学的概率是.15. 已知 , , 是单位圆上的三点,且 , 则.16. 对实数、定义一个运算: , 设函数(),若函数的图象与轴恰有两个公共点,则实数的取值范围是 .
四、解答题
-
17. 已知向量 , , , .(1)、若与共线,求实数;(2)、求的最小值及相应的值.18. 已知.(1)、化简并求函数图象的对称轴方程;(2)、当时,求函数的最大值和最小值.19. 移动支付为人民群众的生活带来极大的方便.为了解某地区居民移动支付的使用情况,随机调查了该地区100名居民在一星期内使用移动支付的相关情况,列表如下:
支付次数
人数
30
25
10
已知这100名居民中一星期内使用移动支付次数超过30次的占55%.
(1)、求 , 的值;(2)、估计该地区居民在一星期内使用移动支付次数超过45次的概率.
