广东省汕尾市2021-2022学年高一下学期数学期末考试试卷

试卷更新日期：2022-08-01 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | x \geq - \frac{3}{5}}$ ， $B = {x \in Z | x^{2} \leq 1}$ ，则 $A \cap B =$ （）

A、 ${1}$ B、 ${0 ， 1}$ C、 ${- 1 ， 0 ， 1}$ D、 $[- \frac{3}{5} ， 1]$

查看试题解析
2. 已知实数 $a$ ， $b$ 满足 $a < b$ ，则下列关系式一定成立的是（）

A、 $a^{2} < b^{2}$ B、 $l n (b - a) > 0$ C、 $\frac{1}{a} > \frac{1}{b}$ D、 $2^{a} < 2^{b}$

查看试题解析
3. 已知 $| \vec{a} | = | \vec{b} | = 1$ ，向量 $\vec{a}$ 与 $\vec{b}$ 的夹角为 $60 °$ ，则 $| 3 \vec{a} - 4 \vec{b} | =$ （）

A、5 B、 $\sqrt{19}$ C、 $3 \sqrt{2}$ D、 $\sqrt{13}$

查看试题解析
4. 若棱长为 $2 \sqrt{2}$ 的正方体的顶点都在同一球面上，则该球的表面积为（）．

A、12π B、24π C、36π D、144π

查看试题解析
5. 在 $△ A B C$ 中，已知 $A C = 1 ， B C = \sqrt{3} ， B = \frac{π}{6}$ ，则角 $C$ 为（）

A、 $\frac{π}{2}$ B、 $\frac{π}{4}$ C、 $\frac{π}{2}$ 或 $\frac{π}{6}$ D、 $\frac{π}{6}$ 或 $\frac{5 π}{6}$

查看试题解析
6. 已知 $c o s (α - \frac{π}{6}) + s i n α = \frac{4 \sqrt{3}}{5}$ ，则 $c o s (\frac{2 π}{3} + α)$ 的值是（）

A、 $- \frac{4}{5}$ B、 $\frac{4}{5}$ C、 $- \frac{2 \sqrt{3}}{5}$ D、 $\frac{2 \sqrt{3}}{5}$

查看试题解析
7. 如图，已知 $\vec{A B} = 2 \vec{B P}$ ，则 $\vec{O P} =$ （）

A、 $\frac{1}{2} \vec{O A} - \frac{3}{2} \vec{O B}$ B、 $- \frac{1}{2} \vec{O A} + \frac{3}{2} \vec{O B}$ C、 $\frac{1}{2} \vec{O A} + \frac{3}{2} \vec{O B}$ D、 $- \frac{1}{2} \vec{O A} - \frac{3}{2} \vec{O B}$

查看试题解析
8. 一纸片上绘有函数 $f (x) = \sqrt{2} s i n (ω x - \frac{π}{4})$ （ $ω > 0$ ）一个周期的图像，现将该纸片沿x轴折成直二面角，原图像上相邻的最高点和最低点此时的空间距离为 $2 \sqrt{2}$ ，若方程 $f (x) = - 1$ 在区间 $(0 ， a)$ 上有两个实根，则实数a的取值范围是（）

A、 $(4 ， 7)$ B、 $(4 ， 7]$ C、 $[4 ， 7)$ D、 $[4 ， 7]$

查看试题解析

二、多选题

9. 下面是关于复数 $z = \frac{2}{- 1 + i}$ 的四个命题，其中真命题为（）

A、 $z^{2} = 2 i$ B、 $| z | = 2$ C、 $z$ 的虚部为-1 D、 $z$ 的共轭复数为 $1 + i$

查看试题解析
10. 已知m，n是两条不同的直线， $α$ ， $β$ 是两个不同的平面，则下列说法正确的是（）

A、若 $α / / β$ ， $m \subset α$ ， $n \subset β$ ，则 $m / / n$ B、若 $m ⊥ α$ ， $m / / n$ ， $n ⊥ β$ ，则 $α / / β$ C、若 $α ⊥ β$ ， $m \subset α$ ， $n \subset β$ ，则 $m ⊥ n$ D、若 $m ⊥ α$ ， $m / / n$ ， $n / / β$ ，则 $α ⊥ β$

查看试题解析
11. 正四棱台 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，上底面 A₁B₁C₁D₁ 的边长为2，下底面 $A B C D$ 的边长为4，棱台高为1，则（）

A、该四棱台的侧棱长为 $\sqrt{3}$ B、 $A A_{1}$ 与 $B C$ 所成角的余弦值为 $\frac{1}{3}$ C、 $A A_{1}$ 与面 $A B C D$ 所成的角大小为 $\frac{π}{4}$ D、二面角 $A - B C - B_{1}$ 的大小为 $\frac{π}{4}$

查看试题解析
12. 在 $△ A B C$ 中，A，B，C的对边分别为a，b，c，R为 $△ A B C$ 外接圆的半径， $△ A B C$ 的面积记为 $S_{△ A B C}$ ，则下列命题正确的是（）

A、 $s i n A < s i n B$ 的充要条件是 $A < B$ B、若 $a c o s B - b c o s A = c$ ，则 $△ A B C$ 是直角三角形 C、若 $b = 3$ ， $A = 60 °$ ， $S_{△ A B C} = 3 \sqrt{3}$ ，则 $R = \frac{\sqrt{13}}{3}$ D、不存在 $△ A B C$ ，满足 $a = 5$ ， $b = 10$ ， $A = \frac{π}{4}$ 同时成立

查看试题解析

三、填空题

13. 已知向量 $\vec{a} = (2 ， 3)$ ， $\vec{b} = (λ ， 4)$ ，若 $\vec{a} / / \vec{b}$ ，则 $λ =$ .

查看试题解析
14. 已知函数 $f (x) = {\begin{array}{l} l g x ， x > 0 \\ 2^{x} ， x < 0 \end{array}$ ，则 $f (f (\frac{1}{10})) =$ .

查看试题解析
15. 已知函数 $f (x) = c o s (4 x + φ)$ （ $φ \in R$ ），将 $y = f (x)$ 图象上所有点向右平移 $\frac{π}{6}$ 个单位，得到奇函数 $y = g (x)$ 的图象，则常数 $φ$ 的一个取值为.

查看试题解析
16. 在平面四边形 $A B C D$ 中， $A B ⊥ A D$ ， $A B = 6$ ， $A D = 8$ ， $A C = 18$ ， $A C$ 交 $B D$ 于点O，若 $\vec{C A} = m \vec{C B}$ $+ (\frac{3}{2} - m) \vec{C D}$ ，则 $\frac{A O}{O C}$ 的值为， $O D$ 的长为.

查看试题解析

四、解答题

17. 在平而直角坐标系 $x O y$ 中，设与x轴、y轴方向相同的两个单位向量分别为 $\vec{i}$ 和 $\vec{j}$ ， $\vec{O A} = \vec{i} + 2 \vec{j}$ ， $\vec{O B} = 2 \vec{i} - 4 \vec{j}$ .

(1)、求向量 $\vec{O A}$ 与 $\vec{O B}$ 夹角的余弦值；

(2)、若点P是线段 $A B$ 的中点，且向量 $\vec{O P}$ 与 $\vec{O A} + k \vec{O B}$ 垂直，求实数k的值.

查看试题解析
18. 已知函数 $f (x) = \sqrt{3} s i n ω x c o s ω x - c o s^{2} ω x + \frac{1}{2}$ ，其中 $ω > 0$ ， $x_{1}$ ， $x_{2}$ 是函数 $f (x)$ 的两个零点，且 $| x_{1} - x_{2} |$ 的最小值为 $\frac{π}{2}$ .

(1)、求使 $f (x)$ 取得最大值时自变量x的集合，并求 $f (x)$ 的最大值；

(2)、求 $f (x)$ 的单调递增区间.

查看试题解析
19. 如图， $A B$ 是圆 $O$ 的直径，点 $C$ 是圆 $O$ 上异于 $A$ ， $B$ 的点，直线 $P C ⊥$ 平面 $A B C$ ， $E$ ， $F$ 分别是线段 $P A$ ， $P C$ 的中点．

(1)、证明：平面 $B E F ⊥$ 平面 $P B C$ ；

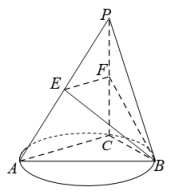(2)、记平面 $B E F$ 与平面 $A B C$ 的交线为 $l$ ，试判断直线 $E F$ 与直线 $l$ 的位置关系，并说明理由．

查看试题解析
20. 设a，b，c分别为 $△ A B C$ 三个内角A，B，C的对边，已知 $b s i n A = a c o s (B - \frac{π}{6})$ .

(1)、求角B；

(2)、若 $b = 6$ ，且 $s i n B + s i n (C - A) = 2 s i n 2 A$ ，求边c.

查看试题解析
21. 在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，D，E分别是 $A A_{1}$ ， $B_{1} C_{1}$ 的中点， $A A_{1} = 2$ ， $A C = B C = 1$ ， $A B = \sqrt{2}$ ， $D C_{1} ⊥ B D$ .

(1)、求证： $A_{1} E / /$ 平面 $C_{1} B D$ ；

(2)、求点 $A_{1}$ 到平面 $C_{1} B D$ 的距离.

查看试题解析
22. 某大学科研团队在如下图所示的长方形区域 $A B C D$ 内（包含边界）进行粒子撞击实验，科研人员在A、O两处同时释放甲、乙两颗粒子.甲粒子在A处按 $\vec{A M}$ 方向做匀速直线运动，乙粒子在O处按 $\vec{O N}$ 方向做匀速直线运动，两颗粒子碰撞之处记为点P，且粒子相互碰撞或触碰边界后爆炸消失.已知 $A B$ 长度为6分米，O为 $A B$ 中点.

(1)、已知向量 $\vec{A M}$ 与 $\vec{O N}$ 的夹角为 $\frac{π}{3}$ ，且 $A D$ 足够长.若两颗粒子成功发生碰撞，求两颗粒子运动路程之和的最大值；

(2)、设向量 $\vec{A M}$ 与向量 $\vec{A O}$ 的夹角为 $α$ （ $0 < α < π$ ），向量 $\vec{O N}$ 与向量 $\vec{O B}$ 的夹角为 $β$ （ $0 < β < π$ ），甲粒子的运动速度是乙粒子运动速度的2倍.请问 $A D$ 的长度至少为多少分米，才能确保对任意的 $β \in (0 ， π)$ ，总可以通过调整甲粒子的释放角度 $α$ ，使两颗粒子能成功发生碰撞？

查看试题解析