广东省七区2021-2022学年高一下学期数学期末联考试卷

试卷更新日期：2022-08-01 类型：期末考试

进入出卷网下载

一、单选题

1. 集合 $A = {x | - 1 \leq x < 2} ， B = {x | x > 1}$ ，则 $A ∩ (∁_{R} B) =$ （）

A、 ${x | - 1 \leq x < 1}$ B、 ${x | - 1 \leq x \leq 1}$ C、 ${x | 1 \leq x < 2}$ D、 ${x | x < 2}$

查看试题解析
2. 复数 $z = \frac{2}{i + 1}$ （ $i$ 为虚数单位）的虚部是（）

A、-1 B、1 C、 $- i$ D、2

查看试题解析
3. 下列函数既是偶函数又在 $(0 ， + ∞)$ 上单调递减的是（）

A、 $y = x^{- 2}$ B、 $y = x^{3}$ C、 $y = | x |$ D、 $y = \sqrt{x}$

查看试题解析
4. 如图正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为a，以下结论中，错误的是（）

A、异面直线 $A_{1} D$ 与 $A B_{1}$ 所成的角为 $60 °$ B、直线 $A_{1} D$ 与 $B C_{1}$ 垂直 C、直线 $A_{1} D$ 与 $B D_{1}$ 平行 D、直线 $A_{1} D$ 与 $B_{1} C$ 平行

查看试题解析
5. 高一某班10名学生的英语口语测试成绩（单位：分）如下：76，90，84，82，81，87，86，82，85，83.这组数据的第75百分位数是（）

A、85 B、86 C、85.5 D、86.5

查看试题解析
6. 函数 $y = (3^{x} - 3^{- x}) c o s x$ 在区间 $[- \frac{π}{2} ， \frac{π}{2}]$ 的图象大致为（）

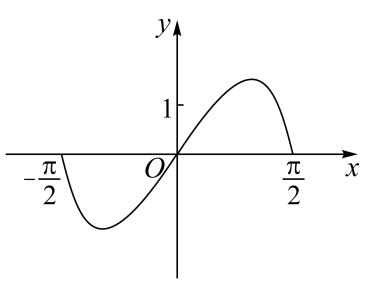A、 B、 C、 D、

查看试题解析
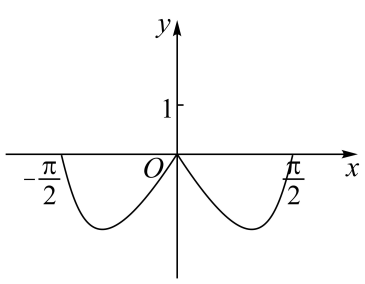7. 国庆节放假，甲回老家过节的概率为 $\frac{1}{3}$ ，乙、丙回老家过节的概率分别为 $\frac{1}{4}$ ， $\frac{1}{5}$ .假定三人的行动相互之间没有影响，那么这段时间内至少1人回老家过节的概率为（）

A、 $\frac{59}{60}$ B、 $\frac{3}{5}$ C、 $\frac{1}{2}$ D、 $\frac{1}{60}$

查看试题解析
8. 已知正三棱锥 $P - A B C$ 的四个顶点都在半径为R的球面上，且 $A B = 2$ ，若三棱锥 $P - A B C$ 的体积为 $\frac{\sqrt{3}}{2} R$ ，则该球的表面积为（）

A、 $\frac{32 π}{27}$ B、 $\frac{16 π}{9}$ C、 $\frac{64 π}{27}$ D、 $\frac{64 π}{9}$

查看试题解析

二、多选题

9. 设a，b是空间中不同的直线， $α ， β ， γ$ 是不同的平面，则下列说法正确的是（）

A、若 $a ∥ b ， b \subset α ， a ⊄ α$ ，则 $a ∥ α$ B、若 $a \subset α ， b \subset β ， α ∥ β$ ，则 $a ∥ b$ C、若 $a \subset α ， b \subset α ， a ∥ β ， b ∥ β$ ，则 $α ∥ β$ D、若 $α ∥ β ， α ∩ γ = a ， β ∩ γ = b$ ，则 $a ∥ b$

查看试题解析
10. 已知 $\overset{⇀}{a} = (1 ， 2) ， \overset{⇀}{b} = (m ，－ 1)$ ，则下列结论正确的是（）

A、若 $\vec{a} ∥ \vec{b}$ ，则 $m = \frac{1}{2}$ B、若 $\vec{a} ⊥ \vec{b}$ ，则 $m = 2$ C、若 $| \vec{a} | = | \vec{b} |$ ，则 $m = 2$ D、若 $m = - 3$ ，则 $\vec{a} ， \vec{b}$ 的夹角为 $\frac{3 π}{4}$

查看试题解析
11. 已知函数 $f (x) = 2 s i n (4 x + \frac{π}{6})$ ，则（）

A、f(x)的最小正周期为 $\frac{π}{2}$ B、f(x)的图象关于直线 $x = \frac{π}{6}$ 对称 C、f(x)在区间 $[\frac{π}{12} ， \frac{π}{3}]$ 上单调递减 D、f(x)的图象关于点 $(- \frac{π}{24} ， 0)$ 对称

查看试题解析
12. 给出下列结论，其中正确的结论是（）

A、函数 $y = {(\frac{1}{2})}^{- x^{2} + 1}$ 的最大值为 $\frac{1}{2}$ B、若定义在R上的奇函数 $f (x)$ 在 $(- \infty ， 0)$ 内有100个零点，则函数 $f (x)$ 有201个零点 C、在同一平面直角坐标系中，函数 $y = 2^{x}$ 与 $y = l o g_{2} x$ 的图象关于直线 $y = x$ 对称 D、已知函数 $y = l o g_{a} (2 - a x)$ （ $a > 0$ 且 $a \neq 1$ ）在 $(0 ， 1)$ 上是减函数，则实数a的取值范围是 $(1 ， 2)$

查看试题解析

三、填空题

13. 函数 $f (x) = \sqrt{3} s i n x + c o s x$ 的最小值为．

查看试题解析
14. 为加速推进科技城新区建设，需了解某科技公司的科研实力，现拟采用分层抽样的方式从A，B，C三个部门中抽取16名员工进行科研能力访谈 $.$ 已知这三个部门共有64人，其中B部门24人，C部门32人，则从A部门中抽取的访谈人数．

查看试题解析
15. 已知向量 $\vec{a}$ ， $\vec{b}$ 满足 $| \vec{a} | = 2$ ， $| \vec{b} | = 1$ ， $\vec{a}$ 与 $\vec{b}$ 的夹角为 $\frac{2 π}{3}$ ，则 $\vec{a}$ 在 $\vec{b}$ 上的投影向量为.

查看试题解析
16. 正多面体被古希腊圣哲认为是构成宇宙的基本元素，加上它们的多种变体，一直是科学、艺术、哲学灵感的源泉之一.如图，该几何体是一个棱长为2的正八面体，则此正八面体的体积与表面积之比为.

查看试题解析

四、解答题

17. 已知 $a ， b ， c$ 分别为 $△ A B C$ 内角 $A ， B ， C$ 的对边，且 $\frac{s i n B}{c o s A} = \frac{\sqrt{3} b}{a}$ ．

(1)、求角A；

(2)、若 $a = \sqrt{7} ， b = 2$ ，求c．

查看试题解析
18. 某餐厅销售一款饮料，定价为4元/瓶，20天的日销量数据按照 $[15 ， 25] ， (25 ， 35] ， (35 ， 45] ， (45 ， 55]$ ，分组，得到如下频率分布直方图．

(1)、估计该餐厅这款饮料的平均日销售额（销量 $\times$ 定价）；

(2)、若从这款饮料销量大于35瓶的数据中任取两天的数据，求这两天的饮料销量都大于45瓶的概率．

查看试题解析
19. 如图，已知三棱锥 $P - A B C$ ， $P A ⊥$ 平面 $A B C$ ， $∠ A C B = 9 0^{∘}$ ， $∠ B A C = 6 0^{∘}$ ， $P A = A C = 2$ ， M、N分别是PB、AB的中点．

(1)、求证： $M N$ //平面 $P A C$ ；

(2)、求直线 $C M$ 与平面 $A B C$ 所成角的正弦值．

查看试题解析
20. 如图，在平行四边形ABCD中，点E是AB的中点，点F，G分别是AD，BC的三等分点 $(A F = \frac{1}{3} A D ， B G = \frac{1}{3} B C)$ .设 $\vec{A B} = \vec{a} ， \vec{A D} = \vec{b}$ .

(1)、用 $\vec{a} ， \vec{b}$ 表示 $\vec{E F} ， \vec{E G}$ ；

(2)、如果 $| \vec{b} | = \frac{3}{2} | \vec{a} |$ ， EF，EG有什么位置关系？用向量方法证明你的结论.

查看试题解析
21. 如图，在三棱锥S—ABC中，SC⊥平面ABC，点P、M分别是SC和SB的中点，设PM=AC=1，∠ACB=90°，直线AM与直线SC所成的角为60°.

(1)、求证：平面MAP⊥平面SAC.

(2)、求二面角M—AC—B的平面角的正切值；

查看试题解析
22. 设函数 $f (x) = a x^{2} - (a + 1) x + 1$ ．

(1)、当 $a \in R^{+}$ 时，求关于x的不等式 $f (x) < 0$ 的解集．

(2)、若 $g (x) = x^{3} - x^{2} + 1$ ，当 $x \in [\frac{4}{3} ， + \infty)$ 时，不等式 $f (x) \leq g (x)$ 恒成立，求实数a的取值范围．

查看试题解析