广东省茂名市电白区2021-2022学年高一下学期数学期末试试卷

试卷更新日期：2022-08-01 类型：期末考试

进入出卷网下载

一、单选题

1. 已知复数：满足 $z = \frac{5}{2 + i}$ （ $i$ 为虚数单位），则 $\bar{z} =$ （）

A、 $2 + i$ B、 $2 - i$ C、 $1 + 2 i$ D、 $1 - 2 i$

查看试题解析
2. 下列问题中最适合用简单随机抽样方法的是（）

A、某学校有学生1 320人，卫生部门为了了解学生身体发育情况，准备从中抽取一个容量为300的样本 B、为了准备省政协会议，某政协委员计划从1 135个村庄中抽取50个进行收入调查 C、从全班30名学生中，任意选取5名进行家访 D、为了解某地区癌症的发病情况，从该地区的5 000人中抽取200人进行统计

查看试题解析
3. 2021年是中国共产党成立100周年，为了庆祝建党100周年，激发青少年学生的爱国、爱党热情，引导青少年学生深入地了解党的光辉历史，加强爱国主义教育，甲、乙两所学校均计划于2021年7月组织师生参加“观看一部红色电影”活动．据了解，《1921》、《革命者》、《红船》、《三湾改编》等多部电影将陆续上映．甲、乙两校分别从这4部电影中任选一部电影观看，则甲、乙两校选择不同电影观看的概率是（）

A、 $\frac{4}{9}$ B、 $\frac{5}{9}$ C、 $\frac{1}{4}$ D、 $\frac{3}{4}$

查看试题解析
4. 如图，在 $Δ A B C$ 中， $\overset{⇀}{A N} = \frac{1}{2} \overset{⇀}{A C} ， P$ 是 $B N$ 的中点，若 $\overset{⇀}{A P} = m \overset{⇀}{A B} + \frac{1}{4} \overset{⇀}{A C}$ ，则实数 $m$ 的值是（）

A、 $\frac{1}{4}$ B、1 C、 $\frac{1}{2}$ D、 $\frac{3}{2}$

查看试题解析
5. 光明学校为了解男生身体发育情况，从2000名男生中抽查了100名男生的体重情况，根据数据绘制样本的频率分布直方图，如图所示，下列说法中错误的是（）

A、样本的众数约为 $67 \frac{1}{2}$ B、样本的中位数约为 $66 \frac{2}{3}$ C、样本的平均值约为66 D、体重超过75kg的学生频数约为200人

查看试题解析
6. 有5个相同的球，分别标有数字1，2，3，4，5，从中有放回的随机取两次，每次取1个球，甲表示事件“第一次取出的球的数字是1”，乙表示事件“第二次取出的球的数字是2”，丙表示事件“两次取出的球的数字之和是7”，丁表示事件“两次取出的球的数字之和是6”，则（）

A、甲与丙相互独立 B、丙与丁相互独立 C、甲与丁相互独立 D、乙与丙相互独立

查看试题解析
7. 如图，在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A B = 2$ ， $M$ ， $N$ 分别为 $A_{1} D_{1}$ ， $B_{1} C_{1}$ 的中点， $E$ ， $F$ 分别为棱 $A B$ ， $C D$ 上的动点，则三棱锥 $M - N E F$ 的体积（）

A、存在最大值，最大值为 $\frac{8}{3}$ B、存在最小值，最小值为 $\frac{2}{3}$ C、为定值 $\frac{4}{3}$ D、不确定，与 $E$ ， $F$ 的位置有关

查看试题解析
8. 将函数 $f (x) = 2 s i n x - 1$ 的图象上所有点的纵坐标伸长为原来的2倍，再向下平移1个单位长度，最后向左平移 $φ (φ > 0)$ 个单位长度，得到函数 $g (x)$ 的图象.若对任意 $x_{1} \in [0 ， \frac{π}{2}]$ ，都存在 $x_{2} \in [- \frac{π}{2} ， 0]$ ，使得 $f (x_{1}) = g (x_{2})$ ，则 $φ$ 的值可能是（）

A、 $\frac{π}{4}$ B、 $\frac{5 π}{12}$ C、 $\frac{7 π}{12}$ D、 $\frac{3 π}{4}$

查看试题解析

二、多选题

9. 一种新冠病毒变种在多个国家和地区蔓延扩散，令全球再度人心惶惶．据悉，新冠病毒变种被世界卫生组织定义为“关切变异株”，被命名为奥密克戎（Omicron）．根据初步研究发现，奥密克戎变异株比贝塔（Beta）变异株和德尔塔（Delta）变异株具有更多突变，下图是某地区奥密克戎等病毒致病比例（新增病例占比）随时间变化的对比图，则下列说法正确的有（）

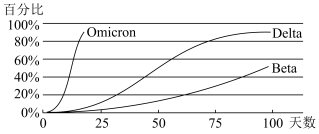A、奥密克戎变异株感染的病例不到25天占据新增病例的80%多 B、德尔塔变异株用了100天占据该地区约50%的新增病例 C、贝塔变异株的传染性比德尔塔变异株的传染性强 D、德尔塔变异株感染的病例占新增病例80%用了约75天

查看试题解析
10. 从2名男同学和3名女同学中任选2人参加社区服务，记事件“选中的2人都是女同学”的概率为 $P_{1}$ ；事件“选中2人都是男同学”的概率为 $P_{2}$ ；事件“选中1名男同学1名女同学”的概率 $P_{3}$ ．则下列选项正确的是（）

A、 $P_{1} + P_{2} = P_{3}$ B、 $2 P_{1} = P_{3}$ C、 $P_{1} > 2 P_{2}$ D、 ${P_{1}}^{2} = P_{2} P_{3}$

查看试题解析
11. 《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”；底面为矩形，一条侧棱垂直于底面的四棱锥称之为“阳马”；四个面均为直角三角形的四面体称为“鳖膈”．如图在堑堵 $A B C - A_{1} B_{1} C_{1}$ 中， $A C ⊥ B C$ ，且 $A A_{1} = A B = 2$ ．下列说法正确的是（）

A、四棱锥 $B - A_{1} A C C_{1}$ 为“阳马” B、四面体 $A_{1} C_{1} C B$ 为“鳖膈” C、四棱锥 $B - A_{1} A C C_{1}$ 体积最大为 $\frac{2}{3}$ D、过 $A$ 点分别作 $A E ⊥ A_{1} B$ 于点 $E$ ， $A F ⊥ A_{1} C$ 于点 $F$ ，则 $E F ⊥ A_{1} B$

查看试题解析
12. 在发生某公共卫生事件期间，有专业机构认为该事件在一段时间没有发生大规模群体感染的标准为“连续10天，每天新增疑似病例不超过7人”，过去10天，甲、乙、丙、丁四地新增疑似病例数据信息如下：甲地：中位数为2，极差为5；乙地：平均数为2，众数为2；丙地：平均数为2，中位数为3；丁地：平均数为2，方差为2，甲、乙、丙、丁四地中，一定没有发生大规模群体感染的是（）

A、甲地 B、乙地 C、丙地 D、丁地

查看试题解析

三、填空题

13. 北京时间2月20日，北京冬奥会比赛日收官，中国代表团最终以9枚金牌4枚银牌2枚铜共15枚奖牌的总成绩，排名奖牌榜第三，创造新的历史．据统计某高校共有本科生1600人，硕士生600人，博士生200人申请报名做志愿者，现用分层抽样方法从中抽取博士生30人，则该高校抽取的志愿者总人数为．

查看试题解析
14. 我国古代认为构成宇宙万物的基本要素是金、木、水、火、土这五种物质，称为“五行”.古人构建了金生水、水生木、木生火、火生土、土生金的相生理论，随机任取“两行”，则取出的“两行”相生的概率是

查看试题解析
15. 在如图所示一组数据的茎叶图中，有一个数字被污染后模糊不清，但曾计算得该组数据的极差与中位数之和为61，则被污染的数字为.

查看试题解析
16. 如图，在 $△ A B C$ 中，D为边 $B C$ 上一点， $D C = 2 B D ， ∠ A D B = 120 ° ， A D = 2$ ，若 $△ A D C$ 的面积为 $\sqrt{3}$ ，则 $∠ B A C$ 的余弦值为．

查看试题解析

四、解答题

17. 某单位为了了解退休职工生活情况，对50名退休职工做了一次问卷调查，满分100分，并从中随机抽取了10名退休职工的问卷，得分情况统计如下：
分数
77
79
81
84
88
92
93
人数
1
1
1
3
2
1
1
试回答以下问题：

(1)、求抽取的10名退休职工问卷得分的均值和方差 $s^{2}$ .

(2)、10名退休职工问卷得分在 $\bar{x} - s$ 与 $\bar{x} + s$ 之间有多少人？这些人占10名退休职工的百分比为多少？

查看试题解析
18. 2022年2月20日，北京冬奥会在国家体育场“鸟巢”落下帷幕，中国代表团创历史最佳战绩.北京冬奥会的成功举办推动了我国冰雪运动的普及，让越来越多的青少年爱上了冰雪运动.某学校组织了一次冰雪运动趣味知识竞赛，100名喜爱冰雪运动的学生参赛，现将成绩分成 $[50 ， 60)$ ， $[60 ， 70)$ ， $[70 ， 80)$ ， $[80 ， 90)$ ， $[90 ， 100]$ （成绩均在区间 $[50 ， 100]$ 上）共五组并制成如下频率分布直方图.学校决定对成绩前15名的参赛学生进行奖励，奖品为冬奥吉祥物冰墩墩玩偶.

(1)、试求参赛学生成绩的众数及受奖励的分数线的估计值；

(2)、从受奖励的15名学生中按上述成绩分组并利用分层抽样抽取5人.现从这5人中抽取2人，试求这2人成绩恰有一个不低于90分的概率.

查看试题解析
19. 已知函数 $f (x) = 3 s i n (2 x - \frac{π}{3})$ ， $x \in R$ .

(1)、求 $f (x)$ 的最小正周期及单调增区间；

(2)、求 $f (x)$ 在区间 $[- \frac{π}{4} ， \frac{π}{4}]$ 的值域.

查看试题解析
20. 已知 $△ A B C$ 的内角A，B，C的对边分别为a，b，c，且 $b s i n C = c c o s (B - \frac{π}{6})$ .

(1)、求角B；

(2)、若b=4，求 $△ A B C$ 周长的最大值.

查看试题解析
21. 大力开展体育运动，增强学生体质，是学校教育的重要目标之一.我校开展体能测试，A、B、C三名男生准备在跳远测试中挑战2.80米的远度，已知每名男生有两次挑战机会，若第一跳成功，则等级为“优秀”，挑战结束；若第一跳失败，则再跳一次，若第二跳成功，则等级也为“优秀”，若第二跳失败，则等级为“良好”，挑战结束.已知A、B、C三名男生成功跳过2.80米的概率分别是 $\frac{2}{3}$ ， $\frac{1}{2}$ ， $\frac{1}{2}$ ，且每名男生每跳相互独立.

(1)、求A，B，C三名男生在这次跳远挑战中共跳5次的概率；

(2)、分别求A，B，C三名男生在这次跳远挑战中获得“优秀”的概率

查看试题解析
22. 如图所示，矩形 $A B C D$ 中， $A B = 3$ ， $B C = 4$ . $E$ 、 $F$ 分别在线段 $B C$ 和 $A D$ 上， $A B / / E F$ ，将矩形 $A B E F$ 沿 $E F$ 折起.记折起后的矩形为 $M N E F$ ，且平面 $M N E F ⊥$ 平面 $E C D F$ .

(1)、求证： $N C / /$ 平面 $M F D$ ；

(2)、若 $E C = 3$ ，求证： $N D ⊥ F C$ ；

(3)、求四面体 $N F E C$ 体积的最大值

查看试题解析

分数	77	79	81	84	88	92	93
人数	1	1	1	3	2	1	1