四川省凉山州2021-2022学年七年级下学期期末数学试卷

试卷更新日期：2022-08-01 类型：期末考试

进入出卷网下载

一、选择题：（本大题共12个小题，每小题2分，共24分.）

1. 如图，∠1和∠2不是同位角的是（）

A、 B、 C、 D、

查看试题解析
2. $\sqrt[3]{64}$ 的算术平方根是（）

A、4 B、±4 C、2 D、±2

查看试题解析
3. 在下列四项调查中，调查方式正确的是（）

A、了解全市中学生每天完成作业所用的时间，采用全面调查的方式 B、为保证运载火箭的成功发射，要对其所有零部件进行检查，采用抽样调查的方式 C、了解某市每天的流动人口数，采用全面调查的方式 D、了解全市中学生的视力情况，采用抽样调查的方式

查看试题解析
4. 实数a，b在数轴上对应点的位置如图所示，下列判断正确的是（）

A、|a|＜1 B、ab＞0 C、1﹣a＞1 D、a﹣b＞0

查看试题解析
5. 下列说法正确的有（）
（ 1 ）带根号的数都是无理数；（2）立方根等于本身的数是0和1；（3）﹣a一定没有平方根；（4）实数与数轴上的点是一一对应的；（5）两个无理数的差还是无理数；（6）若面积为3的正方形的边长为a，a一定是一个无理数．

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图，直线AB∥CD，C＝44°，∠AEC为直角，则∠1等于（）

A、132° B、134° C、136° D、138°

查看试题解析
7. 若 $\sqrt[3]{3} = 1.442 ， \sqrt[3]{0.3} = 0.6694$ ，那么 $\sqrt[3]{300 \times 64}$ 等于（）

A、57.68 B、115.36 C、26.776 D、53.552

查看试题解析
8. 已知点P（a+5，a﹣1）在第四象限，且到x轴的距离为2，则点P的坐标为（）

A、（4，﹣2） B、（﹣4，2） C、（﹣2，4） D、（2，﹣4）

查看试题解析
9. 甲、乙两人练习跑步，如果让乙先跑10米，甲跑5秒就追上乙；如果让乙先跑2秒，那么甲跑4秒就追上乙，若设甲、乙每秒分别跑x米，y米，下列方程组正确的是（　　）

A、 ${\begin{matrix} 5 x + 10 = 5 y \\ 4 x - 4 y = 2 \end{matrix}$ B、 ${\begin{matrix} 5 x = 5 y + 10 \\ 4 x - 2 = 4 y \end{matrix}$ C、 ${\begin{matrix} 5 x - 5 y = 10 \\ 4 (x - y) = 2 y \end{matrix}$ D、 ${\begin{matrix} 5 (x - y) = 10 \\ 4 (x - 2 y) = 2 x \end{matrix}$

查看试题解析
10. 若关于x的方程3m（x+1）+5＝m（3x﹣1）﹣5x的解是负数，则m的取值范围是（）

A、 $m ＞ - \frac{5}{4}$ B、 $m ＜ - \frac{5}{4}$ C、 $m ＞ \frac{5}{4}$ D、 $m ＜ \frac{5}{4}$

查看试题解析
11. 已知方程组 ${\begin{array}{l} 2 x + 3 y = k \\ 3 x - 4 y = k + 11 \end{array}$ 中的x，y满足5x﹣y＝3，则k＝（）

A、﹣5 B、﹣3 C、﹣6 D、﹣4

查看试题解析
12. 若规定“！”是一种数学运算符号，且1！＝1，2！＝2×1＝2，3！＝3×2×1＝6，4！＝4×3×2×1＝24，则 $\frac{100!}{98!} -$ 的值为（）

A、9900 B、991 C、 $\frac{50}{49}$ D、2

查看试题解析

二、填空题（本题共8小题，每小题3分，共24分）

13. 一个样本有10个数据：52，51，49，50，47，48，50，51，48，53，如果组距为1.5，则应分成组

查看试题解析
14. 如图，点A、B的坐标分别为（1，2）、（3，0），将△AOB沿x轴向右平移，得到△CDE，已知DB＝1，则点C的坐标为．

查看试题解析
15. 若 $(2 a + 3)^{2} + \sqrt{b - 2} = 0$ 则 $\sqrt{a^{b}} =$ .

查看试题解析
16. 若 $(m + 1) x^{m^{2}} - 3 ＞ 0$ 是关于x的一元一次不等式，则m的值为．

查看试题解析
17. 将一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G，D、C分别落在M、N的位置上，若∠EFG＝52°，则∠2﹣∠1＝°．

查看试题解析
18. 若a是介于 $\sqrt{3}$ 与 $\sqrt{7}$ 之间的整数，b是 $\sqrt{2}$ 的小数部分，则 $a b - 2 \sqrt{2}$ 的值为．

查看试题解析
19. 已知关于x的不等式组 ${\begin{array}{l} 4 x - 2 ＞ 3 x \\ x - a ＜ 7 \end{array}$ 有且只有三个整数解，则a的取值范围是．

查看试题解析
20. 将杨辉三角中的每一个数都换成分数，得到一个如图所示的分数三角形，称为莱布尼茨三角形，若用有序实数对（m，n）；表示第m行，从左到右第n个数，如（4，3）表示分数 $\frac{1}{12}$ ，则（9，2）表示的分数是．

查看试题解析

三、解答题（本大题共6小题，共52分.）

21. 计算或解方程组：

(1)、计算：（﹣2）³+|1 $- \sqrt{2}$ | $\times {(- 1)}^{2021} - \sqrt[3]{125}$ ；

(2)、解方程组： ${\begin{array}{l} 9 x + 2 y = 20 \\ 3 x + 4 y = 10 \end{array}$ ．

查看试题解析

22. 为积极响应教育部“停课不停学”的号召，某中学组织本校教师开展线上教学，为了解学生线上教学的学习效果，决定随机抽取八年级学生部分学生进行质量测评，以下是根据测试的数学成绩绘制的统计表和频数分布直方图：

	成绩x/分	频数	频率：
第1段	x＜60	2	0.04
第2段	60≤x＜70	6	0.12
第3段	70≤x＜80	9	b
第4段	80≤x＜90	a	0.36
第5段	90≤x≤100	15	0.30

请根据所给信息，解答下列问题：

(1)、a＝， b＝；

(2)、此次抽样的样本容量是 ▲ ，并补全频数分布直方图；

(3)、已知该年级有800名学生参加测试，请估计该年级数学成绩（为优秀（80分及以上）的人数．

查看试题解析

23. 如图所示，在平面直角坐标系中，点A，B的坐标分别为（a，0），B（b，0），且a，b满足 $| a + 2 | + \sqrt{b - 4} = 0$ ，点C的坐标为（0，3）．

(1)、求a，b的值及S_△ABC；

(2)、若点M在x轴上，且 $S_{A O C} = \frac{1}{3} S_{A B C}$ ，试求点M的坐标．

查看试题解析
24. “冰墩墩”和“雪容融”分别是北京2022年冬奥会和冬残奥会的吉祥物．自2019年正式亮相后，相关特许商品投放市场，持续热销．某冬奥官方特许商品零售店购进了一批同一型号的“冰墩墩”和“雪容融”玩具，连续两个月的销售情况如表：
月份
销售量/件
销售额/元
冰墩墩
雪容融
第1个月
100
40
14800
第2个月
160
60
23380

(1)、求此款“冰墩墩”和“雪容融”玩具的零售价格；

(2)、某单位欲购买这两款玩具作为冬奥知识竞赛活动的奖品，要求“雪容融”的数量恰好等于“冰墩墩”的数量的2倍，且购买总资金不得超过9000元，请根据要求确定该单位购买“冰墩墩”玩具的最大数量．

查看试题解析
25. 若不等式（组）①的解集中的任意解都满足不等式（组）②，则称不等式（组）①被不等式（组）②覆盖．特别地，若一个不等式（组）无解，则它被其他任意不等式（组）覆盖．
例如：不等式x＞1被不等式x＞0覆盖；不等式组 ${\begin{array}{l} 2 x - 1 ＞ 0 \\ - x ＞ 0 \end{array}$ 无解，被其他任意不等式（组）覆盖．

(1)、下列不等式（组）中，能被不等式x＜﹣3覆盖的是（）．

A、3x﹣2＜0； B、﹣2x+2＜0； C、﹣19＜2x＜﹣6； D、 ${\begin{array}{l} - 3 x ＜ - 8 \\ 4 - x ＜ 3 \end{array}$ ．

(2)、若关于x的不等式3x﹣m＞5x﹣4m被x≤3覆盖，求m的取值范围．

(3)、若关于x的不等式m﹣2＜x＜﹣2m﹣3被x＞2m+3覆盖，直接写出m的取值范围：．

查看试题解析
26. 已知：如图1，直线AB、CD被直线MN所截，且AB∥CD，点E在直线AB、CD之间的线段MN上，P、Q分别在直线AB、CD上，连接PE、EQ．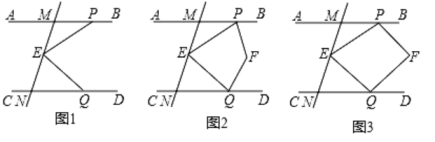

(1)、小明探究发现：∠PEQ＝∠APE+∠CQE，请你帮小明说明理由；

(2)、如图2，已知 $∠ F P B = \frac{1}{2} ∠ E P B ， ∠ F Q D = \frac{1}{2} ∠ E Q D$ ，若∠PEQ＝80°请你利用小明发现的结论求∠PFQ的度数；

(3)、如图3，若 $∠ F P B = \frac{1}{3} ∠ E P B ， ∠ F Q D = \frac{1}{3} ∠ E Q D$ ，请你直接写出∠PEQ和∠PFQ之间的数量关系．

查看试题解析

月份	销售量/件		销售额/元
月份	冰墩墩	雪容融	销售额/元
第1个月	100	40	14800
第2个月	160	60	23380