江苏省盐城市2022年中考数学试卷
试卷更新日期:2022-08-01 类型:中考真卷
一、单选题
-
1. 2022的倒数是( )A、2022 B、-2022 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 下列四幅照片中,主体建筑的构图不对称的是( )A、
 B、
B、 C、
C、 D、
D、 4. 盐城市图书馆现有馆藏纸质图书1600000余册.数据1600000用科学记数法表示为( )A、 B、 C、 D、5. 一组数据-2,0,3,1,-1的极差是( )A、2 B、3 C、4 D、56. 正方体的每个面上都有一个汉字,如图是它的一种平面展开图,那么在原正方体中,与“盐”字所在面相对的面上的汉字是( )
4. 盐城市图书馆现有馆藏纸质图书1600000余册.数据1600000用科学记数法表示为( )A、 B、 C、 D、5. 一组数据-2,0,3,1,-1的极差是( )A、2 B、3 C、4 D、56. 正方体的每个面上都有一个汉字,如图是它的一种平面展开图,那么在原正方体中,与“盐”字所在面相对的面上的汉字是( ) A、强 B、富 C、美 D、高7. 小明将一块直角三角板摆放在直尺上,如图所示,则与的关系是( )
A、强 B、富 C、美 D、高7. 小明将一块直角三角板摆放在直尺上,如图所示,则与的关系是( )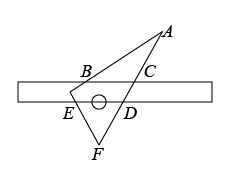 A、互余 B、互补 C、同位角 D、同旁内角8. “跳眼法”是指用手指和眼睛估测距离的方法
A、互余 B、互补 C、同位角 D、同旁内角8. “跳眼法”是指用手指和眼睛估测距离的方法步骤:
第一步:水平举起右臂,大拇指紧直向上,大臂与身体垂直;
第二步:闭上左眼,调整位置,使得右眼、大拇指、被测物体在一条直线上;
第三步:闭上右眼,睁开左眼,此时看到被测物体出现在大拇指左侧,与大拇指指向的位置有一段横向距离,参照被测物体的大小,估算横向距离的长度;
第四步:将横向距离乘以10(人的手臂长度与眼距的比值一般为10),得到的值约为被测物体离观测,点的距离值.
如图是用“跳眼法”估测前方一辆汽车到观测点距离的示意图,该汽车的长度大约为4米,则汽车到观测点的距离约为( )
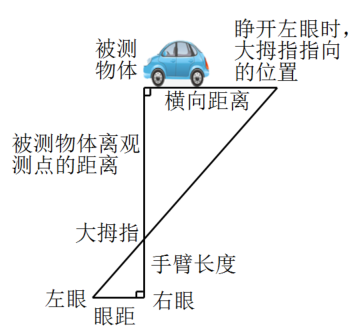 A、40米 B、60米 C、80米 D、100米
A、40米 B、60米 C、80米 D、100米二、填空题
-
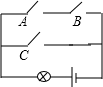
9. 使 有意义的x的取值范围是 .10. 已知反比例函数的图象过点(2,3),则该函数的解析式为 .11. 分式方程的解为 .12. 如图所示,电路图上有A,B,C三个开关和一个小灯泡,闭合开关C或者同时闭合开关A,B,都可使小灯泡发光.现任意闭合其中一个开关,则小灯泡发光的概率等于
 13. 如图,、是的弦,过点A的切线交的延长线于点 , 若 , 则°.
13. 如图,、是的弦,过点A的切线交的延长线于点 , 若 , 则°.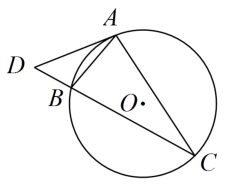 14. 如图,在矩形中, , 将线段绕点按逆时针方向旋转,使得点落在边上的点处,线段扫过的面积为 .
14. 如图,在矩形中, , 将线段绕点按逆时针方向旋转,使得点落在边上的点处,线段扫过的面积为 . 15. 若点在二次函数的图象上,且点到轴的距离小于2,则的取值范围是 .16. 《庄子▪天下篇》记载“一尺之锤,日取其半,万世不竭.”如图,直线与轴交于点 , 过点作轴的平行线交直线于点 , 过点作轴的平行线交直线于点 , 以此类推,令 , , , , 若对任意大于1的整数恒成立,则的最小值为 .
15. 若点在二次函数的图象上,且点到轴的距离小于2,则的取值范围是 .16. 《庄子▪天下篇》记载“一尺之锤,日取其半,万世不竭.”如图,直线与轴交于点 , 过点作轴的平行线交直线于点 , 过点作轴的平行线交直线于点 , 以此类推,令 , , , , 若对任意大于1的整数恒成立,则的最小值为 .
三、解答题
-
17. .18. 解不等式组: .19. 先化简,再求值: , 其中 .20. 某社区举行新冠疫情防控核酸检测大演练,卫生防疫部门在该社区设置了三个核酸检测点A、B、C,甲、乙两人任意选择一个检测点参加检测.求甲、乙两人不在同一检测点参加检测的概率.(用画树状图或列表的方法求解)21. 小丽从甲地匀速步行去乙地,小华骑自行车从乙地匀速前往甲地,同时出发,两人离甲地的距离(m)与出发时间(min)之间的函数关系如图所示.
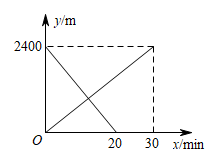 (1)、小丽步行的速度为m/min;(2)、当两人相遇时,求他们到甲地的距离.22. 证明:垂直于弦的直径平分弦以及弦所对的两条弧.
(1)、小丽步行的速度为m/min;(2)、当两人相遇时,求他们到甲地的距离.22. 证明:垂直于弦的直径平分弦以及弦所对的两条弧. 23. 如图,在与中,点、分别在边、上,且 , 若 ▲ , 则 . 请从①;②;③这三个选项中选择一个作为条件(写序号),并加以证明.
23. 如图,在与中,点、分别在边、上,且 , 若 ▲ , 则 . 请从①;②;③这三个选项中选择一个作为条件(写序号),并加以证明.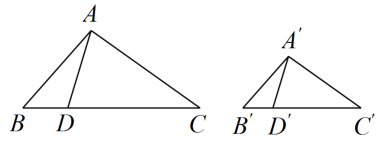 24. 合理的膳食可以保证青少年体格和智力的正常发育.综合实践小组为了解某校学生膳食营养状况,从该校1380名学生中调查了100名学生的膳食情况,调查数据整理如下:
24. 合理的膳食可以保证青少年体格和智力的正常发育.综合实践小组为了解某校学生膳食营养状况,从该校1380名学生中调查了100名学生的膳食情况,调查数据整理如下:
中国营养学会推荐的三大营养素供能比参考值
蛋白质
10%~15%
脂肪
20%~30%
碳水化合物
50%~65%
注:供能比为某物质提供的能量占人体所需总能量的百分比.
(1)、本次调查采用的调查方法;(填“普查”或“抽样调查”)(2)、通过对调查数据的计算,样本中的蛋白质平均供能比约为14.6%,请计算样本中的脂肪平均供能比和碳水化合物平均供能比;(3)、结合以上的调查和计算,对照下表中的参考值,请你针对该校学生膳食状况存在的问题提一条建议.25. 2022年6月5日,“神舟十四号”载人航天飞船搭载“明星”机械臂成功发射.如图是处于工作状态的某型号手臂机器人示意图,是垂直于工作台的移动基座,、为机械臂,m,m,m, . 机械臂端点到工作台的距离m.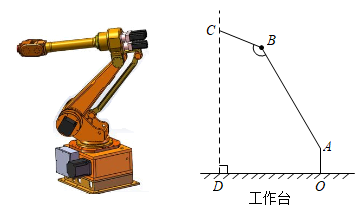 (1)、求、两点之间的距离;(2)、求长.(结果精确到0.1m,参考数据: , , , )26. 【经典回顾】
(1)、求、两点之间的距离;(2)、求长.(结果精确到0.1m,参考数据: , , , )26. 【经典回顾】梅文鼎是我国清初著名的数学家,他在《勾股举隅》中给出多种证明勾股定理的方法图1是其中一种方法的示意图及部分辅助线.

在中, , 四边形、和分别是以的三边为一边的正方形.延长和 , 交于点 , 连接并延长交于点 , 交于点 , 延长交于点 .
(1)、证明:;(2)、证明:正方形的面积等于四边形的面积;(3)、请利用(2)中的结论证明勾股定理.(4)、【迁移拓展】如图2,四边形和分别是以的两边为一边的平行四边形,探索在下方是否存在平行四边形 , 使得该平行四边形的面积等于平行四边形、的面积之和.若存在,作出满足条件的平行四边形(保留适当的作图痕迹);若不存在,请说明理由.
27. 【发现问题】小明在练习簿的横线上取点为圆心,相邻横线的间距为半径画圆,然后半径依次增加一个间距画同心圆,描出了同心圆与横线的一些交点,如图1所示,他发现这些点的位置有一定的规律.
【提出问题】
小明通过观察,提出猜想:按此步骤继续画圆描点,所描的点都在某二次函数图象上.


 (1)、【分析问题】
(1)、【分析问题】小明利用已学知识和经验,以圆心为原点,过点的横线所在直线为轴,过点且垂直于横线的直线为轴,相邻横线的间距为一个单位长度,建立平面直角坐标系,如图2所示.当所描的点在半径为5的同心圆上时,其坐标为 .
(2)、【解决问题】请帮助小明验证他的猜想是否成立.
(3)、【深度思考】小明继续思考:设点 , 为正整数,以为直径画 , 是否存在所描的点在上.若存在,求的值;若不存在,说明理由.