湖南省怀化市新晃县城区2021-2022学年八年级下学期期末质量检测数学试卷

试卷更新日期：2022-08-01 类型：期末考试

进入出卷网下载

一、单选题

1. 点A（﹣5，3）所在的象限是（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下列四组数据不能作为直角三角形的三边长的是（）

A、3，4，5 B、 $\sqrt{2}$ ， $\sqrt{3}$ ， $\sqrt{5}$ C、6，8，10 D、2，4，6

查看试题解析
3. 一个n边形的内角和为720°，则n等于（）

A、4 B、5 C、6 D、7

查看试题解析
4. 下列函数中，正比例函数是（）

A、 $y = 2 x^{2}$ B、 $y = - 6 x - 1$ C、 $y = - \frac{5}{x}$ D、 $y = - 5 x$ .

查看试题解析
5. 在下列图形中，既是中心对称图形，又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
6. 如图，在平行四边形ABCD中，∠ABC的角平分线交边AD于点E，∠C＝130°，则∠AEB的度数是（）

A、20° B、25° C、30° D、35°

查看试题解析
7. 若一次函数 $y = k x + b$ 的图象如图所示，则下列说法正确的是（）

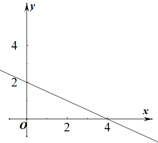A、 $k > 0$ B、 $b = 2$ C、y随x的增大而增大 D、 $x = 3$ 时， $y = 0$

查看试题解析
8. “早发现，早报告，早隔离，早治疗”是我国抗击“新冠肺炎”的宝贵经验，其中“早”字出现的频率是（）

A、 $\frac{1}{12}$ B、 $\frac{1}{4}$ C、 $\frac{2}{3}$ D、 $\frac{1}{3}$

查看试题解析
9. 在四边形ABCD中，AB＝DC，AD＝BC.请再添加一个条件，使四边形ABCD是矩形.添加的条件不能是(　　)

A、AB∥DC B、∠A＝90° C、∠B＝90° D、AC＝BD

查看试题解析
10. 如图，在Rt△ABC中，∠BAC=90°，D，E分别是AB，BC的中点，F在CA延长线上，∠FDA=∠B，AC=6，AB=8，则四边形AEDF的周长为（）

A、16 B、20 C、18 D、22

查看试题解析
11. 甲、乙两人在一次跨栏比赛中，路程s（m）与时间t（s）的函数关系如图所示，根据图形下列说法正确的个数为（）
①这次比赛的赛程是110米②甲先到达终点；③乙在这次比赛中的平均速度为 $\frac{55}{7}$ m/s；④乙的平均速度比甲快

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

12. 点 P（3，﹣4）关于 y 轴对称点的坐标是．

查看试题解析
13. 一次函数 $y = x - 1$ 的图象不经过第象限.

查看试题解析
14. 在Rt△ABC中，∠C=90°，∠A=60°，BC=10，则AC=.

查看试题解析
15. 某班50位同学中，1月份出生的频率是0.3，这个班1月份出生的同学有人．

查看试题解析
16. 如图，依次连接第一个矩形各边的中点得到一个菱形，再依次连接菱形各边的中点得到第二个矩形，按照此方法继续下去.已知第一个矩形的面积为1，则第n个矩形的面积为.

查看试题解析

三、解答题

17. 已知正比例函数的图象经过点A（ $- 1$ ， 5）.

(1)、求这个函数表达式。

(2)、点B（2，10）、C（ $- 3$ ， 15）是否在这个函数的图象上？

查看试题解析
18. 如图，已知A $(- 2 ， 3)$ 及B $(- 2 ， - 2)$ 是正方形ABCD的两个顶点，正方形与x轴相交于点E和点G，与y轴相交于点F和点H.

(1)、写出点F、C、G、D的坐标.

(2)、图中D点在O点的北偏东 $45 °$ 的方向上，与O点的距离为 $3 \sqrt{2}$ .请类似的写出点B、点H分别在O点的什么方向上，以及到O点的距离.

查看试题解析
19. 已知：如图，在矩形ABCD中，点E在边AB上，点F在边BC上，且BE=CF， EF=DF.

(1)、求证：△EBF≌△FCD

(2)、判断△EFD是什么三角形？说明理由。

查看试题解析

20. 某校举行以“建党一百周年”为主题的图片制作比赛，赛后整理参赛同学的成绩，并制作成图表如下：

分数段	频数	频率
60≤x＜70	30	0.15
70≤x＜80	m	0.45
80≤x＜90	60	n
90≤x＜100	20	0.1

请根据以如图表提供的信息，解答下列问题．

(1)、求表中m和n所表示的数；

(2)、请在图中补全频数分布直方图；

(3)、若比赛成绩不低于80分可以获奖，则获奖率为多少？

查看试题解析

21. 如图，点N(0，6)，点M在x轴负半轴上，ON＝3OM.A为线段MN上一点，AB⊥x轴，垂足为点B，AC⊥y轴，垂足为点C.

(1)、写出点M的坐标；

(2)、求直线MN的表达式；

(3)、若点A的横坐标为－1，求矩形ABOC的面积.

查看试题解析
22. 如图，在矩形ABCD中，过对角线AC的中点O作垂线EF交边BC，AD分别为点E，F，连接AE，CF.

(1)、求证：四边形AECF是菱形；

(2)、若AD＝8，AB＝4，求CF的长.

查看试题解析
23. 由于疫情的影响，“地摊经济”成为了很多人经济来源的一种形式．李叔叔从市场得知如下信息：

A商品

B商品

进价（元/件）

35

5

售价（元/件）

45

8

李叔叔计划购进A、B商品共100件进行销售．设购进A商品x件，A、B商品全部销售完后获得利润为y元．

(1)、求出y与x之间的函数关系式；

(2)、若李叔叔用不超过2000元资金一次性购进A，B两种商品，则如何进货，才能使得获利最大？并求出最大利润．

查看试题解析
24. 如图，点P是正方形ABCD内的一点，连接CP，将线段CP绕点C顺时针旋转90°，得到线段CQ，连接BP，DQ．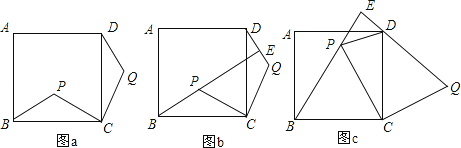

(1)、如图a，求证：△BCP≌△DCQ；

(2)、如图，延长BP交直线DQ于点E．
①如图b，求证：BE⊥DQ；
②如图c，若△BCP为等边三角形，判断△DEP的形状，并说明理由．

查看试题解析

	A商品	B商品
进价（元/件）	35	5
售价（元/件）	45	8