斜率型定值型问题-2023年高考数学之解密圆锥曲线命题点对点突破（全国通用）

试卷更新日期：2022-07-30 类型：一轮复习

进入出卷网下载

一、斜率问题

1. 已知，椭圆 $C$ 过点 $A (1 ， \frac{3}{2})$ ，两个焦点为 $(- 1 ， 0) ， (1 ， 0)$ .
（Ⅰ）求椭圆 $C$ 的方程；

（Ⅱ） $E ， F$ 是椭圆 $C$ 上的两个动点，如果直线 $A E$ 的斜率与 $A F$ 的斜率互为相反数，证明直线 $E F$ 的斜率为定值，并求出这个定值．

查看试题解析
2. 已知椭圆C的中心在原点，一个焦点 $F = (0 ， \sqrt{2})$ ，且长轴长与短轴长的比是 $\sqrt{2} ： 1$ ．
（Ⅰ）求椭圆C的方程；

（Ⅱ）若椭圆C在第一象限的一点P的横坐标为1，过点P作倾斜角互补的两条不同的直线PA，PB分别交椭圆C于另外两点A，B，求证：直线AB的斜率为定值；

（Ⅲ）在（Ⅱ）的条件下，求△PAB面积的最大值．

查看试题解析
3. 如图，已知点 $P (2 ， 2)$ 是抛物线 $C$ ： $y^{2} = 2 x$ 上一点，过点 $P$ 作两条斜率相反的直线分别与抛物线交于 $A$ 、 $B$ 两点，直线 $P A$ 的斜率为 $k (k > 0)$ .

（Ⅰ）若直线 $P A$ 、 $P B$ 恰好为圆 ${(x - 2)}^{2} + y^{2} = 1$ 的切线，求直线 $P A$ 的斜率；

（Ⅱ）求证：直线 $A B$ 的斜率为定值.并求出当 $△ P A B$ 为直角三角形时， $△ P A B$ 的面积.

查看试题解析

二、斜率之和问题

4. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率 $e = \frac{1}{3}$ ，且椭圆 $C$ 经过点 $P (- 1 ， - \frac{8}{3})$ ．

(1)、求椭圆 $C$ 的方程．

(2)、不过点 $P$ 的直线 $l$ ： $y = k x + 3$ 与椭圆 $C$ 交于 $A$ ， $B$ 两点，记直线 $P A$ ， $P B$ 的斜率分别为 $k_{1}$ ， $k_{2}$ ，试判断 $k_{1} + k_{2}$ 是否为定值．若是，求出该定值：若不是，请说明理由．

查看试题解析
5. 已知抛物线 $E ： y^{2} = 2 p x (p > 0)$ ，点 $P (2 ， 2 \sqrt{2})$ 在抛物线 $E$ 上.

(1)、求抛物线 $E$ 的准线方程；

(2)、过点 $Q (- 2 ， 0)$ 的直线 $l$ 与抛物线 $E$ 交于 $A ， B$ 两点，直线 $P A$ 交 $y$ 轴于点 $M$ ，直线 $P B$ 交 $y$ 轴于 $N$ ，记直线 $Q M ， Q N$ 的斜率分别为 $k_{1} ， k_{2}$ ，求证： $k_{1} + k_{2}$ 为定值.

查看试题解析
6. 如图，椭圆 $E ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 经过点 $A (0 ， - 1)$ ，且离心率为 $\frac{\sqrt{2}}{2}$ .
(I)求椭圆 $E$ 的方程；

(II)经过点 $(1 ， 1)$ ，且斜率为 $k$ 的直线与椭圆 $E$ 交于不同两点 $P ， Q$ （均异于点 $A$ ），

问：直线 $A P$ 与 $A Q$ 的斜率之和是否为定值？若是，求出此定值；若否，说明理由．

查看试题解析
7. 已知椭圆 $C$ ： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $(a > b > 0)$ 的上顶点 $A$ 与下顶点 $B$ 在直线 $l$ ： $x - 2 y + 1 = 0$ 的两侧，且点 $B$ 到 $l$ 的距离是 $A$ 到 $l$ 的距离的3倍．
（Ⅰ）求 $b$ 的值；

（Ⅱ）设 $C$ 与 $l$ 交于 $P$ ， $Q$ 两点，求证：直线 $B P$ 与 $B Q$ 的斜率之和为定值．

查看试题解析
8. 已知圆 $C$ 和 $y$ 轴相切于点 $T (0 ， 2)$ ，与 $x$ 轴的正半轴交于 $M$ 、 $N$ 两点（ $M$ 在 $N$ 的左侧），且 $M N = 3$ .
（Ⅰ）求圆 $C$ 的方程；

（Ⅱ）过点 $M$ 任作一条直线与圆 $O$ ： $x^{2} + y^{2} = 4$ 相交于点 $A$ 、 $B$ ，连接 $A N$ 和 $B N$ ，记 $A N$ 和 $B N$ 的斜率分别为 $k_{1}$ ， $k_{2}$ ，求证： $k_{1} + k_{2}$ 为定值.

查看试题解析
9. 椭圆C: $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ (a>b>0)的左、右焦点分别为 $F_{1}, F_{2}$ ，离心率为 $\frac{\sqrt{3}}{2}$ ，过焦点 $F_{2}$ 且垂直于x轴的直线被椭圆C截得的线段长为1．
（Ⅰ）求椭圆C的方程；

（Ⅱ）已知点M（0，-1），直线l经过点N（2，1）且与椭圆C相交于A,B两点（异于点M），记直线MA的斜率为 $k_{1}$ ，直线MB的斜率为 $k_{2}$ ，证明 $k_{1} + k_{2}$ 为定值，并求出该定值.

查看试题解析
10. 已知：点 $A (1 ， \sqrt{2})$ 是离心率为 $\frac{\sqrt{2}}{2}$ 的椭圆 $C$ ： $\frac{y^{2}}{a^{2}} + \frac{x^{2}}{b^{2}} = 1 (a > b > 0)$ 上的一点．斜率为 $\sqrt{2}$ 的直线BD交椭圆C于B、D两点，且A、B、D三点不重合．

（Ⅰ）求椭圆C的方程；

（Ⅱ）△ABD的面积是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由？

（Ⅲ）求证：直线AB、AD的斜率之和为定值．

查看试题解析
11. 已知椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （ $a > b > 0$ ）的焦距为2，离心率为 $\frac{\sqrt{2}}{2}$ ，右顶点为 $A$ .
（I）求该椭圆的方程；

（II）过点 $D (\sqrt{2}, - \sqrt{2})$ 作直线 $P Q$ 交椭圆于两个不同点 $P 、 Q$ ，求证：直线 $A P$ ， $A Q$ 的斜率之和为定值.

查看试题解析

三、斜率之差问题

12. 椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率 $e = \frac{\sqrt{3}}{2}$ ， $a + b = 3$ ．

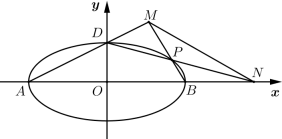(1)、求椭圆C的方程；

(2)、如图，A，B，D是椭圆C的顶点，P是椭圆C上除顶点外的任意一点，直线DP交x轴于点N，直线AD交BP于点M，设MN的斜率为m，BP的斜率为n，证明： $2 m - n$ 为定值．

查看试题解析

四、斜率之积问题

13. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{1}{2}$ ，点 $A (1 ， \frac{3}{2})$ 在椭圆C上．

(1)、求椭圆C的方程；

(2)、若椭圆C的右顶点为B，直线l过定点 $M (3 ， 0)$ ，且交椭圆 $C$ 于P，Q两点（异于点B），试探究直线 $B P$ 与 $B Q$ 的斜率的乘积是否为定值？若是，求出定值；若不是，请说明理由．

查看试题解析
14. 如图，在直角坐标系 $x O y$ 中，圆 $O ： x^{2} + y^{2} = 4$ 与 $x$ 轴负半轴交于点 $A$ ，过点 $A$ 的直线 $A M$ ， $A N$ 分别与圆 $O$ 交于 $M$ ， $N$ 两点．

（Ⅰ）若 $k_{A M} = 2$ ， $k_{A N} = - \frac{1}{2}$ ，求 $△ A M N$ 的面积；

（Ⅱ）若直线 $M N$ 过点 $(1 ， 0)$ ，证明： $k_{A M} \cdot k_{A N}$ 为定值，并求此定值．

查看试题解析
15. 设 $P (x, y)$ 是椭圆 $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ 上的点且 $P$ 的纵坐标 $y \neq 0$ ，点 $A (- 5, 0)$ 、 $B (5, 0)$ ，试判断 $k_{P A} \cdot k_{P B}$ 是否为定值？若是定值，求出该定值；若不是定值，请说明理由．

查看试题解析
16. 设 $P (x ， y)$ 是椭圆 $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ 上的点且 $P$ 的纵坐标 $y \neq 0$ ，点 $A (- 5 ， 0)$ 、 $B (5 ， 0)$ ，试判断 $k_{P A} \cdot k_{P B}$ 是否为定值？若是定值，求出该定值；若不是定值，请说明理由．

查看试题解析

五、斜率之商问题

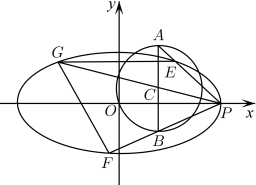
17. 如图，已知椭圆 $Γ ： \frac{x^{2}}{4} + y^{2} = 1$ 和圆 $C ： (x - 4 t)^{2} + (y - 3 t)^{2} = 25 t^{2} (0 < t < \frac{1}{2})$ ，直线 $l ： x = 4 t$ 交圆于上下两点A，B，点P为椭圆的右顶点， $P A ， P B ， P C$ 分别交椭圆于E，F，G，记 $P A ， P B$ 的斜率分别为 $k_{1} ， k_{2}$ .

(1)、求 $\frac{k_{1}}{k_{2}}$ 的值；

(2)、记 $△ P F G$ 和 $△ P E G$ 的面积分别为 $S_{1} ， S_{2}$ ，若 $S_{1} = 4 S_{2}$ ，求t的值.

查看试题解析
18. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点分别为 $F_{1} ， F_{2}$ ，点 $D$ 为线段 $F_{1} O$ 的中点，过 $F_{2}$ 的直线 $l$ 与 $C$ 的右支交于 $M (x_{1} ， y_{1}) ， N (x_{2} ， y_{2})$ 两点，延长 $M D ， N D$ 分别与 $C$ 交于点 $P ， Q$ 两点，若 $C$ 的离心率为 $\sqrt{2} ， (3 ， \sqrt{7})$ 为 $C$ 上一点.

(1)、求证： $x_{1} y_{2} - x_{2} y_{1} = 2 (y_{2} - y_{1})$ ；

(2)、已知直线 $l$ 和直线 $P Q$ 的斜率都存在，分别记为 $k_{1} ， k_{2} ， k_{1} \neq 0$ ，判断 $\frac{k_{2}}{k_{1}}$ 是否为定值？若是，求出该定值；若不是，说明理由.

查看试题解析
19. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的右焦点为F，长轴长为4，离心率为 $\frac{1}{2}$ ．过点 $Q (4 ， 0)$ 的直线 $l$ 与椭圆C交于A，B两点．

(1)、求椭圆C的标准方程；

(2)、设直线 $A F ， B F$ 的斜率分别为 $k_{1} ， k_{2} (k_{2} \neq 0)$ ，求证： $\frac{k_{1}}{k_{2}}$ 为定值．

查看试题解析
20. 在平面直角坐标系中， $A_{1}$ ， $A_{2}$ 两点的坐标分别为 $(- 2 ， 0)$ ， $(2 ， 0)$ ，直线 $A_{1} M$ ， $A_{2} M$ ．相交于点M且它们的斜率之积是 $- \frac{3}{4}$ ，记动点M的轨迹为曲线E．过点 $F (1 ， 0)$ 作直线l交曲线E于P，Q两点，且点P位于x轴上方．记直线 $A_{1} Q$ ， $A_{2} P$ 的斜率分别为 $k_{1}$ ， $k_{2}$ ．

(1)、证明： $\frac{k_{1}}{k_{2}}$ 为定值：

(2)、设点Q关于x轴的对称点为 $Q_{1}$ ，求 $△ P F Q_{1}$ 面积的最大值．

查看试题解析
21. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的长轴长为4，焦距为 $2 \sqrt{2}$
（Ⅰ）求椭圆 $C$ 的方程；

（Ⅱ）过动点 $M (0 ， m) (m > 0)$ 的直线交 $x$ 轴与点 $N$ ，交 $C$ 于点 $A ， P$ ( $P$ 在第一象限)，且 $M$ 是线段 $P N$ 的中点.过点 $P$ 作 $x$ 轴的垂线交 $C$ 于另一点 $Q$ ，延长 $Q M$ 交 $C$ 于点 $B$ .

（ⅰ）设直线 $P M ， Q M$ 的斜率分别为 $k_{1} ， k_{2}$ ，证明 $\frac{k_{2}}{k_{1}}$ 为定值；

（ⅱ）求直线 $A B$ 的斜率的最小值.

查看试题解析

六、斜率综合问题

22. 如图.矩形ABCD的长 $A B = 2 \sqrt{3}$ ，宽 $B C = \frac{1}{2}$ ，以A､B为左右焦点的椭圆 $M ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ 恰好过C､D两点，点P为椭圆M上的动点.

(1)、求椭圆M的方程，并求 $\vec{P A} \cdot \vec{P B}$ 的取值范围；

(2)、若过点B且斜率为k的直线交椭圆于M､N两点（点C与M､N两点不重合），且直线CM､CN的斜率分别为 $k_{1} 、 k_{2}$ ，试证明 $k_{1} + k_{2} - 2 k$ 为定值.

查看试题解析
23. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{3}}{2} ， P (2 ， 1)$ 为椭圆 $C$ 上一点.

(1)、求椭圆 $C$ 的标准方程.

(2)、若过点 $Q (2 ， 0)$ 且斜率为 $k$ 的直线 $l$ 与椭圆 $C$ 相交于 $A ， B$ 两点，记直线 $A P ， B P$ 的斜率分别为 $k_{1} ， k_{2}$ ，试问 $k_{1} + k_{2} - 2 k$ 是否是定值？若是，求出此定值；若不是，请说明理由.

查看试题解析