2023年全国甲卷(文数)模拟题
试卷更新日期:2022-07-29 类型:高考模拟
一、单选题
-
1. 已知集合 , , 则=( )A、 B、 C、 D、{1}2. 耀华中学全体学生参加了主题为“致敬建党百年,传承耀华力量”的知识竞赛,随机抽取了400名学生进行成绩统计,发现抽取的学生的成绩都在50分至100分之间,进行适当分组后(每组为左闭右开的区间),画出频率分布直方图如图所示,下列说法正确的是( )
 A、直方图中x的值为0.004 B、在被抽取的学生中,成绩在区间的学生数为30人 C、估计全校学生的平均成绩为84分 D、估计全校学生成绩的样本数据的80%分位数约为93分3. 已知复数z满足 , 且 , 则( )A、 B、 C、2 D、4. 某几何体的三视图如图所示,则该几何体的体积是( )
A、直方图中x的值为0.004 B、在被抽取的学生中,成绩在区间的学生数为30人 C、估计全校学生的平均成绩为84分 D、估计全校学生成绩的样本数据的80%分位数约为93分3. 已知复数z满足 , 且 , 则( )A、 B、 C、2 D、4. 某几何体的三视图如图所示,则该几何体的体积是( ) A、 B、 C、 D、5. 将函数的图象分别向左、向右各平移个单位长度后,所得的两个图象对称中心重合,则的最小值为( )A、 B、2 C、3 D、66. 某高校计划派出甲、乙、丙3名男生和A,B,C,3名女性共6名志愿者参与北京冬奥会志愿者工作,现将他们分配到北京、延庆2个赛区进行培训,其中1名男性志愿者和1名女性志愿者去北京赛区,其他都去延庆赛区,则甲和A被选去北京赛区培训的概率为( )A、 B、 C、 D、7. 函数的图像大致为( )A、
A、 B、 C、 D、5. 将函数的图象分别向左、向右各平移个单位长度后,所得的两个图象对称中心重合,则的最小值为( )A、 B、2 C、3 D、66. 某高校计划派出甲、乙、丙3名男生和A,B,C,3名女性共6名志愿者参与北京冬奥会志愿者工作,现将他们分配到北京、延庆2个赛区进行培训,其中1名男性志愿者和1名女性志愿者去北京赛区,其他都去延庆赛区,则甲和A被选去北京赛区培训的概率为( )A、 B、 C、 D、7. 函数的图像大致为( )A、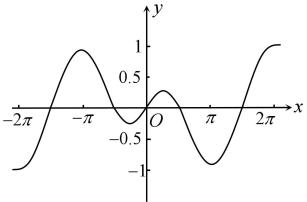 B、
B、 C、
C、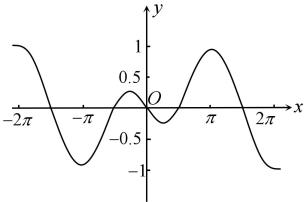 D、
D、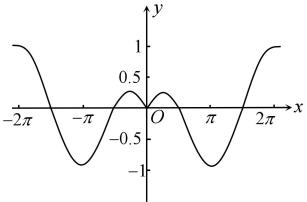 8. 已知函数至多有2个不同的零点,则实数a的最大值为( ).A、0 B、1 C、2 D、e9. 在正方体 中,设直线 与直线AD所成的角为 ,直线 与平面 所成的角为 ,则 ( )A、 B、 C、 D、10. 在三棱锥中,为等腰直角三角形, , 为正三角形,且二面角的平面角为 , 则三棱锥的外接球表面积为( )A、 B、 C、 D、11. 已知双曲线的右焦点为F,左顶点为A,过F的直线交双曲线C于P、Q两点,连接、 , 分别与直线交于M、N两点,若 , 则( )A、21 B、9 C、21或 D、21或912. 实数 , , 分别满足 , , , 则 , , 的大小关系为( )A、 B、 C、 D、
8. 已知函数至多有2个不同的零点,则实数a的最大值为( ).A、0 B、1 C、2 D、e9. 在正方体 中,设直线 与直线AD所成的角为 ,直线 与平面 所成的角为 ,则 ( )A、 B、 C、 D、10. 在三棱锥中,为等腰直角三角形, , 为正三角形,且二面角的平面角为 , 则三棱锥的外接球表面积为( )A、 B、 C、 D、11. 已知双曲线的右焦点为F,左顶点为A,过F的直线交双曲线C于P、Q两点,连接、 , 分别与直线交于M、N两点,若 , 则( )A、21 B、9 C、21或 D、21或912. 实数 , , 分别满足 , , , 则 , , 的大小关系为( )A、 B、 C、 D、二、填空题
-
13. 已知向量 , , 若 , 则 .14. 点 在圆 : 上, , ,则 最大时, .15. 已知抛物线的焦点为F,P为抛物线上一动点,点 , 当的周长最小时,点P的坐标为 .16. 在△中,角 , , 所对的边分别为 , , . 若 , , 则△面积的最小值是 .
三、解答题
-
17. 新生儿的某种疾病要接种三次疫苗进行免疫,假设三次接种之间互不影响,每人每次接种成功的概率相等.为了解新生儿该疫苗接种剂量与接种成功之间的关系,现进行了两种接种方案的临床试验:10∕次剂量组与20∕次剂量组,接种三次后的试验结果如下:
单位:人
接种方案
结果
合计
接种成功
接种不成功
10∕次剂量组
900
100
1000
20∕次剂量组
973
27
1000
合计
1873
127
2000
(1)、根据数据说明哪种接种方案效果好,并依据的独立性检验,判断能否认为该疫苗是否接种成功与接种方案有关;(2)、以频率代替概率,若选用接种效果好的方案,参与该试验的1000人此剂量接种三次的成功人数比只接种一次的成功人数平均提高多少?18. 设数列的各项均为正数,前n项和为 , 满足 .(1)、求的通项公式;(2)、设 , 的前n项和为 , 求证: .19. 如图所示,四棱锥 , 底面在以AC为直径的圆O上,PO⊥圆O,为等边三角形, , . (1)、求证:平面PBD⊥平面PAB;(2)、线段PB上是否存在一点M使得直线PA与平面AMC所成角的正弦值为?若存在,求出;若不存在,请说明理由.20. 已知函数 .(1)、若时,过点作曲线的切线l,求l的方程;(2)、若函数在处取极小值,求a的取值范围.21. 已知椭圆:的左顶点为 , 圆:经过椭圆的上、下顶点.(1)、求椭圆的方程和焦距;(2)、已知 , 分别是椭圆和圆上的动点( , 不在坐标轴上),且直线与轴平行,线段的垂直平分线与轴交于点 , 圆在点处的切线与轴交于点.求线段长度的最小值.
(1)、求证:平面PBD⊥平面PAB;(2)、线段PB上是否存在一点M使得直线PA与平面AMC所成角的正弦值为?若存在,求出;若不存在,请说明理由.20. 已知函数 .(1)、若时,过点作曲线的切线l,求l的方程;(2)、若函数在处取极小值,求a的取值范围.21. 已知椭圆:的左顶点为 , 圆:经过椭圆的上、下顶点.(1)、求椭圆的方程和焦距;(2)、已知 , 分别是椭圆和圆上的动点( , 不在坐标轴上),且直线与轴平行,线段的垂直平分线与轴交于点 , 圆在点处的切线与轴交于点.求线段长度的最小值.四、选做题