天津市南开区2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-07-28 类型：期末考试

进入出卷网下载

一、单选题

1. 已知图①～④，

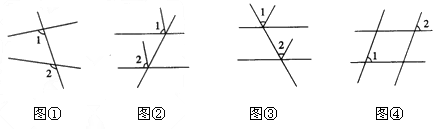
在上述四个图中，∠1与∠2是同位角的有（）

A、①②③④ B、①②③ C、①③ D、①

查看试题解析
2. 在实数 $- \frac{1}{3}$ ，－1，0， $\sqrt{3}$ 中，最小的实数是（　　）

A、－1 B、0 C、 $- \frac{1}{3}$ D、 $\sqrt{3}$

查看试题解析
3. 若点M在第四象限，且M到x轴的距离为1，到y轴的距离为2，则点M的坐标为（）

A、（1，－2） B、（2，1） C、（－2，1） D、（2，－1）

查看试题解析
4. 下列现象中，属于平移现象的是（）

A、方向盘的转动 B、行驶的自行车的车轮的运动 C、电梯的升降 D、钟摆的运动

查看试题解析
5. $\sqrt{9}$ 的算术平方根是（）

A、3 B、 $\sqrt{3}$ C、±3 D、± $\sqrt{3}$

查看试题解析
6. 点A（﹣3，5）关于x轴对称的点的坐标为（）

A、（﹣3，5） B、（3，﹣5） C、（﹣3，﹣5） D、（3，5）

查看试题解析
7. 如图，把一个长方形纸片沿 $E F$ 折叠后，点 $D$ 、 $C$ 分别落在 $D^{'}$ ， $C^{'}$ 的位置．若 $∠ E F B = 65 °$ ，则 $∠ A E D^{^{'}}$ 等于（）

A、25° B、40° C、50° D、65°

查看试题解析
8. 下列调查中，适宜采用全面调查方式的是（）

A、对全市每天丢弃的废旧电池数的调查 B、对冷饮市场上冰淇淋质量情况的调查 C、对全国中学生心理健康现状的调查 D、对我国首架大型民用直升机各零件部件的调查

查看试题解析
9. 已知2a^y＋⁵b^3x与b²^－^4ya^2x是同类项，那么x，y的值是（）．

A、 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = - 1 \end{array}$ C、 ${\begin{array}{l} x = 0 \\ y = - \frac{3}{5} \end{array}$ D、 ${\begin{array}{l} x = 7 \\ y = 0 \end{array}$

查看试题解析
10. 若M（ $x ， y$ ）满足 $2 x y = 1$ ，点M所在的象限是（）

A、第一、二象限 B、第一、三象限 C、第二、四象限 D、不能确定

查看试题解析
11. 若关于x的不等式组 ${\begin{array}{l} x < 2 \\ x > a - 1 \end{array}$ 有解，则a的取值范围是（）

A、 $a \leq 3$ B、 $a < 3$ C、 $a \geq 3$ D、 $a > 3$

查看试题解析
12. 正方形网格中的交点，我们称之为格点．如图所示的网格图中，每个小正方形的边长都为 $1$ ．现有格点 $A ， B$ ，那么，在网格图中找出格点 $C$ ，使以 $A ， B$ 和格点 $C$ 为顶点的三角形的面积为1．这样的 $C$ 点可找到的个数为（）

A、4 B、5 C、6 D、7

查看试题解析

二、填空题

13. 如图直线AB、CD、EF相交于点O，且AB⊥CD，∠1=40°，则∠2= ．

查看试题解析
14. 若点M（﹣2，7﹣a）是第二象限的点，则a的取值范围是．

查看试题解析
15. $2 a - 1$ 与 $4 + a$ 都是x的平方根，则 $x =$ ．

查看试题解析
16. 如图，在一块长为21m，宽为15m的长方形草地上，有一块弯曲的小路，小路的左边线向右平移1m就是它的右边线，则这块草地的绿地面积为m² ．

查看试题解析
17. 如果点 $A (m + 2 ， 2 m + 1)$ 在 $y$ 轴上，则 $m =$ ；

查看试题解析
18. 如图，在平面直角坐标系中， $A_{1} (1 ， 2)$ ， $A_{2} (2 ， 0)$ ， $A_{3} (3 ， - 2)$ ， $A_{4} (4 ， 0)$ ……根据这个规律，探究可得点 $A_{2022}$ 的坐标是．

查看试题解析

三、解答题

19. 为了丰富校园文化生活，某校计划在午间校园广播台播放“百家讲坛”的部分内容为了了解学生的喜好，抽取若干名学生进行问卷调查（每人只选一项内容），整理调查结果，绘制统计图如下：

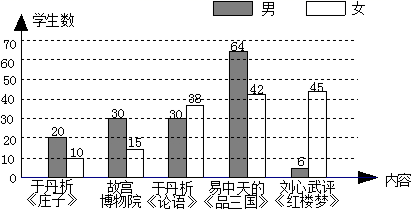
请根据统计图提供的信息回答以下问题：

(1)、这一调查属于（选填“抽样调查”或“普查”），抽取的学生数为名；

(2)、估计喜欢收听易中天《品三国》的学生约占全校学生的%（精确到小数点后一位）；

(3)、已知该校女学生共有1800名，则该校喜欢收听刘心武评《红楼梦》的女学生大约有多少名？

查看试题解析
20. 解方程组： ${\begin{array}{l} 4 x - y = 30 ① \\ x - 2 y = - 10 ② \end{array}$ ．

查看试题解析
21. 解不等式组： ${\begin{matrix} 3 (x ＋ 2) < x ＋ 8 \\ \frac{x}{2} \geq \frac{x - 1}{3} \end{matrix}$ ，并把它的解集在数轴上表示出来.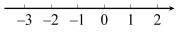

查看试题解析
22. 已知：如图，AE⊥BC，FG⊥BC，∠1＝∠2，∠D＝∠3+60°，∠CBD＝70°.

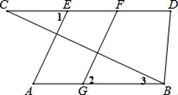(1)、求证：AB∥CD；

(2)、求∠C的度数.

查看试题解析
23. 某商店准备销售甲、乙两种商品共80件，已知甲商品进货价为每件70元，乙商品进货价为每件35元，在定价销售时，1件甲商品比1件乙商品售价多30元，3件甲商品比2件乙商品售价多150元．

(1)、每件甲商品与每件乙商品的售价分别是多少元？

(2)、若甲、乙两种商品的进货总投入不超过4200元，则至多进货甲商品多少件？

查看试题解析
24. 在平面直角坐标系中，点 $O$ 为坐标原点，正方形 $O A B C$ 与长方形 $D E F G$ 的位置如图所示，点 $A$ 在 $x$ 轴的正半轴上，点 $C$ 在 $y$ 轴的正半轴上，点 $B$ 的横坐标为 $a$ ，点 $D$ ， $E$ 在 $x$ 轴的负半轴上（点 $E$ 在点 $D$ 的右侧），点 $G$ 的坐标为 $（ b ， - b ）$ ， $D E = O A$ ，实数 $a$ ， $b$ 的值满足 $\sqrt{a - 4} + \sqrt{b + 6} = 0$ .

(1)、求点 $F$ 的坐标；

(2)、长方形 $D E F G$ 以每秒1个单位长度的速度向右平移 $t$ （ $t > 0$ ）秒得到矩形 $D' E' F' G'$ ，点 $D'$ ， $E'$ ， $F'$ ， $G'$ 分别为点 $D$ ， $E$ ， $F$ ， $G$ 平移后的对应点，设矩形 $D' E' F' G'$ 与正方形 $O A B C$ 重合部分的面积为 $S$ ，用含 $t$ 的式子表示 $S$ ，并直接写出相应的 $t$ 的范围；

(3)、在（2）的条件下，在长方形 $D E F G$ 出发运动的同时，点 $P$ 从点 $O$ 出发，沿正方形的边以每秒2个单位长度的速度顺时针方向运动（即 $O \to C \to B \to A \to O \to C$ ），连接 $P D'$ ， $P G'$ ，当三角形 $P D' G'$ 的面积为15时，求 $S > 0$ 时相应的 $t$ 值，并直接写出此时刻 $S$ 值及点 $P$ 的坐标．

查看试题解析