天津市滨海新区2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-07-28 类型：期末考试

进入出卷网下载

一、单选题

1. 9的平方根是（）

A、3 B、 $\pm 3$ C、 $- 3$ D、9

查看试题解析
2. 若点 $P (m ， 2 m - 4)$ 在y轴上，则点P的坐标是（）

A、 $(0 ， - 4)$ B、 $(0 ， 4)$ C、 $(- 2 ， 0)$ D、 $(2 ， 0)$

查看试题解析
3. 估计 $\sqrt{7}$ +1的值在（）

A、1到2之间 B、2到3之间 C、3到4之间 D、4到5之间

查看试题解析
4. 在实数 $\frac{11}{3} ， 0 ， \sqrt[3]{- 1} ， 3.1415926 ， \sqrt{16} ， 3 π$ 中，有理数的个数为（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
5. 下列说法正确的是（）

A、16的平方根是 $\sqrt{16}$ B、 $\sqrt{16} = 4$ C、 $\sqrt{16}$ =±4 D、以上都不对

查看试题解析
6. 如图，设点P是直线l外一点， $P Q ⊥ l$ ，垂足为点Q，点T是直线l上的一个动点，连接 $P T$ ，则（）

A、 $P T < P O$ B、 $P T > T Q$ C、 $P T ≥ P Q$ D、 $P T ≤ P Q$

查看试题解析
7. 下列图形中，由∠1=∠2能得到AB∥CD的是（）

A、 B、 C、 D、

查看试题解析
8. 下列调查中，最适合采用全面调查的是（）

A、了解我市中学生的消防安全意识 B、了解我市中学生每周体育锻炼的时间 C、了解某品牌新能源车的行驶里程 D、对我国首艘国产航母各种零部件质量情况的调查

查看试题解析
9. 若 $a > b$ ，则下列不等式一定成立的是：（）

A、 $a + 1 > b + 3$ B、 $a - 2 < b - 2$ C、 $\frac{a}{3} > \frac{b}{3}$ D、 $- a > - b$

查看试题解析
10. 下列说法错误的是（）

A、对顶角相等 B、两点之间，线段最短 C、同旁内角相等 D、若a∥b且b∥c，则a∥c

查看试题解析
11. 《九章算术》是中国古代第一部数学专著，它对我国古代后世的数学家产生了深远的影响.该书中记载了一个问题，大意是：有几个人一起去买一件物品，每人出8元，多3元；每人出7元，少4元.问有多少人?该物品价几何?设有x人.物品价值y元，则列方程组为（）

A、 ${\begin{array}{l} 8 x + 3 = x \\ 7 y - 4 = x \end{array}$ B、 ${\begin{array}{l} 8 x + 3 = y \\ 7 y - 4 = y \end{array}$ C、 ${\begin{array}{l} 8 y - 3 = x \\ 7 y + 4 = x \end{array}$ D、 ${\begin{array}{l} 8 x - 3 = y \\ 7 x + 4 = y \end{array}$

查看试题解析
12. 关于 $x$ 的不等式组 ${\begin{array}{l} 3 x - 1 > 4 (x - 1) \\ x < m \end{array}$ 的解集为 $x < 3$ ，那么 $m$ 的取值范围是（）

A、 $m \geq 3$ B、 $m > 3$ C、 $m < 3$ D、 $m = 3$

查看试题解析

二、填空题

13. $π - 3.14$ 的相反数是， $\sqrt[3]{- 64}$ 的绝对值是．

查看试题解析
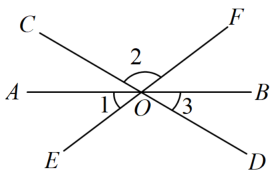
14. 如图，直线AB、CD、EF相交于点O，则∠1+∠2+∠3＝°．

查看试题解析
15. 一个容量为80的样本最大值是123，最小值是50，用频数分布直方图描述这一组数据，取组距为10，则可以分成组．

查看试题解析
16. 已知点M坐标为 $(2 - a ， 3 a + 6)$ 且M点到两坐标轴的距离相等，则点的M坐标是．

查看试题解析
17. 若关于x，y的方程组 ${\begin{array}{l} 2 x + y = k \\ x - 2 y = 3 \end{array}$ 的解x与y相等，则k的值为．

查看试题解析

三、解答题

18. 李强同学学完“相交线与平行线”一章后，在一本数学读物上看到一种只利用圆规和无刻度直尺作图的方法：
① 以∠AOB的顶点O为圆心，以适当长为半径画弧，交OA边于点M，交OB边于点N；② 作一条射线CD，以点C为圆心，以OM长为半径画弧，与射线CD交于点E；③ 以点E为圆心，以MN长为半径画弧，与②中所画弧交于点F；④ 过点F作射线CP，则∠PCD=∠BOA．如图1：
李强想利用这种方法过平面内一点Q作直线l的平行线a，如图2．

(1)、李强同学能借助上述方法作出直线l的平行线a吗？（填“能”或“不能”）.

(2)、如果能，请在图2中作出直线a，保留作图痕迹，并说明能够证明这两条直线平行的理由： ▲ ．

查看试题解析
19. 推理填空：完成下面的证明过程．
如图，AD $∥$ EF，∠1+∠2＝180°，DG⊥AC于点G，∠BAC＝90°．
求证：DG平分∠ADC．
证明：∵DG⊥AC（已知），
∴∠DGC＝90°（   ）．
∵∠BAC＝90°（已知），
∴∠DGC＝∠BAC，
∴  ▲   $∥$ AB（  ），
∴∠BAD＝∠ADG （   ）．
∵AD $∥$ EF（已知），
∴∠BAD+  ▲  ＝  ▲  （    ）．
∵∠1+∠2＝180°（已知），
∴∠BAD＝  ▲  （等量代换），
∴∠ADG＝  ▲  （等量代换），
∴DG平分∠ADC （    ）．

查看试题解析
20. 解方程组：

(1)、 ${\begin{array}{l} x - y = 13 \\ x = 6 y - 7 \end{array}$

(2)、 ${\begin{array}{l} \frac{1}{2} x - \frac{3}{2} y = - 3 \\ 2 x + 3 y = 3 \end{array}$

查看试题解析
21. 解不等式组 ${\begin{array}{l} 2 x - 1 > x + 1 ① \\ \frac{1}{2} x - 1 < 3 - \frac{3 x}{2} ② \end{array}$
请结合题意填空，完成本题的解答．

(1)、解不等式①，得；

(2)、解不等式②，得；

(3)、把不等式①和②的解集在数轴上表示出来：

(4)、原不等式组．

查看试题解析
22. 某同学在学习了数据的收集、整理与描述后，对其居住区域的部分居民随机进行了“手机品牌忠诚度”的问卷调查：A代表华为手机，B代表小米手机，C代表OPPO手机，D代表苹果手机，E代表VIVO手机，F代表其他品牌手机，并根据调查结果绘制成如图两幅不完整的统计图：
解答下列问题：

(1)、由图可知，有人参与了本次调查；

(2)、扇形统计图中，m的值是；

(3)、根据以上信息直接在答题卡中补全条形统计图；

(4)、根据以上调查结果，如果某同学所在的小区有6000人，请你估计该小区信赖华为手机的人数．

查看试题解析
23. 如图，点D是三角形ABC边CA延长线上一点，过点A作DC的垂线AP，MN是过点A的一条直线，且∠MAB=∠B，过点D作DE∥MN交AP于点E，求证：∠C+∠DEA=90°．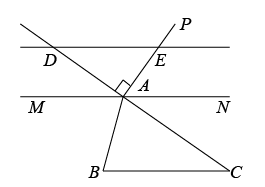

查看试题解析
24. 某地面对形势异常严峻的新冠疫情，遵从党和国家部署，最大程度保障人民群众的健康，将所在区域划分为封控区、管控区和防范区. 现要将一批蔬菜运往封控区，已知用3辆A型车和1辆B型车装满蔬菜一次可运26吨；用1辆A型车和2辆B型车装满蔬菜一次可运22吨．

(1)、求一辆A型车和一辆B型车装满蔬菜分别可运多少吨？

(2)、若一辆A型车的租金是180元，一辆B型车的租金是220元，该地计划租用A型车和B型车共7辆，且租金不超过1400元，问最多可租用几辆B型车？

查看试题解析
25. 如图，三角形AOB在平面直角坐标系中，A，B两点的坐标分别为（2 ， 4），（6 ， 2），O是坐标原点．

(1)、如图1，若把三角形AOB向左平移2个单位长度，然后再向上平移1个单位长度，顶点A、O、B的对应点分别是A′、O′、B′，则A′、O′、B′三个点的坐标分别是多少？

(2)、求三角形AOB的面积；

(3)、如图2，x轴上一动点P，从点（－3 ， 0）运动到点（2 ， 0），连接PA和PB，求三角形APB面积的取值范围．

查看试题解析