山西省太原市2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-07-28 类型：期末考试

进入出卷网下载

一、单选题

1. 计算 $2^{- 1}$ 的结果是（　　）．

A、﹣ $\frac{1}{2}$ B、 $\frac{1}{2}$ C、2 D、﹣2

查看试题解析
2. 面对新冠疫情，我国毫不动摇坚持动态清零总方针，外防输入，内防反弹．下面是支付宝“国家政务服务平台”上与疫情防控相关的四个小程序图标，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 劳动课上，小莉要用三根木棒首尾相接钉一个三角形框架，现有两根木棒长分别为4cm，5cm，则第三根木棒的长可取（）

A、1cm B、4cm C、9cm D、10cm

查看试题解析
4. 如图的三张卡片除正面图案外完全相同，分别印有杭州2022年第19届亚运会的吉祥物—宸宸、琮琮和莲莲．现将三张卡片背面朝上放置，打乱后随机抽取一张，恰好抽到“莲莲”的概率是（）

A、1 B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、 $\frac{1}{3}$

查看试题解析
5. 如图，已知a∥c，添加下列条件后，能推出b∥c的是（）

A、∠5＋∠2＝180° B、∠3＝∠6 C、∠4＋∠6＝180° D、∠1＝∠2

查看试题解析
6. 下列运算正确的是（）

A、a⁴·a²＝a⁸ B、a⁶÷a²＝a³ C、（a＋3）（a－3）＝a²－6 D、（－a²）³＝－a⁶

查看试题解析
7. 如图是苏阿姨手机上显示的太原市某日空气质量情况，其中PM2.5值为24微克/m，即0.000024克/m．数据0.000024用科学记数法表示为（）

A、2.4×10⁵ B、24×10^－4 C、2.4×10^－5 D、0.24×10^－6

查看试题解析
8. 下列随机试验中，结果具有“等可能性”的是（）

A、掷一枚质地均匀的骰子 B、篮球运动员定点投篮 C、掷一个矿泉水瓶盖 D、从装有若干小球的透明袋子摸球

查看试题解析
9. 骑行是一种健康自然的运动旅游方式，长期坚持骑自行车可增强心血管功能，提高人体新陈代谢和免疫力．如图是骑行爱好者小李某日骑自行车行驶路程（km）与时间（h）的图象，观察图象得到下列信息，其中正确的是（）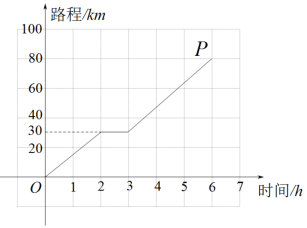

A、小李实际骑行时间为6h B、点P表示出发6h，小李共骑行80km C、3－6h小李的骑行速度比0－2h慢 D、3h内，小李的平均速度是15km/h

查看试题解析
10. 如图，在△ABC中，AB＝AC，按如下步骤作图：以点A为圆心、适当长度为半径作弧，分别交AB、AC于点M、N；分别以点M、N为圆心、大于 $\frac{1}{2}$ MN的长为半径作弧，两弧相交于点F，连接AF并延长，交BC于点E．下列结论不一定成立的是（）

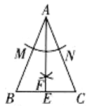A、∠ABC＝∠ACB B、BE＝CE C、AE⊥BC D、∠BAE＝ $\frac{1}{2}$ ∠B

查看试题解析

二、填空题

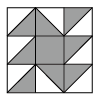
11. 小球在如图所示的地板上自由地滚动，并最终随机地停留在某块方砖上（每块方砖除颜色外完全相同），则小球停留在黑色区域的概率是．

查看试题解析
12. 一个等腰三角形的底角是顶角的2倍，则顶角的大小是．

查看试题解析
13. 如图，点D、E分别在线段AB、AC上，AE=AD，要使△ABE≌△ACD，则需添加的一个条件是.

查看试题解析
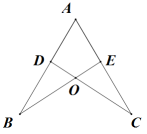14. 2022年5月15日，由中科院自主研发的“极目一号”型浮空艇，在海拔4270米的中科院珠峰站附近发放场地升空，创造了海拔9032米的大气科学观测世界纪录．下表表示某日珠峰附近一测量点海拔高度h（米）与相应高度处气温t（℃）的关系，根据表格数据，当时该测量点海拔8270米处的气温是 ℃．
海拔高度h/米
4270
5270
6270
7270
…
气温t/℃
-15
-21
-27
-33
…

查看试题解析
15. 如图，在三角形纸片ABC中，∠ACB＝90°，∠A＝40°，点D在AB边上（不与A、B重合），连接CD，将△ACD沿CD所在直线折叠得到△A′CD，A′C交AB于点E．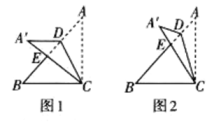
请从A、B两题中任选一题作答．我选择题．
A．如图1，若A′D∥BC，则∠ACD的度数为．
B．如图2，若A′E＝A′D，则∠ACD的度数为．

查看试题解析

三、解答题

16.

(1)、计算： ①2x³y·（－ $\frac{1}{2}$ xy²）²；
②（x＋2y）（x－2y ）＋3y²；

(2)、先化简，再求值：[（4a＋b）（b－a）＋（2a－b）²]÷（－b），其中 a＝－2，b＝1．

查看试题解析
17. 为纪念中国共青团成立100周年，校团委举办“走进百年团史，追寻信仰之光”知识竞赛，并设立了一个可以自由转动的转盘（如图所示），每位参赛同学都有一次转动转盘的机会．已知该转盘被等分成16个扇形，当转盘停止后，若指针正好对准红色、黄色、绿色区域，就可以分别获得笔记本、签字笔或书签作纪念品．小华参加知识竞赛后，转动一次转盘，他获得纪念品的概率是多少？

查看试题解析
18. 已知：如图，△ABC．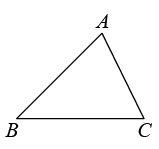

(1)、求作：△DEF，使△DEF≌△ABC（要求：在指定区域尺规作图，不写作法，保留作图痕迹）；

(2)、根据作图过程写出△DEF≌△ABC的依据：．

查看试题解析

19. 数学课上，同学们通过撕、拼的方法，探索、验证三角形的内角和等于180°．下面是小彬的课堂笔记，请阅读操作方法，补全说理过程．

如图1，△ABC中的三个内角分别为∠1，∠2，∠3．将∠2和∠3撕下，按图2的方式拼摆，使∠2和∠3的顶点均与∠1的顶点重合，∠2的一边与AB重合，∠3的一边与AC重合．

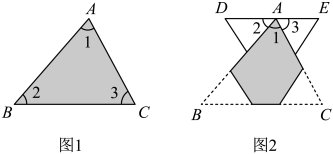
理由：由操作可知∠B＝∠2，

所以AD∥ ▲ （依据： ▲ ）．

同理，∠C＝∠3，

所以， ▲ ∥ ▲ ，

所以，AD、AE在同一直线上，

所以，∠DAE＝ ▲ ° ，

即 ∠1＋ ▲ ＋ ▲ ＝ ▲ ．

查看试题解析

20. 近视眼镜是一种为了矫正视力，让人们可以清晰看到远距离物体的眼镜．近视眼镜的镜片是凹透镜，研究发现，近视眼镜的度数y（度）与镜片焦距x（m）的关系式为y＝ $\frac{100}{x}$ ．

(1)、上述问题中，当x的值增大，y的值随之（填“增大”“减小”或“不变”）；

(2)、根据y与x的关系式补全下表：
焦距x/m
0.1
0.2
……
度数y/度
1000
400
……

(3)、小明原来佩戴400度近视眼镜，经过一段时间的矫正治疗加之注意用眼健康，复查验光时，所配镜片焦距调整为0.4m，则小明的眼镜度数下降了多少度？

查看试题解析
21. 如图，点E、C在线段BF上，点A、D在BF同侧，AC、DE相交于点O．若OE＝OC，BE＝CF，∠B＝∠F，则∠A与∠D相等吗？说明理由．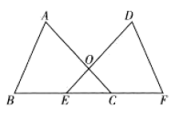

查看试题解析

22. 阅读下面材料，完成相应的任务：

阿贝尔公式

数学界三大奖项之一的阿贝尔奖，是为了纪念挪威著名数学家阿贝尔所设．阿贝尔是近代数学发展的先驱，他年轻时利用阶梯图形，发现了重要的恒等式——阿贝尔公式．

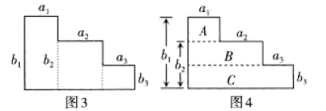
如右图，用两种方法将一个二级阶梯图形分别分割成两个长方形．按图1的方法，该阶梯图形的面积为 $a_{1} b_{1} + a_{2} b_{2}$ ；按图2的方法，长方形①的面积为 $a_{1} (b_{1} - b_{2})$ ，长方形②的面积为 $(a_{1} + a_{2}) b_{2}$ ，根据图1、图2面积相等，可得到二级阶梯图形对应的阿贝尔公式： $a_{1} b_{1} + a_{2} b_{2} = a_{1} (b_{1} - b_{2}) + (a_{1} + a_{2}) b_{2}$ ．

任务：

(1)、推理验证：材料中的阿贝尔公式可用代数运算验证，请补全如下说理过程：

因为右边＝．

左边＝a₁b₁＋a₂b₂ ，左边＝右边，

所以，a₁b₁＋a₂b₂＝a₁（b₁－b₂）＋（a₁＋a₂）b₂ ．

(2)、类比探究：如下图，用两种方法将一个三级阶梯图形分别分割成三个长方形．

①图4中长方形B的长为a₁＋a₂ ，宽为 ▲ ；

②由图3、图4面积相等，可得三级阶梯图形对应的阿贝尔公式为：a₁b₁＋a₂b₂＋a₃b₃＝a_l（b_l－b₂）＋ ▲ ＋ ▲ ．

请补全该公式，并进行验证．

查看试题解析

23. 综合与实践
问题情境：数学课上，同学们以等腰直角三角形为背景，探究线段之间的数量关系．
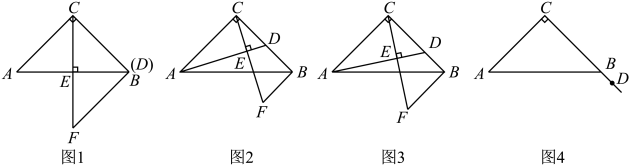
已知：在Rt△ABC中，AC＝BC，∠ACB＝90°，D是射线CB上的一个动点，连接AD，过点C作AD的垂线，垂足为点E，过点B作AC的平行线交CE的延长线于点F．
独立思考：

(1)、如图1，当点D与点B重合时，小颖发现BF＝AC，请你帮她说明理由；

(2)、如图2，当点D为BC中点时，直接写出线段BF与AC的数量关系；
合作交流：

(3)、①如图3，当点D在线段CB上（不与C、B重合），请探究线段BF、BD与AC之间的数量关系（要求：写出发现的结论，并说明理由）．
②如图4，当点D在线段CB延长线上，请探究线段BF、BD与AC之间的数量关系（要求：画出图形，写出发现的结论，并说明理由）．

查看试题解析

海拔高度h/米	4270	5270	6270	7270	…
气温t/℃	-15	-21	-27	-33	…

焦距x/m	0.1	0.2		……
度数y/度	1000		400	……