山西省晋中市2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-07-28 类型:期末考试
一、单选题
-
1. 计算的正确结果是( )A、m B、 C、 D、2. 随着现代室内设计的不断发展,具有个性和时代感的设计风格在当今时代被人们所追捧,多数设计风格植入了山西大院窗格的图案、纹样等元素,以下是部分窗格的设计图案,其中不属于轴对称图形的是( )A、
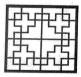 B、
B、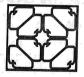 C、
C、 D、
D、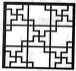 3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,用三角尺经过直线l外一点A画这条直线的垂线,这样的垂线我们只能画出一条.这里面蕴含的数学原理是( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,用三角尺经过直线l外一点A画这条直线的垂线,这样的垂线我们只能画出一条.这里面蕴含的数学原理是( )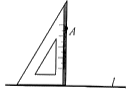 A、垂线段最短 B、两点之间线段最短 C、平面内,过一点有且只有一条直线与已知直线垂直 D、过直线外一点有且只有一条直线与这条直线平行5. 用三根长度分别为3cm,5cm,10cm的木条首尾顺次相接围成一个三角形,这属于下列事件中的( )A、不可能事件 B、随机事件 C、必然事件 D、不确定事件6. 如图1,边长为a的大正方形中有一个边长为b的小正方形.将图1中的阴影部分拼成了一个长方形(如图2),根据两个图形中阴影部分的面积相等,可以验证平方差公式 , 这种验证方法体现的数学思想是( )
A、垂线段最短 B、两点之间线段最短 C、平面内,过一点有且只有一条直线与已知直线垂直 D、过直线外一点有且只有一条直线与这条直线平行5. 用三根长度分别为3cm,5cm,10cm的木条首尾顺次相接围成一个三角形,这属于下列事件中的( )A、不可能事件 B、随机事件 C、必然事件 D、不确定事件6. 如图1,边长为a的大正方形中有一个边长为b的小正方形.将图1中的阴影部分拼成了一个长方形(如图2),根据两个图形中阴影部分的面积相等,可以验证平方差公式 , 这种验证方法体现的数学思想是( )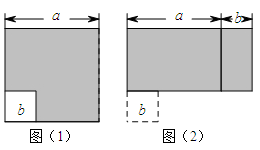 A、数形结合思想 B、方程思想 C、统计思想 D、分类思想7. 今年4月我国首个海洋领域的冷冻电镜中心建成并对外开放共享,冷冻电镜是一种能够对生物样品实现高分辨三维结构解析的高精尖设备,其观测水平达到0.1纳米级别,即0.0000000001米.数据0.0000000001米用科学记数法表示为( )
A、数形结合思想 B、方程思想 C、统计思想 D、分类思想7. 今年4月我国首个海洋领域的冷冻电镜中心建成并对外开放共享,冷冻电镜是一种能够对生物样品实现高分辨三维结构解析的高精尖设备,其观测水平达到0.1纳米级别,即0.0000000001米.数据0.0000000001米用科学记数法表示为( ) A、米 B、米 C、米 D、米8. 端午节吃粽子是中华民族的传统习俗.端午节这天小颖的妈妈买了2只红豆粽和4只红枣粽,这些粽子除了内部馅料不同外其他均相同.小颖从中随意选一个,她选到红豆粽的概率是( )
A、米 B、米 C、米 D、米8. 端午节吃粽子是中华民族的传统习俗.端午节这天小颖的妈妈买了2只红豆粽和4只红枣粽,这些粽子除了内部馅料不同外其他均相同.小颖从中随意选一个,她选到红豆粽的概率是( ) A、 B、 C、 D、19. 用一块含60°角的直角三角板和一把直尺按图中所示的方式放置,其中直尺的直角顶点与三角板的60°角顶点重合,直尺两边分别与三角板的两条直角边相交,若 , 则的度数为( )
A、 B、 C、 D、19. 用一块含60°角的直角三角板和一把直尺按图中所示的方式放置,其中直尺的直角顶点与三角板的60°角顶点重合,直尺两边分别与三角板的两条直角边相交,若 , 则的度数为( ) A、25° B、22.5° C、20° D、15°10. 某生物实验小组研究发现,某种种子发芽率与浸泡时间有下面关系,下列说法正确的是( )
A、25° B、22.5° C、20° D、15°10. 某生物实验小组研究发现,某种种子发芽率与浸泡时间有下面关系,下列说法正确的是( )浸泡时间/时
0
2
6
8
10
12
14
16
20
发芽率/%
15.9
26.1
32.3
35
53
61
43.1
10.8
30.5
A、种子发芽率为自变量,种子浸泡时间为因变量 B、随着种子浸泡时间的加大,种子发芽率在提高 C、随着种子浸泡时间的加大,种子发芽率在降低 D、由表格可以看出,种子浸泡时间为12小时左右比较适宜二、填空题
-
11. 计算: .12. 下表记录了一名球员在罚球线上投篮的结果,估计这名球员在罚球线投篮,一次投中的概率为 . (精确到0.01)
投篮次数
100
200
300
500
1000
1500
投中次数
58
130
189
324
651
978
投中频率
0.580
0.650
0.630
0.648
0.654
0.652
13. 小红用一根长为60cm的铁丝围成一个长方形,若一边长为 , 相邻的另一边长为 , 则与的关系为 .14. 如图,已知 , , 请添加一个你认为适合的条件,使 . 你添加的条件是 .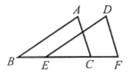 15. 如图,△ABC中, , 边AB的垂直平分线分别交AC,AB于点D,E,连接BD,若 , 则度.
15. 如图,△ABC中, , 边AB的垂直平分线分别交AC,AB于点D,E,连接BD,若 , 则度.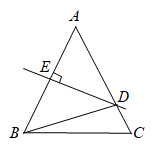
三、解答题
-
16. 计算:(1)、;(2)、 .17. 先化简,再求值: , 其中 .18. 请在网格中完成下列问题:
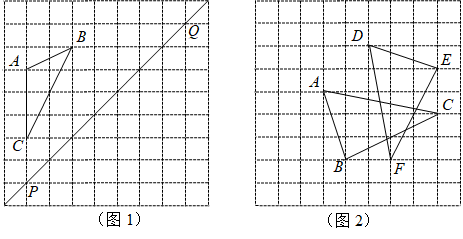 (1)、在图1中画出△ABC关于直线PQ成轴对称的;(2)、在图2中画出△ABC与△DEF的对称轴.19. 某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被分成若干扇形区域)进行抽奖促销活动,并规定:凡在商场消费的顾客,均可获得一次转动转盘的机会.如果转盘停止后,指针所指区域为“一等奖”、“二等奖”、“三等奖”、“四等奖”、“五等奖”,则可获得对应的奖品;指针所指区域为“谢谢”则没有奖品;指针指向两区域的边界线,顾客可以再转动一次,直到指针不指向边界线时停止.根据以上规则,回答下列问题:
(1)、在图1中画出△ABC关于直线PQ成轴对称的;(2)、在图2中画出△ABC与△DEF的对称轴.19. 某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被分成若干扇形区域)进行抽奖促销活动,并规定:凡在商场消费的顾客,均可获得一次转动转盘的机会.如果转盘停止后,指针所指区域为“一等奖”、“二等奖”、“三等奖”、“四等奖”、“五等奖”,则可获得对应的奖品;指针所指区域为“谢谢”则没有奖品;指针指向两区域的边界线,顾客可以再转动一次,直到指针不指向边界线时停止.根据以上规则,回答下列问题: (1)、若“三等奖”所在扇形的圆心角为50°,则顾客获得三等奖的概率为;(2)、若商场计划让顾客通过转动一次转盘获得“五等奖”的概率为 , 请你求出转盘中“五等奖”所在扇形的圆心角度数.20. 如图, , , 若 , 试求的度数.请补充求解过程,并在括号内填上相应的理由.
(1)、若“三等奖”所在扇形的圆心角为50°,则顾客获得三等奖的概率为;(2)、若商场计划让顾客通过转动一次转盘获得“五等奖”的概率为 , 请你求出转盘中“五等奖”所在扇形的圆心角度数.20. 如图, , , 若 , 试求的度数.请补充求解过程,并在括号内填上相应的理由.解:因为 , 所以 .
又因为 ,
所以∠ ▲ =∠ ▲ .
所以( ).
所以 ▲ ( ).
又因为 , 所以 ▲ .
 21. 小明听到弟弟诵读诗句“儿童散学归来早,忙趁东风放纸鸢”时,他想借助图象大致刻画出诗句中儿童从学校放学回家,再到田野这段时间内,离家距离的变化情况.(1)、下列图象中能大致刻画这段时间儿童离家距离与时间关系的是( );A、
21. 小明听到弟弟诵读诗句“儿童散学归来早,忙趁东风放纸鸢”时,他想借助图象大致刻画出诗句中儿童从学校放学回家,再到田野这段时间内,离家距离的变化情况.(1)、下列图象中能大致刻画这段时间儿童离家距离与时间关系的是( );A、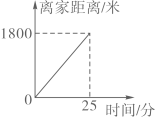 B、
B、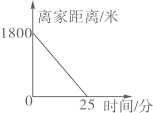 C、
C、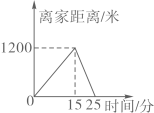 D、
D、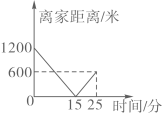 (2)、根据符合题意图象中的相关数据可知儿童家到学校的距离是米,儿童从家出发到田野所用时间为分;(3)、小明想自己动手制作风筝和弟弟一起去放,他画出了如下风筝示意图,其中 , , 他认为根据示意图,不用测量就能知道 . 你同意他的观点吗?请说明理由.
(2)、根据符合题意图象中的相关数据可知儿童家到学校的距离是米,儿童从家出发到田野所用时间为分;(3)、小明想自己动手制作风筝和弟弟一起去放,他画出了如下风筝示意图,其中 , , 他认为根据示意图,不用测量就能知道 . 你同意他的观点吗?请说明理由.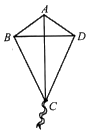 22. 请仔细阅读以下材料,并按要求完成相应任务.
22. 请仔细阅读以下材料,并按要求完成相应任务.问题情景:数学课上,老师让同学们利用尺规作的平分线(如图1).
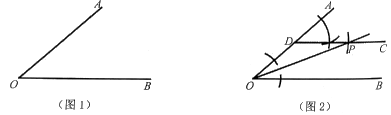
下面是小亮同学的作法(如图2):
①在射线OA上取一点D(不同于点O),作 , 使点C落在内部;
②以点D为圆心,以DO长为半径作弧,交射线DC于点P;
③作射线OP.
射线OP就是的平分线.
展示交流:
小亮同学对自己作法的符合题意性做了如下说明:
由作图步骤①可知 , 所以(依据1).所以 .
由作图步骤②可知 , 所以(依据2).所以 .
所以射线OP是的平分线.
问题解决:
(1)、写出上述小亮同学说明过程中依据1,依据2的具体内容:依据1:
依据2:
(2)、请你用不同于小亮的方法,利用尺规在图1完成老师的任务.(要求:保留作图痕迹,不写作法)23. 在一次数学活动课上,刘老师准备了两个等腰三角形,如图1,△ABC和△DEF中, , , 且 , 让同学们通过不同的摆放方式探究一些线段或角的关系.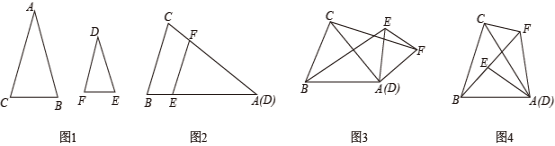 (1)、如图2,“冲锋小组”的同学将△ABC和△DEF的顶角顶点重合,且DE和DF分别落在边AB,AC上,请直接写出此时线段BE和CF的数量关系:;(2)、如图3,“智慧小组”的同学将△ABC和△DEF的顶角顶点重合,但DE未落在边AB上,连接BE,CF.此时(1)中的结论还成立吗?并说明理由;(3)、如图4,“创新小组”的同学将△ABC和△DEF的顶角顶点重合,且点B,E,F在同一条直线上,若 , , 请直接写出的度数.
(1)、如图2,“冲锋小组”的同学将△ABC和△DEF的顶角顶点重合,且DE和DF分别落在边AB,AC上,请直接写出此时线段BE和CF的数量关系:;(2)、如图3,“智慧小组”的同学将△ABC和△DEF的顶角顶点重合,但DE未落在边AB上,连接BE,CF.此时(1)中的结论还成立吗?并说明理由;(3)、如图4,“创新小组”的同学将△ABC和△DEF的顶角顶点重合,且点B,E,F在同一条直线上,若 , , 请直接写出的度数.