山东省济南市高新区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-07-28 类型:期末考试
一、单选题
-
1. 北京2022年冬奥会会徽(冬梦),是第24届冬季奥林匹克运动会使用的标志,主要由会徽图形、文字标志、奥林匹克五环标志组成,组成会徽的四个图案中是轴对称图形的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 如图,把两根木条AB和AC的一端A用螺栓固定在一起,木条AB自由转动至AB′位置.在转动过程中,下面的量是常量的为( )
2. 如图,把两根木条AB和AC的一端A用螺栓固定在一起,木条AB自由转动至AB′位置.在转动过程中,下面的量是常量的为( ) A、∠BAC的度数 B、AB的长度 C、BC的长度 D、△ABC的面积3. 下列各组数中不可能是一个三角形的边长的是( )A、3,4,5 B、5,7,7 C、5,7,12 D、6,8,104. 下列事件中,确定事件是( )A、打开电视机,正在播放广告 B、买一张电影票,座位号是奇数号 C、3天内会下雨 D、13个人中至少有2人生日在同一个月5. 一个大正方形,被两条线段分割成两个小正方形和两个小长方形,若两个小正方形的面积分别为10和6,则小长方形的对角线AB的长为( )
A、∠BAC的度数 B、AB的长度 C、BC的长度 D、△ABC的面积3. 下列各组数中不可能是一个三角形的边长的是( )A、3,4,5 B、5,7,7 C、5,7,12 D、6,8,104. 下列事件中,确定事件是( )A、打开电视机,正在播放广告 B、买一张电影票,座位号是奇数号 C、3天内会下雨 D、13个人中至少有2人生日在同一个月5. 一个大正方形,被两条线段分割成两个小正方形和两个小长方形,若两个小正方形的面积分别为10和6,则小长方形的对角线AB的长为( )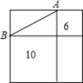 A、4 B、6 C、10 D、166. 计算(﹣x2)•(﹣x3)4的结果为( )A、﹣x9 B、x9 C、﹣x14 D、x147. 下列图形中,线段PQ的长表示点P到直线MN的距离是( )A、
A、4 B、6 C、10 D、166. 计算(﹣x2)•(﹣x3)4的结果为( )A、﹣x9 B、x9 C、﹣x14 D、x147. 下列图形中,线段PQ的长表示点P到直线MN的距离是( )A、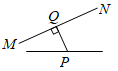 B、
B、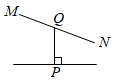 C、
C、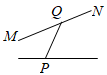 D、
D、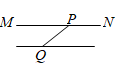 8. 观察下面图形,从图1到图2可用式子表示为( )
8. 观察下面图形,从图1到图2可用式子表示为( )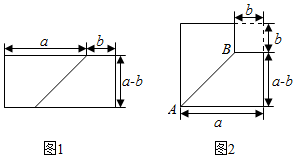 A、(a+b)(a﹣b)=a2﹣b2 B、a2﹣b2=(a+b)(a﹣b) C、(a+b)2=a2+2ab+b2 D、a2+2ab+b2=(a+b)29. 如图,欣欣妈妈在超市购买某种水果所付金额y(元)与购买x(千克)之间的关系如图所示,则“一次性购买6千克这种水果”比“分2次每次购买3千克这种水果”可节省( )元.
A、(a+b)(a﹣b)=a2﹣b2 B、a2﹣b2=(a+b)(a﹣b) C、(a+b)2=a2+2ab+b2 D、a2+2ab+b2=(a+b)29. 如图,欣欣妈妈在超市购买某种水果所付金额y(元)与购买x(千克)之间的关系如图所示,则“一次性购买6千克这种水果”比“分2次每次购买3千克这种水果”可节省( )元. A、4 B、3 C、2 D、110. 如图,DE,DF分别是线段AB,BC的垂直平分线,连接DA,DC,则( )
A、4 B、3 C、2 D、110. 如图,DE,DF分别是线段AB,BC的垂直平分线,连接DA,DC,则( )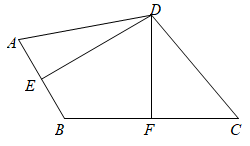 A、∠A=∠C B、∠B=∠ADC C、DA=DC D、DE=DF11. 如图,要判断一块纸带的两边a,b相互平行,甲、乙、丙三人的折叠与测量方案如下:
A、∠A=∠C B、∠B=∠ADC C、DA=DC D、DE=DF11. 如图,要判断一块纸带的两边a,b相互平行,甲、乙、丙三人的折叠与测量方案如下: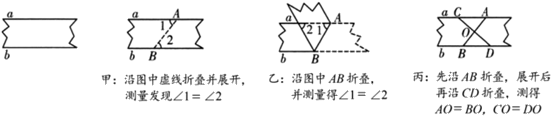
下列判断正确的是( )
A、甲、乙能得到 , 丙不能 B、甲、丙能得到 , 乙不能 C、乙、丙能得到 , 甲不能 D、甲、乙、丙均能得到12. 在我国古代数学著作《九章算术》“勾股”章中有一题:“今有开门去阃(kǔn)一尺,不合二寸,问门广几何?”大意是说:如图,推开双门(AD和BC),门边缘D、C两点到门槛AB的距离为1尺(1尺=10寸),双门间的缝隙CD为2寸,那么门的宽度(两扇门的和)AB为( )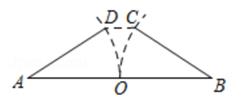 A、103寸 B、102寸 C、101寸 D、100寸
A、103寸 B、102寸 C、101寸 D、100寸二、填空题
-
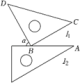
13. 计算: .14. 将一副三角尺按如图的方式摆放,其中l1∥l2 , 则∠α的度数是 °.
 15. 我国首辆火星车正式被命名为“祝融”,为应对极限温度环境,火星车使用的是新型隔温材料——纳米气凝胶,该材料导热率与温度T(℃)的关系如下表:
15. 我国首辆火星车正式被命名为“祝融”,为应对极限温度环境,火星车使用的是新型隔温材料——纳米气凝胶,该材料导热率与温度T(℃)的关系如下表:温度T(℃)
100
150
200
250
300
350
400
导热率K
0.15
0.2
0.25
0.3
0.35
0.4
0.45
根据表格中两者的对应关系,若导热率为 , 则温度为℃.
16. 已知:如图, ,只需补充条件 , 就可以根据“ ”得到 . 17. 用四个全等的直角三角形拼成如图一个大正方形ABCD和一个小正方形EFGH,这就是著名的“赵爽弦图”,若AB=15,AF=12,则小正方形EFGH的面积为
17. 用四个全等的直角三角形拼成如图一个大正方形ABCD和一个小正方形EFGH,这就是著名的“赵爽弦图”,若AB=15,AF=12,则小正方形EFGH的面积为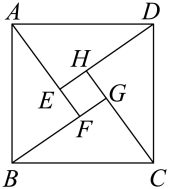 18. 如图,等腰△ABC中,AB=AC,∠BAC=45°,AD⊥BC于D.过C作CE⊥AB于E,交AD于H,EF⊥AC于F,交AD于G,连接BH.下列结论:①S△AEH:S△ACH=AE:AC;②EG∥BH;③AH=2CH;④AD=EF;⑤AC=CE+GE.其中正确的是 .
18. 如图,等腰△ABC中,AB=AC,∠BAC=45°,AD⊥BC于D.过C作CE⊥AB于E,交AD于H,EF⊥AC于F,交AD于G,连接BH.下列结论:①S△AEH:S△ACH=AE:AC;②EG∥BH;③AH=2CH;④AD=EF;⑤AC=CE+GE.其中正确的是 .
三、解答题
-
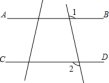
19. 计算:(3m﹣1)(m+5).20. 已知am=2,an=3,求a2m+3n的值.21. 如图,如果∠1=∠2,那么AB∥CD吗?说出你的理由.
 22. 下面的图象记录了某地1月份某天的温度随时间变化的情况,请你仔细观察图象后回答下面的问题.
22. 下面的图象记录了某地1月份某天的温度随时间变化的情况,请你仔细观察图象后回答下面的问题.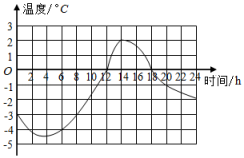 (1)、20时的温度是℃,最暖和的时刻是时,温度是0℃的时刻是时,温度在﹣3℃以下的持续时间为h.(2)、你从图象中还能获取哪些信息(写出1条即可).23. 如图,点E,F在线段AD上,AB∥CD, , . 求证: .
(1)、20时的温度是℃,最暖和的时刻是时,温度是0℃的时刻是时,温度在﹣3℃以下的持续时间为h.(2)、你从图象中还能获取哪些信息(写出1条即可).23. 如图,点E,F在线段AD上,AB∥CD, , . 求证: .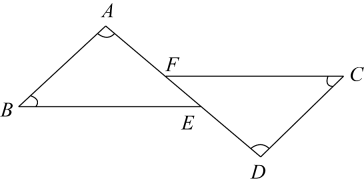 24. 先化简,再求值:(x﹣2y)2﹣(x+y)(x﹣y),其中 , y=1.25. 如图,在△ABC中,∠ACB=90°,AC=20,BC=15,CD⊥AB于点D.求:CD的长.
24. 先化简,再求值:(x﹣2y)2﹣(x+y)(x﹣y),其中 , y=1.25. 如图,在△ABC中,∠ACB=90°,AC=20,BC=15,CD⊥AB于点D.求:CD的长.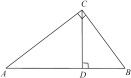 26. 暑假降至,丹尼斯大卖场为回馈新老顾客,进行有奖促销活动活动. 活动规定:购买500元的商品就可以获得一次转转盘的机会(转盘分为5个区域,分别是特等奖、一等奖、二等奖、三等奖、不获奖),转盘指针停在哪个获奖区域就可以得到该区域相应等级奖品一件(如果指针恰好停在分割线上,那么重转一次,直到指针指向某一区域为止). 大卖场工作人员在制作转盘时,将各扇形区域圆心角(不完全)分配如下表:
26. 暑假降至,丹尼斯大卖场为回馈新老顾客,进行有奖促销活动活动. 活动规定:购买500元的商品就可以获得一次转转盘的机会(转盘分为5个区域,分别是特等奖、一等奖、二等奖、三等奖、不获奖),转盘指针停在哪个获奖区域就可以得到该区域相应等级奖品一件(如果指针恰好停在分割线上,那么重转一次,直到指针指向某一区域为止). 大卖场工作人员在制作转盘时,将各扇形区域圆心角(不完全)分配如下表:奖次
特等奖
一等奖
二等奖
三等奖
不获奖
圆心角
促销公告:凡购买我大卖场商品500元均有可能获得下列奖品:
特等奖:山地越野自行车一辆 一等奖:双肩背包一个
二等奖:洗衣液一桶 三等奖:抽纸一盒
根据以上信息,解答下列问题:
(1)、求不获奖的扇形区域圆心角度数是多少?(2)、求获得双肩背包的概率是多少?(3)、甲顾客购物520元,求他获奖的概率是多少?27. 如图1,已知△ABC中,BC=6,AF为BC边上的高,P是BC上一动点,沿BC由B向C运动,连接AP,在这个变化过程中设BP=x,且把x看成自变量,设△APC的面积为S,图2刻画的是S随x变化而变化的图象,根据图象回答以下问题: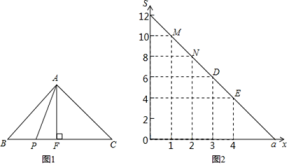 (1)、△ABC的高AF的长为 .(2)、写出S与x的关系式 .(3)、设△ABP的面积为y,写出y与x的关系式,并求当x为何值时,△APC的面积与△ABP的面积相等?28. 如图,在△ABC中,AB=AC,作AB边的垂直平分线交直线BC于M,交AB于点N.
(1)、△ABC的高AF的长为 .(2)、写出S与x的关系式 .(3)、设△ABP的面积为y,写出y与x的关系式,并求当x为何值时,△APC的面积与△ABP的面积相等?28. 如图,在△ABC中,AB=AC,作AB边的垂直平分线交直线BC于M,交AB于点N. (1)、如图(1),若∠A=40°,则∠NMB=度;(2)、如图(2),若∠A=70°,则∠NMB=度;(3)、如图(3),若∠A=120°,则∠NMB= 度;(4)、由(1)(2)(3)问,你能发现∠NMB与∠A有什么关系?写出猜想,并证明.29. 问题发现:若x满足(9﹣x)(x﹣4)=2,求(9﹣x)2+(x﹣4)2的值.
(1)、如图(1),若∠A=40°,则∠NMB=度;(2)、如图(2),若∠A=70°,则∠NMB=度;(3)、如图(3),若∠A=120°,则∠NMB= 度;(4)、由(1)(2)(3)问,你能发现∠NMB与∠A有什么关系?写出猜想,并证明.29. 问题发现:若x满足(9﹣x)(x﹣4)=2,求(9﹣x)2+(x﹣4)2的值.小明在解决该问题时,采用了以下解法:
解:设(9﹣x)=a,(x﹣4)=b,
则ab=(9﹣x)(x﹣4)= ▲ , a+b=(9﹣x)+(x﹣4)= ▲ .
所以(9﹣x)2+(x﹣4)2=a2+b2=(a+b)2﹣2ab= ▲ .
(1)、请补全小明的解法;(2)、已知(30﹣x)(x﹣20)=﹣10,则(30﹣x)2+(x﹣20)2的值为 .(3)、若x满足(2023﹣x)2+(x﹣2021)2=2022,求(2023﹣x)(x﹣2021)的值.(4)、如图,正方形ABCD的边长为x,AE=1,CG=3,长方形EFGD的面积是10,分别以DE、DG为边长作正方形MEDQ和NGDH,PQDH是长方形,求图中阴影部分的面积为(结果必须是一个具体数值).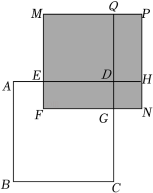 30. 如图1,△ABE是等腰三角形,AB=AE,∠BAE=45°,过点B作BC⊥AE于点C,在BC上截取CD=CE,连接AD、DE并延长AD交BE于点P;
30. 如图1,△ABE是等腰三角形,AB=AE,∠BAE=45°,过点B作BC⊥AE于点C,在BC上截取CD=CE,连接AD、DE并延长AD交BE于点P;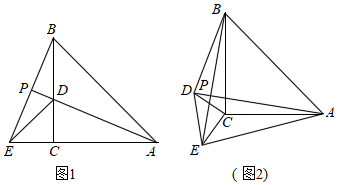 (1)、求证:AD=BE;(2)、试说明AD平分∠BAE.(3)、如图2,将△CDE绕着点C旋转一定的角度,AD与BE交于点P,那么AD与BE的位置关系是否发生变化,说明理由.
(1)、求证:AD=BE;(2)、试说明AD平分∠BAE.(3)、如图2,将△CDE绕着点C旋转一定的角度,AD与BE交于点P,那么AD与BE的位置关系是否发生变化,说明理由.