江西省抚州市2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-07-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、 $x^{2} + x^{3} = x^{5}$ B、 ${(x^{2})}^{2} + x^{4} = 2 x^{4}$ C、 ${(3 x)}^{2} = 6 x^{2}$ D、 ${(x^{2})}^{3} = x^{5}$

查看试题解析
2. 北京春夏之季鲜花烂漫，空气中弥漫着各种花粉，有一种花粉的直径是0.000063米，将0.000063用科学记数法表示应为（　　）

A、6.3×10^﹣4 B、0.63×10^﹣4 C、6.3×10^﹣5 D、63×10^﹣5

查看试题解析
3. 如图，已知 $A E = A C$ ， $∠ C = ∠ E$ ，若 $∠ 1 = ∠ 2$ 可得 $△ A B C ≌ △ A D E$ ，则判定这两个三角形全等的依据是（）

A、SSS B、ASA C、SAS D、AAS

查看试题解析
4. 如图1，将一张长方形纸板四角各切去一个同样的正方形，制成如图2的无盖纸盒，若该纸盒的容积为4a²b则图2中纸盒底部长方形的周长为（）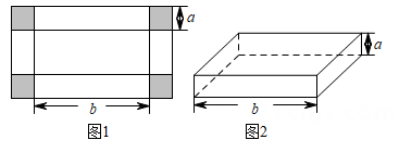

A、4ab B、8ab C、4a+b D、8a+2b

查看试题解析
5. 中国滑雪天才少女谷爱凌在2022年北京冬奥会的赛场上斩获“自由式滑雪大跳台”首金，这是她获得的首个冬奥会奖牌，也是中国运动员第一次参加冬奥会大跳台的比赛．项目图标如下图；则在下列判断中①∠1与∠2是对顶角；②∠3与∠4是同旁内角；③∠5与∠6是同旁内角；④∠1与∠4是内错角，其中正确的有（）个．

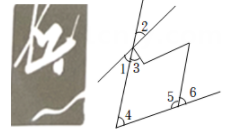A、1 B、2 C、3 D、4

查看试题解析
6. 如图所示的图象（折线ABCDE）描述了一辆汽车在某一直线上的行驶过程中，汽车离出发地的距离s（千米）与行驶时间t（时）之间的关系，根据图象信息，下列说法正确的是（）

A、汽车共行驶了140千米 B、汽车在行驶途中停留了1小时 C、汽车在整个行驶过程中的平均速度为30千米/时 D、汽车出发后6小时至9小时之间行驶的速度在逐渐减小

查看试题解析

二、填空题

7. 一名老师带领x名学生到动物园参观，已知成人票每张30元，学生票每张10元，设门票的总费用为y元，则y与x的函数关系式为 .

查看试题解析
8. 我国传统的木结构房屋，窗子常用各种图案装饰，如图是一种常见的图案，这种图案有条对称轴．

查看试题解析
9. 某超市举行有奖促销活动：凡一次性购物满300元者即可获得一次摇奖机会，摇奖机是一个如图的圆形转盘，被分成16等份，指针分别指向红、黄、蓝色区域，依次可获一、二、三等奖，则购物满300元者获得二等奖的概率是．

查看试题解析
10. 如图，把一张长方形纸片ABCD沿EF折叠，若 $∠ 2 = 42 °$ ，则∠1的度数为．

查看试题解析
11. 已知等腰三角形两边的长分别为a，b，且满足 $| a - 3 | + {(b - 7)}^{2} = 0$ ．则这个等腰三角形的周长为．

查看试题解析
12. 已知 $∠ A B C = 30 °$ ，点P是射线BC上一动点，把 $△ A B P$ 沿AP折叠，B点的对应点为点D，当 $△ A B P$ 是等腰三角形时， $∠ A B D$ 的度数为．

查看试题解析

三、解答题

13. 计算：

(1)、 $- 1^{2022} + {(π - 3)}^{0} - {(- \frac{3}{2})}^{- 2}$

(2)、 ${(2 m n^{2})}^{4} \cdot (- 6 m^{2} n) \div (- 3 m^{3} n^{7})$

查看试题解析
14. 已知：如图， $∠ 1 = ∠ 2$ ， $∠ 3 = ∠ B$ ， $∠ 4 = ∠ 5$ ．试说明： $A D ∥ E F$ ．请完成下列填空．
解：因为 $∠ 1 = ∠ 2$ ，所以  ▲   $∥ A B$ ．
所以 $∠ 3 =$   ▲  （   ）．
又因为 $∠ 3 = ∠ B$ ，所以 $∠ B =$   ▲   ．
所以  ▲   $∥ B C$ （   ）．
所以 $∠ 5 = ∠ D H E$ ，
又因为 $∠ 4 = ∠ 5$ ，所以 $∠ 4 = ∠ D H E$ ，所以 $A D ∥ E F$ ．

查看试题解析
15. 如图，在 $6 \times 6$ 的正方形网格中，A，B，C点均是格点，仅用无刻度直尺，分别按要求作图．

(1)、在图1中过点C作出直线AB的垂线CE；

(2)、在图2中标出格点D，作一条射线AD，使得 $∠ D A B = 45 °$ ．

查看试题解析
16. 先化简，再求值： ${(x - 2)}^{2} + (2 x + 3) (2 x - 3) - x (3 x - 2)$ ，其中 $x = - 1$ ．

查看试题解析
17. 如图，点E是 $△ A B C$ 的边AC的反向延长线上一点， $A D ⊥ B C$ 于点D， $E G ⊥ B C$ 于点G， $∠ E = ∠ 3$ ．
请问：AD平分 $∠ B A C$ 吗？请说明理由．

查看试题解析
18. 为了配合抚州市全员核酸检测，在停课不停学期间，某校提供“录播”和“直播”两种教学方式让学生进行居家线上学习．为了了解该校学生线上学习参与度情况，从接受这两种教学方式的学生中，分别随机抽取50名进行调查，调查结果如下表（数据分组包含左端值不包含右端值）．
参与度
人数
教学方式
0~20%
20%~50%
50%~80%
80%~100%
录播
5
18
14
13
直播
2
15
21
12

(1)、从选择教学方式为“录播”的学生中任意抽取1名学生，估计该生的参与度不低于50%的概率是多少？

(2)、若该校共有2400名学生，选择“录播”和“直播”的人数之比为 $3 ： 5$ ，试估计选择教学方式为“直播”的学生参与度在20%以下的共有多少人？

查看试题解析
19. 如图所示，已知等腰 $R t △ A B C$ 中， $A C = B C$ ， $∠ A C B = 90 °$ ，点D是AB上一点，且 $A D < B D$ ， $A E ⊥ C D$ 于E， $B F ⊥ C E$ 于F．

(1)、试说明： $△ A C E ≌ △ C B F$ ；

(2)、若 $A E = 2 c m$ ， $B F = 6 c m$ ，求EF的长度．

查看试题解析
20. “双减”政策下，孩子们的课余支配时间更多了．肖强每周都会去图书馆看课外书．这个周末，他早晨8时从家出发步行去图书馆．途中发现忘了带借书证，于是原路原速返回，同时电话联系爸爸．爸爸马上骑自行车送借书证并在路上遇见肖强．为了多一些阅读时间，爸爸按原速骑自行车送肖强去图书馆．肖强离家的距离s（m）与时间t（min）之间的关系如图所示．请根据图中所提供的信息，回答下列问题：

(1)、图象中自变量是，因变量是；

(2)、肖强步行的速度是m/min，爸爸骑自行车的速度是m/min；

(3)、肖强离家m时遇到爸爸，图书馆离肖强家有m；

(4)、写出爸爸骑自行车送肖强去图书馆时肖强离家的距离s与时间t之间的关系式．

查看试题解析
21. 一副常规直角三角板中的直角顶点C按如图方式叠放在一起，已知 $∠ A = 60 °$ ， $∠ D = 30 °$ ， $∠ E = ∠ B = 45 °$ ．

(1)、若 $∠ D C E = 30 °$ ，则 $∠ A C B$ 的度数为；

(2)、由（1）猜想 $∠ A C B$ 与 $∠ D C E$ 的数量关系，并说明理由；

(3)、若 $∠ A C E < 90 °$ 且点E在直线AC的上方，当这两块直角三角板有一组边互相平行时，请求出 $∠ A C E$ 角度所有可能的值．

查看试题解析
22. 阅读下列材料：利用完全平方公式，将多项式 $x^{2} + b x + c$ 变形为 ${(x + m)}^{2} + n$ 的形式，然后由 ${(x + m)}^{2} \geq 0$ 就可求出多项式 $x^{2} + b x + c$ 的最小值．
例题：求 $x^{2} - 12 x + 37$ 的最小值．

解： $x^{2} - 12 x + 37 = x^{2} - 2 x \cdot 6 + 6^{2} - 6^{2} + 37 = {(x - 6)}^{2} + 1$ ．

因为不论x取何值， ${(x - 6)}^{2}$ 总是非负数，即 ${(x - 6)}^{2} \geq 0$ ．

所以 ${(x - 6)}^{2} + 1 \geq 1$ ．

所以当 $x = 6$ 时， $x^{2} - 12 x + 37$ 有最小值，最小值是1.

根据上述材料，解答下列问题：

(1)、填空： $x^{2} - 6 x +$ =（x-）² ．

(2)、将 $x^{2} + 10 x - 2$ 变形为 ${(x + m)}^{2} + n$ 的形式，并求出 $x^{2} + 10 x - 2$ 的最小值．

(3)、如图所示的第一个长方形边长分别是 $2 a + 5$ 、 $3 a + 2$ ，面积为 $S_{1}$ ；如图所示的第二个长方形边长分别是 $5 a$ 、 $a + 5$ ，面积为 $S_{2}$ ．试比较 $S_{1}$ 与 $S_{2}$ 的大小，并说明理由．

查看试题解析
23. 如图1，在四边形ABDC中， $C D = B D$ ， $∠ A = ∠ C D B = 90 °$ ，点E是AC上一点，点F是AB的延长线上一点，且 $C E = B F$ ．

(1)、试说明： $D E = D F$ ．

(2)、如图2，若点G在AB上，且 $∠ E D G = 45 °$ ，试猜想CE，EG，BG之间的数量关系，并加以说明．

(3)、如图3，若题目中的 $∠ A = ∠ C D B = 90 °$ 改成 $∠ A = α$ ， $∠ C D B = 180 ° - α$ ，点G在AB上，则 $∠ E D G$ 满足什么条件时，（2）中的结论仍然成立？（直接写出条件即可）（提示：四边形的内角和等于360°）

查看试题解析