广东省中山市2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-07-28 类型：期末考试

进入出卷网下载

一、单选题

1. 为了描述某病人的体温变化情况，以下统计图最合适的是（）

A、扇形统计图 B、条形统计图 C、折线统计图 D、直方图

查看试题解析
2. 平面直角坐标系中，下列点中不在坐标轴上的是（）

A、（0，0） B、（0，－1） C、（－2，0） D、（1，－1）

查看试题解析
3. 下列命题中，假命题是（）

A、同旁内角相等，两直线平行 B、在同一平面内，垂直于同一条直线的两条直线平行 C、平行于同一条直线的两条直线平行 D、两直线平行，同旁内角互补

查看试题解析
4. 若m>n ，则下列不等式中一定成立的是（）

A、m+2<n+3 B、2m<3n C、-m<-n D、ma²>na²

查看试题解析
5. 以下调查中，适宜抽样调查的是（）

A、调查“神舟十四号”零部件的可靠性 B、调查某批次汽车的抗撞击能力 C、乘飞机旅客的安检 D、选出某校短跑最快的学生参加比赛

查看试题解析
6. 已知关于x，y的方程组 ${\begin{array}{l} 3 x + y = 1 + 3 a \\ x + 3 y = 1 - a \end{array}$ 的解满足x＋y＝0，则a等于（）

A、1 B、0 C、－1 D、－2

查看试题解析
7. 一个正方体的体积为63，则它的棱长a的取值范围是（）

A、3＜a＜4 B、4＜a＜5 C、7＜a＜8 D、8＜a＜9

查看试题解析
8. 如图，DE∥BA，DF∥CA．与∠A不一定相等的角是（）

A、∠BFD B、∠CED C、∠ABC D、∠EDF

查看试题解析
9. 下面两个统计图反映的是甲、乙两所学校三个年级的学生在各校学生总人数中的占比情况，下列说法错误的是（）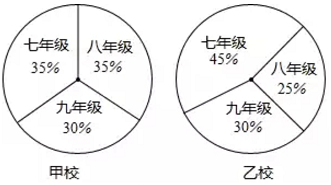

A、甲校中七年级学生和八年级学生人数一样多 B、乙校中七年级学生人数最多 C、乙校中八年级学生比九年级学生人数少 D、甲、乙两校的九年级学生人数一样多

查看试题解析
10. 若关于x的不等式组 ${\begin{array}{l} x > 2 \\ x > a \end{array}$ 的解集是x＞a，则（）

A、a＞2 B、a≥2 C、a＜2 D、a≤2

查看试题解析

二、填空题

11. 5的平方根是．

查看试题解析
12. 一个数的立方根是－2，则这个数是．

查看试题解析
13. 已知 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ 是二元一次方程 $a x + 2 y = 6$ 的一个解，则a＝．

查看试题解析
14. 在平面直角坐标系中，将点A（－3，2）向右平移2个单位长度，再向下平移3个单位长度后得到点A′的坐标是．

查看试题解析
15. 如图，两面平面镜OA、OB形成∠AOB，从OB上一点E射出的一条光线经OA上一点D反射后的光线DC恰好与OB平行，已知∠AOB＝35°，∠ODE＝∠ADC，则∠DEB的度数是．

查看试题解析
16. 我国古代数学书《四元玉鉴》中有这样一个问题：“九百九十九文钱，甜果苦果买一千，甜果九个十一文，苦果七个四文钱”．计算可得甜果的个数是．

查看试题解析
17. 平面直角坐标系中有两点A（m，－1），B（3，4），当m取任意实数时，线段AB长度的最小值为．

查看试题解析

三、解答题

18. 计算： $\sqrt{16}$ ＋ $\sqrt[3]{- 8}$ ＋| $\sqrt{5}$ －3|－（2－ $\sqrt{5}$ ）

查看试题解析
19. 解不等式 $\frac{x + 5}{4} - \frac{2 x + 3}{6} \geq 1$ ，并把它的解集在数轴上表示出来．

查看试题解析
20. 解方程组： ${\begin{array}{l} 2 (x - y) - (x + y) = - 2 \\ 3 (x + y) - 2 (2 x - y) = 8 \end{array}$

查看试题解析
21. 如图，直线AB，CD相交于点O，OE平分∠BOC，OF⊥CD，若∠BOE＝72°，求∠AOF的度数．

查看试题解析
22. 平面直角坐标系中，点A坐标为（2m－3，3m＋2）．

(1)、若点A在坐标轴上，求m的值：

(2)、若点A在第二象限内，求m的取值范围．

查看试题解析
23. 为了解某校1200名学生平均每天课外阅读的时间，随机调查了部分学生一周内平均每天课外阅读的时间（单位：分钟），将有关数据统计整理如下图表．请根据图表中所提供的信息，解答下列问题：
组别
时间
频数
百分比
1
15~25
7
14%
2
25~35
a
24%
3
35~45
20
40%
4
45~55
6
b
5
55~65
5
10%
（注：每组数据包括最小值，不包括最大值）

(1)、a＝， b＝；

(2)、补全频数分布直方图；

(3)、估计该校平均每天课外阅读时间少于35分钟的学生有多少人？

查看试题解析
24. 在某次知识竞赛中，甲、乙两人轮流答题，每人都要回答20道题，每道题回答符合题意得m分，回答不符合题意或放弃回答扣n分．当甲、乙两人恰好都答完12道题时，甲答对了9道题，得分为45分；乙答对了10道题，得分为54分．

(1)、求m和n的值；

(2)、假如最后得分不低于70分就能晋级，甲在剩下的比赛中至少还要答对多少道题才能顺利晋级？

查看试题解析
25. 如图，直线a∥b，点A、B在直线a上，点C、D在直线b上，连接AD、BC，BE平分∠ABC，DE平分∠ADC，BE、DE所在直线相交于点E，设∠ABC＝ $α$ ， ∠ADC＝ $β$ ．

(1)、如图1，当点B在点A的左侧时，探究∠BED与 $α$ 、 $β$ 之间的关系并加以证明：

(2)、如图2，当点B在点A的右侧时，（1）中关系是否依然成立？说明理由．

查看试题解析

组别	时间	频数	百分比
1	15~25	7	14%
2	25~35	a	24%
3	35~45	20	40%
4	45~55	6	b
5	55~65	5	10%