安徽省蚌埠市2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-07-28 类型:期末考试
一、单选题
-
1. 在0、π、0.0101101110…(每两个0之间的1依次增加)、﹣3.14、中,无理数的个数有( )A、4个 B、3个 C、2个 D、1个2. 下列计算正确的是( )A、 B、 C、 D、3. 清代袁枚的《苔》中的诗句:“白日不到处,青春恰自来,苔花如米小,也学牡丹开” .已知苔花的花粉非常小,直径约为0.000085米,则数据0.000085用科学记数法可表示为( )A、 B、 C、 D、4. 实数a,b在数轴上的对应点的位置如图,下列关系式不成立的是( )
 A、3a>3b B、1﹣a<0 C、a﹣1>b﹣1 D、﹣a>﹣b5. 用四根火柴棒可摆成如图所示的象形字“口”,平移此象形字火柴棒后,变成的象形字是( )
A、3a>3b B、1﹣a<0 C、a﹣1>b﹣1 D、﹣a>﹣b5. 用四根火柴棒可摆成如图所示的象形字“口”,平移此象形字火柴棒后,变成的象形字是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 如图,将一张边长为x的正方形纸板按图中虚线裁剪成三块长方形,观察图形表示阴影部分的面积,则表示错误的是( )
6. 如图,将一张边长为x的正方形纸板按图中虚线裁剪成三块长方形,观察图形表示阴影部分的面积,则表示错误的是( ) A、 B、 C、 D、7. 如图,如果AB∥EF,EF∥CD,下列各式正确的是( )
A、 B、 C、 D、7. 如图,如果AB∥EF,EF∥CD,下列各式正确的是( ) A、∠1+∠2−∠3=90° B、∠1−∠2+∠3=90° C、∠1+∠2+∠3=90° D、∠2+∠3−∠1=180°8. 已知关于x的分式的解为非负数,则a的范围为( )A、且 B、且 C、且 D、且9. 已知, , , 现将两块直角三角板OAB()和直角三角板OCD()按如图所示放置,直角顶点O重合,点A,D在EF上,若 , , 则的度数为( )
A、∠1+∠2−∠3=90° B、∠1−∠2+∠3=90° C、∠1+∠2+∠3=90° D、∠2+∠3−∠1=180°8. 已知关于x的分式的解为非负数,则a的范围为( )A、且 B、且 C、且 D、且9. 已知, , , 现将两块直角三角板OAB()和直角三角板OCD()按如图所示放置,直角顶点O重合,点A,D在EF上,若 , , 则的度数为( )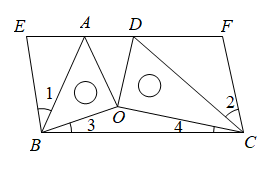 A、110° B、115° C、120° D、140°10. 已知实数 , 满足 , 则下列结论中错误的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
A、110° B、115° C、120° D、140°10. 已知实数 , 满足 , 则下列结论中错误的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则二、填空题
-
11. x=1时,分式 无意义,则a=.12. 分解因式: .13. 如图,为一长条形纸带, , 将沿折叠,A、D两点分别与、对应,若 , 则的度数为 .
 14. 若实数x满足 , 则 .15. 如图1为北斗七星的位置图,如图2将北斗七星分别标为A,B,C,D,E,F,G,将A,B,C,D,E,F顺次首尾连接,若AF恰好经过点G,且 , , .
14. 若实数x满足 , 则 .15. 如图1为北斗七星的位置图,如图2将北斗七星分别标为A,B,C,D,E,F,G,将A,B,C,D,E,F顺次首尾连接,若AF恰好经过点G,且 , , .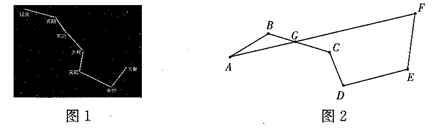 (1)、的度数为;(2)、计算的度数是 .
(1)、的度数为;(2)、计算的度数是 .三、解答题
-
16. 计算:(1)、;(2)、 .17. 解方程(不等式组)(1)、解方程:;(2)、解不等式组18. 先化简,再求值: ,其中 满足 .19. 已知,平分 , 平分.(1)、如图1,若 , , 求的度数;
 (2)、如图2,若 , , 求的度数.
(2)、如图2,若 , , 求的度数. 20. 我市某实验学校为了落实“大阅读工程”,培育校园文化氛围.去年购买了一批图书.其中古典名著书的单价比现代文学书的单价多4元,用1200元购买的古典名著书与用800元购买的现代文学书数量相等.(1)、求去年购买的古典名著书和现代文学书的单价各是多少元?(2)、若今年现代文学书的单价比去年提高了25%,古典名著书的单价与去年相同,这所学校今年计划再购买这两类图书共200本,且购买现代文学书和古典名著书的总费用不超过2122元,这所中学今年至少要购买多少本现代文学书?21. 如图①,已知AD∥BC,∠B=∠D=120°.
20. 我市某实验学校为了落实“大阅读工程”,培育校园文化氛围.去年购买了一批图书.其中古典名著书的单价比现代文学书的单价多4元,用1200元购买的古典名著书与用800元购买的现代文学书数量相等.(1)、求去年购买的古典名著书和现代文学书的单价各是多少元?(2)、若今年现代文学书的单价比去年提高了25%,古典名著书的单价与去年相同,这所学校今年计划再购买这两类图书共200本,且购买现代文学书和古典名著书的总费用不超过2122元,这所中学今年至少要购买多少本现代文学书?21. 如图①,已知AD∥BC,∠B=∠D=120°. (1)、请问:AB与CD平行吗?为什么?(2)、若点E、F在线段CD上,且满足AC平分∠BAE,AF平分∠DAE,如图②,求∠FAC的度数.
(1)、请问:AB与CD平行吗?为什么?(2)、若点E、F在线段CD上,且满足AC平分∠BAE,AF平分∠DAE,如图②,求∠FAC的度数. (3)、若点E在直线CD上,且满足∠EAC=∠BAC,求∠ACD:∠AED的值(请自己画出正确图形,并解答).
(3)、若点E在直线CD上,且满足∠EAC=∠BAC,求∠ACD:∠AED的值(请自己画出正确图形,并解答).