安徽省安庆市2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-07-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列说法正确的是（）

A、无限小数都是无理数 B、无理数都是无限小数 C、带根号的数都是无理数 D、所有有理数都可以用数轴上的点表示，反过来，数轴上的所有点都表示有理数

查看试题解析
2. 估计 $\sqrt{29}$ 的值在（）

A、2和3之间 B、3和4之间 678 C、4和5之间 D、5和6之间

查看试题解析
3. “ $K N 95$ ”表示此类型的口罩能过滤空气中 $95 %$ 的粒径约为 $0.0000003 m$ 的非油性颗粒，其中 $0.0000003$ 用科学记数法表示为（）．

A、 $3 \times 1 0^{- 6}$ B、 $3 \times 1 0^{- 7}$ C、 $0.3 \times 1 0^{- 6}$ D、 $0.3 \times 1 0^{- 7}$

查看试题解析
4. 某不等式的解在数轴上表示如图，则该不等式的解是（）

A、 $x \leq 3$ B、 $x < 3$ C、 $x \geq 3$ D、 $x > 3$

查看试题解析
5. 计算 $a \cdot (- a^{2})^{3}$ 的结果是（）.

A、 $a^{6}$ B、 $- a^{6}$ C、 $a^{7}$ D、 $- a^{7}$

查看试题解析
6. 约分 $\frac{- a^{2} b}{5 a b^{2}}$ 的结果是（）

A、 $- \frac{1}{5}$ B、 $- \frac{a}{5 b}$ C、 $- \frac{1}{5 b}$ D、 $- \frac{1}{5 a}$

查看试题解析
7. 将 $m^{3} n - m n$ 进行因式分解，正确的是（）

A、 $m (m^{2} n - n)$ B、 $m n (m - 1)^{2}$ C、 $m n (m + 1) (m - 1)$ D、 $m n (m^{2} - 1)$

查看试题解析
8. 为了响应组织部开展的“百万消费助农”活动，小明的妈妈在“河南消费惠农网”花了120元钱购买了一批拖鞋，在“豫扶网”她发现同类的拖鞋单价每双少了5元，于是又花了100元钱购买了一批同类的鞋子，且比上次还多买了两双．并把购买的鞋子全部赠给敬老院．若设第一批鞋子每双x元，则可以列出方程为（）

A、 $\frac{120}{x} = \frac{100}{x + 5} + 2$ B、 $\frac{120}{x} = \frac{100}{x - 5} + 2$ C、 $\frac{120}{x} = \frac{100}{x + 5} - 2$ D、 $\frac{120}{x} = \frac{100}{x - 5} - 2$

查看试题解析
9. 如图，将一块含有45°角的直角三角板放置在两条平行线上，若∠1=25°，则∠2为（）

A、15° B、20° C、25° D、30°

查看试题解析
10. 在矩形 $A B C D$ 内，将两张边长分别为 $a$ 和 $b (a > a)$ 的正方形纸片按图①，图②两种方式放置（图①，图②中两张正方形纸片均有部分重叠），矩形中未被这两张正方形纸片覆盖的部分用阴影表示，若图①中阴影部分面积为 $S_{1}$ ，图②中阴影部分的面积和为 $S_{2}$ .则 $S_{1} - S_{2}$ 的值表示正确的是（）

A、 $B E \cdot F G$ B、 $M N \cdot F G$ C、 $B E \cdot G D$ D、 $M N \cdot G D$

查看试题解析

二、填空题

11. 已知一个正数 $x$ 的两个平方根分别是 $a + 1$ 和 $2 a - 7$ ，则 $a =$ ，正数 $x =$ ．

查看试题解析
12. 已知a、b满足（a﹣1）²+ $\sqrt{b + 2}$ =0，则a+b= ．

查看试题解析
13. 如图，边长分别为a、b的两个正方形并排放在一起，当 $a + b = 8$ ， $a b = 10$ ，时阴影部分的面积为．

查看试题解析
14. 已知： $A B / / C D$ ，点 $C$ 在点 $D$ 的右侧， $B E$ 平分 $∠ A B C$ ， $D E$ 平分 $∠ A D C$ ， $B E$ ， $D E$ 所在直线交于点 $E$ ， $∠ A D C = 70 °$ ．

(1)、 $∠ C D E =$ 度；

(2)、若 $∠ A B C = n °$ ，则 $∠ B E D$ 的度数是（用含 $n$ 的式子表示）．

查看试题解析

三、解答题

15. 计算题：

(1)、 $(- 3)^{2} + (5 - π)^{0} - | - 4 | + (\frac{1}{3})^{- 2}$

(2)、 $2 \cdot (- a^{2} b)^{2} \cdot \frac{1}{2} b^{3} + (2 a b)^{5} \div 8 a$

查看试题解析
16. 计算 $\frac{a}{a - 1} - \frac{3 a - 1}{a^{2} - 1}$ ．

查看试题解析
17. 观察以下等式：
第1个等式： $\frac{2}{3^{2} - 4} \times (2 - \frac{1 - 4}{1}) = \frac{2}{1}$ ；
第2个等式： $\frac{4}{4^{2} - 4} \times (2 - \frac{2 - 4}{2}) = \frac{2}{2}$ ；
第3个等式： $\frac{6}{5^{2} - 4} \times (2 - \frac{3 - 4}{3}) = \frac{2}{3}$ ；
第4个等式： $\frac{8}{6^{2} - 4} \times (2 - \frac{4 - 4}{4}) = \frac{2}{4}$ ；
第5个等式： $\frac{10}{7^{2} - 4} \times (2 - \frac{5 - 4}{5}) = \frac{2}{5}$ ；……
按照以上规律，解决下列问题：

(1)、写出第6个等式：；

(2)、写出你猜想的第n个等式：（用含 $n$ 的等式表示），并证明．

查看试题解析
18. 解不等式组 ${\begin{array}{l} 2 (x + 1) > x \\ 3 x - 1 \leq \frac{- x - 9}{2} \end{array}$ ，并在数轴上表示他的解集．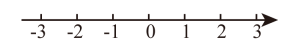

查看试题解析
19. 如图，三角形ABC在如图方格纸中，方格纸中的每个小方格都是边长为1个单位长度的正方形．

(1)、把三角形ABC先向上平移3个单位，再向右平移2个单位得到三角形 $A^{'} B^{'} C^{'}$ ，请在图中画出三角形 $A^{'} B^{'} C$ ；

(2)、计算三角形ABC的面积．

查看试题解析
20. 如图，点 $O$ 是直线AB上一点，OD平分∠AOC，∠BOE=3∠COE，∠DOE=81°，求∠BOE，∠AOD的度数.

查看试题解析
21. 完成下面的证明．
如图， $E$ ， $F$ 分别在 $A B$ 和 $C D$ 上， $∠ 1 = ∠ D$ ， $∠ 2$ 与 $∠ C$ 互余， $A F ⊥ C E$ 于点 $G$ ．求证 $A B ∥ C D$ ．
证明：∵ $A F ⊥ C E$ （已知），
∴ $∠ C G F = 90 °$ （垂直的定义）．
∵ $∠ 1 = ∠ D$ （已知），
∴  ▲  ∥  ▲  （   ）．
∴ $∠ 4 = ∠ C G F = 90 °$ （   ）．
又∵ $∠ 2 + ∠ C = 90 °$ （已知），
$∠ 2 + ∠ 3 + ∠ 4 =$   ▲  （平角的定义），
∴ $∠ 2 + ∠ C = ∠ 2 + ∠ 3 = 90 °$ ．
∴ $∠ C =$   ▲   ．
∴ $A B ∥ C D$ （   ）．

查看试题解析
22. 为了深入贯彻习总书记关于“双减”工作的重要指示，增强学生的体质，济南市某中学决定购买一些篮球和足球来促进学生的体育锻炼，已知每个篮球的售价比每个足球的售价单价多20元，并且花费6000元购买篮球的数量是花费3200元购买足球数量的1.25倍．

(1)、求篮球和足球的单价分别是多少元？

(2)、根据学校的实际需求，需要一次性购买篮球和足球共200个，并且要求购买篮球和足球的总费用不超过9600元，那么学校最少购入多少个足球？

查看试题解析
23. 若x满足 $(9 - x) (x - 4) = 4$ ，求 ${(4 - x)}^{2} + {(x - 9)}^{2}$ 的值．
解：设 $9 - x = a ， x - 4 = b$ ，
则 $(9 - x) (x - 4) = a b = 4 ， a + b = (9 - x) + (x - 4) = 5$ ，
∴ ${(4 - x)}^{2} + {(x - 9)}^{2} = a^{2} + b^{2} = {(a + b)}^{2} - 2 a b = 5^{2} - 2 \times 4 = 17$ ．
请仿照上面的方法求解下面问题：

(1)、若x满足 ${(x - 2004)}^{2} + {(x - 2007)}^{2} = 31$ ，求 $(x - 2004) (x - 2007)$ 的值；

(2)、已知正方形 $A B C D$ 的边长为x，E，F分别是 $A D ， D C$ 上的点，且 $A E = 1 ， C F = 3$ ，长方形 $E M F D$ 的面积是48，分别 $M F ， D F$ 作正方形 $M F R N$ 和正方形 $G F D H$ ，求阴影部分的面积．

查看试题解析