云南省昭通市2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-07-27 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，将平行四边形ABCD的一边BC延长至点E．若 $∠ A = 105 °$ ，则 $∠ B C D =$ （）

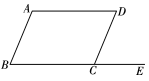A、60° B、75° C、80° D、105°

查看试题解析
2. 下列说法中正确的是（）

A、三角形的三条中线必交于一点 B、直角三角形只有一条高 C、三角形的中线可能在三角形的外部 D、三角形的高线都在三角形的内部

查看试题解析
3. 下列运算中，正确的是（）

A、 ${(π - 3.14)}^{0} = 0$ B、 ${(- 2)}^{- 2} = 4$ C、 $\sqrt{(- 2)} \cdot \sqrt{(- 8)} = 4$ D、 $\sqrt{{(- 3)}^{2}} = 3$

查看试题解析
4. 如果正比例函数 $y = k x (k \neq 0)$ 的图象经过第二、四象限，那么一次函数 $y = k x + k$ 的图象经过（）

A、第一、二、三象限 B、第二、三、四象限 C、第一、二、四象限 D、第一、三、四象限

查看试题解析
5. △ABC的三边分别为a，b，c，下列条件中，不能判断△ABC是直角三角形的是（）

A、 $∠ A + ∠ B = ∠ C$ B、 $∠ A ： ∠ B ： ∠ C = 3 ： 4 ： 5$ C、 $a ： b ： c = 3 ： 4 ： 5$ D、 $a ： b ： c = 1 ： 2 ： \sqrt{3}$

查看试题解析
6. 二次根式 $\sqrt{\frac{1}{3}}$ ， $\sqrt{18}$ ， $\sqrt{30}$ ， $\sqrt{11 x^{2}}$ ， $\sqrt{x^{2} - y^{2}}$ 中，最简二次根式有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 观察下列一组数： $- \frac{3}{2}$ ， $\frac{5}{4}$ ， $- \frac{7}{6}$ ， $\frac{9}{8}$ ， $- \frac{11}{10}$ ， …，它们是按一定规律排列的，那么这组数的第2022个数是（）

A、 $- \frac{2022}{2021}$ B、 $\frac{2024}{2023}$ C、 $- \frac{4043}{4044}$ D、 $\frac{4045}{4044}$

查看试题解析
8. 如图，在菱形ABCD中，对角线AC，BD相交于点O，点E，F分别是AB，AO的中点，连接EF，若 $O A = 3$ ， $E F = 2$ ，则菱形ABCD的边长为（）

A、2 B、2.5 C、3 D、5

查看试题解析
9. 如图，直线 $y_{1} = a x + b$ 与 $y_{2} = m x + n$ 相交于点P，点P的横坐标为 $- 1$ ，则关于x的不等式 $a x + b \leq m x + n$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
10. 已知 $x + y = - 6$ ， $x y = 8$ ，则 $x^{2} + y^{2}$ 的值为（）

A、36 B、32 C、20 D、8

查看试题解析
11. 如图，在△ABC中，BD平分 $∠ A B C$ ，点E在BC的垂直平分线上，若 $∠ A = 60 °$ ， $∠ A B D = 24 °$ ，则 $∠ A C E$ 的度数为（）

A、48° B、50° C、55° D、60°

查看试题解析
12. 如图，在正方形ABCD中，AC为对角线，E为AB上一点，过点E作EF∥AD，与AC、DC分别交于点G、F，H为CG的中点，连接DE、EH、DH、FH．下列结论：① $G E = F D$ ；② $A G = D H$ ；③ $∠ H E A + ∠ H D A = 180 °$ ；④ $△ E H F ≌ △ D H C$ ，其中结论正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 若 $\sqrt{3 - x}$ 在实数范围内有意义，则 $x$ 的取值范围是.

查看试题解析
14. 如图，在△ABC中， $∠ C = 90 °$ ， AD平分 $∠ B A C$ ，若 $C D = 3 c m$ ， $A B = 10 c m$ ，则△ABD的面积为 $c m^{2}$ ．

查看试题解析
15. 因式分解： $2 x^{2} - 2 =$ ；

查看试题解析
16. 一个多边形的每一个外角都等于45°，则这个多边形的内角和为

查看试题解析
17. 如图，在Rt△ABC中， $∠ A C B = 90 °$ ， $C D ⊥ A B$ 于点D， $∠ A C D = 3 ∠ B C D$ ， E是斜边AB的中点，则 $∠ E C A =$ ．

查看试题解析
18. 如图，在矩形纸片ABCD中， $A B = 3$ ，点E、F分别是AB和CD的中点，H为BC上的一点，现将△ABH沿AH折叠，使点B落在直线EF上的点G处，当△ADG为等腰三角形时， $A D =$ ．

查看试题解析

三、解答题

19.

(1)、计算： $\sqrt{8} \times \sqrt{6} - \sqrt{24} \div \sqrt{2} + \sqrt{\frac{1}{3}}$ ；

(2)、化简： $(a - 2 + \frac{3}{a + 2}) \div \frac{a^{2} + 2 a + 1}{a + 2}$ ．

查看试题解析
20. 为弘扬民族精神，传播传统文化，某县教育系统将组织“弘扬传统文件化，永承华夏辉煌”的演讲比赛．某校各年级共推荐了19位同学参加初赛（校级演讲比赛），初赛成绩排名前10的同学进入决赛．

(1)、若初赛结束后，每位同学的分数互不相同．某同学知道自己的分数后，要判断自己能否进入决赛，他只需知道这19位同学成绩的；（填：平均数或众数或中位数）

(2)、若初赛结束后，这19位同学的成绩如下：
签号
1
2
3
4
5
6
7
8
9
10
成绩
8.5
9.1
9.2
8.6
9.3
8.8
9.6
8.9
8.7
9.7
签号
11
12
13
14
15
16
17
18
19
成绩
9.8
9.1
8.9
9.3
9.6
8.8
9
8.7
9.3
2号选手笑着说：“我的成绩代表着咱们这19位同学的平均水平呀！”
14号选手说：“与我同分数的选手最多，我的成绩代表着咱们这19位选手的大众水平嘛！”
请问，这19位同学成绩的平均数为，众数为；

(3)、已知10号选手与15号选手经常参加此类演讲比赛，她俩想看看近期谁的成绩较好、较稳定，她俩用近三次同时参加演讲比赛的成绩计算得到平均分一样，10号选手的方差为0.5，15号选手的方差为0.38．你认为号选手的成绩比较稳定．

查看试题解析
21. 如图所示，在平面直角坐标系中，已知△ABC的三个顶点坐标分别是 $A (- 3 ， 0)$ ， $B (- 5 ， - 2)$ ， $C (- 2 ， - 5)$ ．

(1)、请画出与△ABC关于x轴对称的 $△ A B^{'} C^{'}$ ；

(2)、在y轴上找一点P，使 $P A + P C$ 最小，求点P的坐标．

查看试题解析
22. 如图，直线AB，CD相交于点E， $A D = B C$ ， $A D ∥ B C$ ．

(1)、求证： $A E = B E$ ；

(2)、连接AC，BD，当 $∠ A E C = 90 °$ 时，判断四边形ADBC的形状，并请证明你的结论．

查看试题解析
23. 某超市计划购进甲、乙两种水果进行销售，经了解，甲种水果的进价比乙种水果的进价每千克少4元，且用6400元购进甲种水果的数量与用8000元购进乙种水果的数量一样多．

(1)、求甲、乙两种水果每千克的进价分别是多少元？

(2)、该超市根据平常的销售情况确定，购进两种水果共2000千克，其中甲种水果的数量不超过乙种水果数量的3倍，且购买资金不超过34200元．购回后，该超市决定将甲种水果的销售价定为每千克20元，乙种水果的销售价定为每千克25元，则该超市应如何进货，才能获得最大利润，最大利润是多少？

查看试题解析
24. 如图，已知O是坐标原点，点A的坐标是 $(6 ， 0)$ ，点B是y轴正半轴上一动点，以OB，OA为边作矩形OBCA，OC是矩形OBCA的对角线，OE平分 $∠ B O C$ 交BC于点E，CF平分 $∠ A C O$ 交OA于点F．

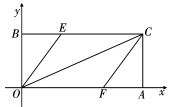(1)、求证：四边形OECF是平行四边形；

(2)、当四边形OECF为菱形时，求点B的坐标；

(3)、过点E作 $E G ⊥ O C$ ，垂足为点G，过点F作 $F H ⊥ O C$ ，垂足为点H，当点G，H将对角线OC三等分时，求点B的坐标．

查看试题解析

签号	1	2	3	4	5	6	7	8	9	10
成绩	8.5	9.1	9.2	8.6	9.3	8.8	9.6	8.9	8.7	9.7
签号	11	12	13	14	15	16	17	18	19
成绩	9.8	9.1	8.9	9.3	9.6	8.8	9	8.7	9.3