云南省昆明市五华区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-07-27 类型:期末考试
一、单选题
-
1. 下列曲线中,表示y是x的函数的是 ( )A、
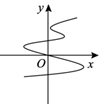 B、
B、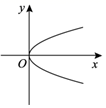 C、
C、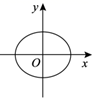 D、
D、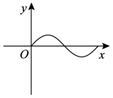 2. 平行四边形具有的特征是( )A、对角线互相平分 B、对角线相等 C、四个角都是直角 D、四边相等3. 下列二次根式中是最简二次根式的是( )A、 B、 C、 D、4. 如图,韩彬同学从家(记作点A)出发向北偏东30°的方向行走了4000米到达超市(记作点B),然后再从超市出发向南偏东60°的方向行走3000米到达卢飞同学家(记作点C),则韩彬家到卢飞家的距离为( )
2. 平行四边形具有的特征是( )A、对角线互相平分 B、对角线相等 C、四个角都是直角 D、四边相等3. 下列二次根式中是最简二次根式的是( )A、 B、 C、 D、4. 如图,韩彬同学从家(记作点A)出发向北偏东30°的方向行走了4000米到达超市(记作点B),然后再从超市出发向南偏东60°的方向行走3000米到达卢飞同学家(记作点C),则韩彬家到卢飞家的距离为( )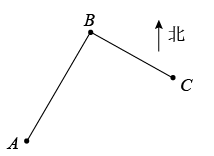 A、5000米 B、6000米 C、7000米 D、8000米5. 一次函数y=kx+b中,y随x的增大而减小,b<0,则这个函数的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,正方体的棱长为2cm,点B为一条棱的中点.蚂蚁在正方体表面爬行,从点A爬到点B的最短路程是( )
A、5000米 B、6000米 C、7000米 D、8000米5. 一次函数y=kx+b中,y随x的增大而减小,b<0,则这个函数的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,正方体的棱长为2cm,点B为一条棱的中点.蚂蚁在正方体表面爬行,从点A爬到点B的最短路程是( )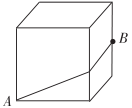 A、 B、 C、 D、7. 实数a,b在数轴上的位置如图所示,则化简的结果是( )
A、 B、 C、 D、7. 实数a,b在数轴上的位置如图所示,则化简的结果是( )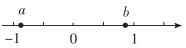 A、 B、 C、 D、08. 将一圆柱形小水杯固定在大圆柱形容器底面中央,现用一个注水管沿大容器内壁匀速注水,如图所示,则小水杯水面的高度与注水时间的函数图象大致是( )
A、 B、 C、 D、08. 将一圆柱形小水杯固定在大圆柱形容器底面中央,现用一个注水管沿大容器内壁匀速注水,如图所示,则小水杯水面的高度与注水时间的函数图象大致是( )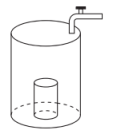 A、
A、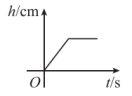 B、
B、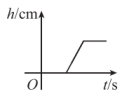 C、
C、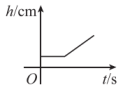 D、
D、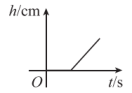 9. 一组从小到大排列的数据:x,3,4,4,5(x为正整数),唯一的众数是4,则该组数据的平均数是( )A、3.6 B、3.2或3.8 C、3.4或3.6 D、3.2或3.610. 如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )
9. 一组从小到大排列的数据:x,3,4,4,5(x为正整数),唯一的众数是4,则该组数据的平均数是( )A、3.6 B、3.2或3.8 C、3.4或3.6 D、3.2或3.610. 如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )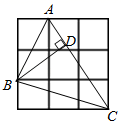 A、 B、 C、 D、11. 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,AE平分 , 分别交BC,BD于点E,P,连接OE,若 , , 则下列结论:① , ② , ③ , ④ . 其中结论正确的有( )
A、 B、 C、 D、11. 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,AE平分 , 分别交BC,BD于点E,P,连接OE,若 , , 则下列结论:① , ② , ③ , ④ . 其中结论正确的有( )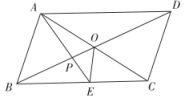 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
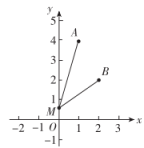
12. 如图,在平面直角坐标系中有两点 , , 点M是y轴上一点,使最小,则点M的坐标为
 13. 使 有意义的x的取值范围是 .14. 《九章算术》是我国最重要的数学著作之一,其中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何”.译文大意是:“有一根竹子高一丈(十尺),竹梢部分折断,尖端落在地上,竹尖与竹根的距离三尺,问竹干还有多高”,若设未折断的竹干长为x尺,根据题意可列方程为 .
13. 使 有意义的x的取值范围是 .14. 《九章算术》是我国最重要的数学著作之一,其中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何”.译文大意是:“有一根竹子高一丈(十尺),竹梢部分折断,尖端落在地上,竹尖与竹根的距离三尺,问竹干还有多高”,若设未折断的竹干长为x尺,根据题意可列方程为 . 15. 农科院助农团队在某地各选6块试验田试种甲、乙两种杂交水稻,收获后统计结果为:千克/亩, , 千克/亩, , 则品种更适合在该地区推广.(填“甲”或“乙”)16. 如图,菱形ABCD中,若 , , 则菱形ABCD的面积为 .
15. 农科院助农团队在某地各选6块试验田试种甲、乙两种杂交水稻,收获后统计结果为:千克/亩, , 千克/亩, , 则品种更适合在该地区推广.(填“甲”或“乙”)16. 如图,菱形ABCD中,若 , , 则菱形ABCD的面积为 .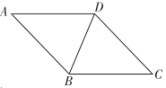 17. 设是x轴正半轴上的一个动点,它与x轴上表示-3的点的距离为y,则y关于x的函数解析式为 .18. 已知点A(0,4),B(7,0),C(7,4),连接AC,BC得到矩形AOBC,点D的边AC上,将边OA沿OD折叠,点A的对应边为 . 若点到矩形较长两对边的距离之比为1:3,则点的坐标为 .
17. 设是x轴正半轴上的一个动点,它与x轴上表示-3的点的距离为y,则y关于x的函数解析式为 .18. 已知点A(0,4),B(7,0),C(7,4),连接AC,BC得到矩形AOBC,点D的边AC上,将边OA沿OD折叠,点A的对应边为 . 若点到矩形较长两对边的距离之比为1:3,则点的坐标为 .三、解答题
-
19. 计算:(1)、;(2)、 .20. 某校为了解家长对昆明市推进爱国卫生“7个专项行动”的知晓情况,通过发放问卷进行测评,从中随机抽取20份答卷,并统计成绩,成绩用x(单位:分)表示.
数据收集:
90
82
99
86
98
96
90
100
89
83
87
88
81
90
93
100
100
96
92
100
数据整理:
3
4
a
4
4
数据分析:
平均分
中位数
众数
92
b
c
请根据以上信息,回答下列问题:
(1)、补全表中数据: , , ;(2)、张凡查到他爸爸考了93分,很自豪的说:“我爸的成绩超过了50%的家长!”张凡的说法对吗?若对,请说明理由;若错,请改正.(3)、该校有1600名家长参加了此次问卷测评活动,请估计成绩不低于90分的人数是多少?21. 在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于种种原因,由C到A的路现在已经不通了,某村为方便村民取水决定在河边新建一个取水点H(A,H,B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.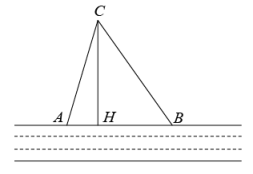 (1)、问CH是不是从村庄C到河边的最近路,请通过计算加以说明;(2)、求原来的路线AC的长.22. 如图,在▱ABCD中,AE⊥BC于点E点,延长BC至F点使CF=BE,连接AF,DE,DF.
(1)、问CH是不是从村庄C到河边的最近路,请通过计算加以说明;(2)、求原来的路线AC的长.22. 如图,在▱ABCD中,AE⊥BC于点E点,延长BC至F点使CF=BE,连接AF,DE,DF.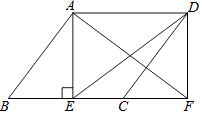 (1)、求证:四边形AEFD是矩形;(2)、若AB=6,DE=8,BF=10,求AE的长.23. 某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)、求证:四边形AEFD是矩形;(2)、若AB=6,DE=8,BF=10,求AE的长.23. 某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)、该网店甲、乙两种羽毛球每筒的售价各是多少元?(2)、根据消费者需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的 ,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案?
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
24. 定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.如图1,∠ABC=∠ADC=90°,四边形ABCD是损矩形,则该损矩形的直径是线段AC . 同时我们还发现损矩形中有公共边的两个三角形角的特点:在公共边的同侧的两个角是相等的.如图1中:△ABC和△ABD有公共边AB , 在AB同侧有∠ADB和∠ACB , 此时∠ADB=∠ACB;再比如△ABC和△BCD有公共边BC , 在CB同侧有∠BAC和∠BDC , 此时∠BAC=∠BDC .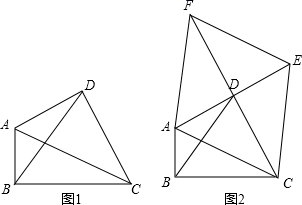 (1)、请在图1中再找出一对这样的角来:= .(2)、如图2,△ABC中,∠ABC=90°,以AC为一边向外作菱形ACEF , D为菱形ACEF对角线的交点,连接BD , 当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由.(3)、在第(2)题的条件下,若此时AB=6,BD=8 ,求BC的长.
(1)、请在图1中再找出一对这样的角来:= .(2)、如图2,△ABC中,∠ABC=90°,以AC为一边向外作菱形ACEF , D为菱形ACEF对角线的交点,连接BD , 当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由.(3)、在第(2)题的条件下,若此时AB=6,BD=8 ,求BC的长.