广东省珠海市香洲区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-07-27 类型：期末考试

进入出卷网下载

一、单选题

1. 下列式子中，属于最简二次根式的是（）

A、 $\sqrt{\frac{1}{3}}$ B、 $\sqrt{3}$ C、 $\sqrt{4}$ D、 $\sqrt{8}$

查看试题解析
2. 在 $△ A B C$ 中， $B C = 8$ ，点D和点E分别为 $A B$ 和 $A C$ 的中点，则 $D E$ 长为（）

A、4 B、5 C、6 D、8

查看试题解析
3. 下列运算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $2 \sqrt{3} - \sqrt{3} = 2$ C、 $2 \sqrt{3} \times 3 \sqrt{3} = 6 \sqrt{3}$ D、 $\sqrt{6} \div \sqrt{2} = \sqrt{3}$

查看试题解析
4. 以下列各组数为边长，能组成直角三角形的是（）

A、1，2，3 B、2，3，4 C、3，4，6 D、1， $\sqrt{3}$ ，2

查看试题解析
5. 菱形 $A B C D$ 的对角线 $A C = 8$ ， $B D = 6$ ，则菱形 $A B C D$ 的面积等于（）

A、12 B、24 C、25 D、48

查看试题解析
6. 如图，直线 $y = x + b$ 与坐标轴交于两点，则 $y > 0$ 时，x的取值范围是（）

A、 $x > 0$ B、 $x < - 2$ C、 $x > - 2$ D、 $x < 1$

查看试题解析
7. 某市规定学生的学期体育成绩满分为60，其中课堂表现占20%，期中成绩占30%，期末成绩占50%．小彤的三项成绩依次为60，50，56，小彤这学期的体育成绩为（）

A、53.5 B、54 C、54.5 D、55

查看试题解析
8. 如图 $△ A B C$ 为直角三角形，斜边 $A C = 4$ ，以两条直角边为直径构成两个半圆，则两个半圆的面积之和为（）

A、 $2 π$ B、 $4 π$ C、 $8 π$ D、 $16 π$

查看试题解析
9. 一养鱼专业户为了估计池塘里有多少条鱼，先捕上100条作上标记，然后放回池塘里．过了一段时间，待标记的鱼混合于鱼群后，再捕捞5次，记录如下：第1次捕捞90条，带标记的有11条；第二次捕捞100条，带标记的有9条；第三次捕捞120条，带标记的有12条：第4次捕捞100条，带标记的有9条；第五次捕捞80条，带标记的有8条．鱼塘内鱼的数量大约为（）

A、900 B、1000 C、1200 D、800

查看试题解析
10. 如图，在平行四边形 $A B C D$ 中， $B E ⊥ C D$ ，垂足E在线段 $C D$ 上通不与点C、D重合，点Q是 $A D$ 的中点，点P由点A出发，沿折线 $A B \to B E \to E C$ 匀速运动，到达点C停止运动，则 $△ A P Q$ 的面积y与点P经过的路程x之间的函数关系的图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 若 $\sqrt{x + 2}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 如图，一个小球由静止开始沿一个斜坡向下滚动，其速度每秒增加 $3 m / s$ ，则小球的速度v（单位： $m / s$ ）关于时间t（单位：s）的函数关系式为．

查看试题解析
13. 直线 $y = 5 x + b$ 不经过第二象限，请写出一个符合条件的b的值．

查看试题解析
14. 若 $x = \sqrt{6} + 1$ ， $y = \sqrt{6} - 1$ ，则 $x^{2} - y^{2} =$ ．

查看试题解析
15. 如图，矩形 $A B C D$ 两条对角线交于点O， $A B = 3$ ，点F在 $B C$ 边上，沿 $D F$ 所在直线折叠矩形，若点C与点O恰好重合，则折痕 $D F$ 的长是．

查看试题解析
16. 四边形 $A B C D$ 中， $A D ∥ B C$ ， $A D$ 与 $B C$ 之间的距离为4， $A B = A D = C D = 5$ ，则边 $B C$ 的长为．

查看试题解析
17. 正方形 $A B C D$ 的边长为2，E是 $B C$ 边上一动点，以 $B E$ 为边向正方形内部作等边 $△ B E F$ ，连接 $D F$ ．当点E从点B开始运动到点C停止运动，线段 $D F$ 扫过的面积为．

查看试题解析

三、解答题

18. 计算： $(\sqrt{6} - 2 \sqrt{3}) \times \sqrt{3} - 12 \times \sqrt{\frac{1}{2}} + \sqrt{18}$

查看试题解析
19. 如图，在平行四边形 $A B C D$ 中，延长边 $C D$ 至F，使得 $C D = D F$ ，连接 $B F$ 交 $A D$ 于点E．求证： $B E = E F$ ．

查看试题解析
20. 《西江月》中描述：平地秋千未起，踏板一尺离地，送行二步恰竿齐，五尺板高离地…；翻译成现代文为：如图，秋千 $O A$ 静止的时候，踏板离地高一尺（ $A C = 1$ 尺）将它往前推进两步（ $E B = 10$ 尺），此时踏板升高离地五尺（ $B D = 5$ 尺），求秋千绳索 $O B$ 的长度．

查看试题解析

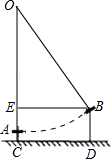21. 某校七、八年级各有200人参加“防新冠安全知识竞赛”，两年级参赛人员中，各随机抽取10名学生的成绩如下：七年级：64 72 86 86 97 64 81 86 91 97

八年级：72 76 79 83 88 89 76 83 83 93

【整理数据】

成绩	$60 \leq x \leq 70$	$70 \leq x \leq 80$	$80 \leq x \leq 90$	$90 \leq x \leq 100$
七年级	2	1	a	3
八年级	0	4	5	1

【分析数据】

统计量	平均数	中位数	众数
七年级	82.4	b	86
八年级	82.2	83	c

【应用数据】

(1)、直接写出

a =

，

b =

，

c =

；

(2)、请结合表格信息，判断样本中（填：七或八）年级学生的竞赛成绩更稳定？

(3)、请估计该校七、八年级成绩大于80分的总人数．

查看试题解析

22. 某饰品店一次性购进“冰墩墩”和“雪容融”共100件进行销售，其中“冰墩墩”的进价为200元/件，售价为300元/件：“雪容融”的进价为100元/件，售价为150元/件．
设购进“冰墩墩”的数量为x（件），销售完这些吉样物的总利润为y（元）．

(1)、请求出y与x之间的函数关系式；

(2)、如果购进的“冰墩墩”的数量不多于“雪容融”的数量的3倍，求购进“冰墩墩”多少件时，这批吉样物销售完利润最多？最多可以获利多少元？

查看试题解析
23. 如图，直线l的表达式为 $y = 2 x - 6$ ，点A，B的坐标分别为 $(1 ， 0)$ ， $(0 ， 2)$ ，直线 $A B$ 与直线l相交于点P．

(1)、若直线 $y = 2 x + m$ 与线段 $A P$ 有交点，求m的取值范围；

(2)、x轴上是否存在点C，使得 $△ B P C$ 是等腰三角形，若存在，求C点坐标；若不存在说明理由．

查看试题解析
24. 如图，正方形 $A B C D$ 中， $A B = 6$ ，点E在 $C D$ 边上运动（不与点C、D重合）．过点B作 $A E$ 的平行线交 $D C$ 的延长线于点F，过点D作 $A E$ 的垂线 $D N$ 分别交于 $A E$ ， $B F$ 于点M、N．

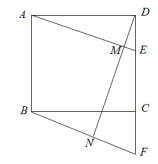(1)、求证：四边形 $A B F E$ 是平行四边形；

(2)、若 $D E = \frac{1}{3} D C$ ，求线段 $M N$ 的长；

(3)、点E在 $C D$ 边上运动过程中， $∠ C N D$ 的大小是否改变？若不变，求出该值，若改变请说明理由．

查看试题解析
25. 宽与长的比是 $\frac{\sqrt{5} - 1}{2}$ （约为0.618）的矩形叫微黄金矩形．它给我们以协调谓匀称的美．
如希腊的帕特农神庙等．下面我们折叠出一个矩形：

第一步，在一张宽为2的矩形纸片一端，用下图的方法折出一个正方形，然后把纸片展平．

第二步，如下图，把这个正方形折成两个相等的矩形，再展平．

第三步，折出内侧矩形的对角线 $A B$ ，并把 $A B$ 折到下图中所示的 $A D$ 处．

第四步，展平纸片，按照所得的点D处折出 $D E$ ，得到矩形 $B C D E$ ．

(1)、证明矩形 $B C D E$ （下图）是黄金矩形．

(2)、定义：直线l将一个面积为S的图形分成面积为 $S_{1}$ 和面积为 $S_{2}$ 的两部分（设 $S_{1} < S_{2}$ ），如果 $\frac{S_{1}}{S_{2}} = \frac{S_{2}}{S}$ ，那么称直线l为该图形的“黄金分割线”．证明：直线 $B C$ 是矩形 $M N D E$ 的黄金分割线；

(3)、下图中，以C为原点， $C D$ 、 $C B$ 所在直线为坐标轴建立平面直角坐标系，直接写出 $△ E N D$ 中经过点C的“黄金分割线”的解析式．（不要求写过程）

查看试题解析