广东省阳江市阳东区2021-2022学年八年级下学期期末考试数学试题
试卷更新日期:2022-07-27 类型:期末考试
一、单选题
-
1. 下列式子中,表示y是x的正比例函数的是( )A、 B、 C、 D、2. 对一组数据: , 1,2,1,下列说法错误的是( )A、平均数是1 B、众数是1 C、中位数是1 D、方差是2.253. 下列各组二次根式中,化简后是同类二次根式的是( )A、 与 B、 与 C、 与 D、 与4. 如图,四边形ABCD为菱形,A , B两点的坐标分别是(2,0),(0,1),点C , D在坐标轴上,则菱形ABCD的周长等于( )
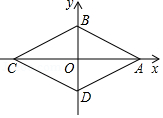 A、 B、4 C、4 D、205. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,D,E,F分别为AB,AC,AD的中点,若BC=2,则EF的长度为( )
A、 B、4 C、4 D、205. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,D,E,F分别为AB,AC,AD的中点,若BC=2,则EF的长度为( )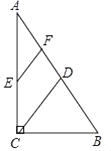 A、 B、1 C、 D、6. 如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( )
A、 B、1 C、 D、6. 如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( ) A、90° B、60° C、45° D、30°7. 如图,在△ABC中,点D,E,F分别是AB,BC,AC的中点,连接DE,EF,DF,则下列说法错误的是( )
A、90° B、60° C、45° D、30°7. 如图,在△ABC中,点D,E,F分别是AB,BC,AC的中点,连接DE,EF,DF,则下列说法错误的是( )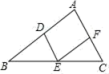 A、S△DEF=S△ABC B、△DEF≌△FAD≌△EDB≌△CFE C、四边形ADEF,四边形DBEF,四边形DECF都是平行四边形 D、四边形ADEF的周长=四边形DBEF的周长=四边形DECF的周长8. 园林队在某公园进行绿化,中间休息了一段时间.已知绿化面积s(单位:平方米)与工作时间t(单位:小时)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为( )
A、S△DEF=S△ABC B、△DEF≌△FAD≌△EDB≌△CFE C、四边形ADEF,四边形DBEF,四边形DECF都是平行四边形 D、四边形ADEF的周长=四边形DBEF的周长=四边形DECF的周长8. 园林队在某公园进行绿化,中间休息了一段时间.已知绿化面积s(单位:平方米)与工作时间t(单位:小时)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为( ) A、40平方米 B、50平方米 C、80平方米 D、100平方米9. 已知一次函数y=x+a与y=﹣x+b的图象都经过点A(﹣2,0),且与y轴分别交于B,C两点,那么△ABC的面积是( )A、2 B、3 C、4 D、510. 如图,菱形ABCD的对角线AC,BD交于点 ,将 沿点 到点 的方向平移,得到 ,当点 与点 重合时,点 与点 之间的距离为( )
A、40平方米 B、50平方米 C、80平方米 D、100平方米9. 已知一次函数y=x+a与y=﹣x+b的图象都经过点A(﹣2,0),且与y轴分别交于B,C两点,那么△ABC的面积是( )A、2 B、3 C、4 D、510. 如图,菱形ABCD的对角线AC,BD交于点 ,将 沿点 到点 的方向平移,得到 ,当点 与点 重合时,点 与点 之间的距离为( )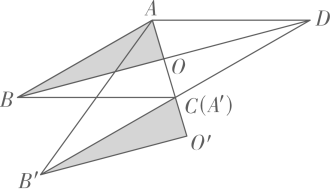 A、6 B、8 C、10 D、12
A、6 B、8 C、10 D、12二、填空题
-
11. 在环保整治行动中,某市环保局对辖区内的单位进行了抽样调查,他们的综合得分如下:95,85,83,95,92,90,96,则这组数据的中位数是 , 众数是 .12. 将直线向上平移5个单位,得到一个一次函数的图象,那么这个一次函数的解析式是 .13. 甲、乙两位同学在近五次数学测试中,平均成绩均为90分,方差分别为 ,甲、乙两位同学成绩较稳定的是同学.14. 当直线 经过第二、三、四象限时,则 的取值范围是 .15. 如图,在平面直角坐标系中,菱形OABC的一个顶点在原点O处,且∠AOC=60°,A点的坐标是(0,4),则直线AC的表达式是 .
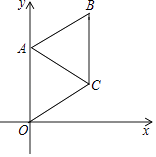 16. 如图所示的网格是正方形网格,则 =°(点A,B,P是网格线交点).
16. 如图所示的网格是正方形网格,则 =°(点A,B,P是网格线交点).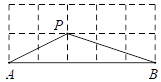 17. 如图,折叠矩形纸片 , 使点B落在点D处,折痕为 , 已知 , 求的长是 .
17. 如图,折叠矩形纸片 , 使点B落在点D处,折痕为 , 已知 , 求的长是 .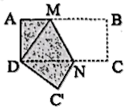
三、解答题
-
18. 计算:19. 如图,在平行四边形中,对角线 , 相交于点O,分别过点A,C作 , , 垂足分别为E,F,求证: .
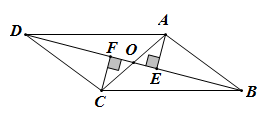 20. 如图,在平面直角坐标系中,过点的直线与直线相交于点 , 求直线的解析式.
20. 如图,在平面直角坐标系中,过点的直线与直线相交于点 , 求直线的解析式.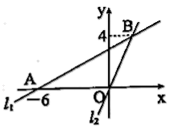 21. 如图,将▱ABCD的边DC延长至点E,使 , 连结AE,交BC于点F.
21. 如图,将▱ABCD的边DC延长至点E,使 , 连结AE,交BC于点F.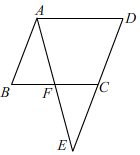 (1)、求证:≌;(2)、连结AC,BE,若四边形ABEC是菱形,且 , , 求AD的长度.22. 如图:每个小正方形的边长都是1.
(1)、求证:≌;(2)、连结AC,BE,若四边形ABEC是菱形,且 , , 求AD的长度.22. 如图:每个小正方形的边长都是1. (1)、求四边形的周长.(2)、求证:.23. 某医药研究所开发了一种新药,在试验药效时发现:如朵成人按规定服用,服药后2小时血液中含药量最高,达每毫升6微克,接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药征y(微克)随时间x(小时)的变化如图所示.
(1)、求四边形的周长.(2)、求证:.23. 某医药研究所开发了一种新药,在试验药效时发现:如朵成人按规定服用,服药后2小时血液中含药量最高,达每毫升6微克,接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药征y(微克)随时间x(小时)的变化如图所示.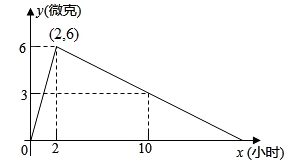 (1)、分别求出和时,y与x之间的函数解析式;(2)、如果每毫升血液中含药量为4微克或4微克以上时在治疗疾病时有效,那么这个有效时间多长?24. 为庆祝中国共产党建党100周年,某校举行了“红色华诞,党旗飘扬”党史知识竞赛,为了解竞赛成绩,抽样调查了七、八年级部分学生的分数,过程如下:
(1)、分别求出和时,y与x之间的函数解析式;(2)、如果每毫升血液中含药量为4微克或4微克以上时在治疗疾病时有效,那么这个有效时间多长?24. 为庆祝中国共产党建党100周年,某校举行了“红色华诞,党旗飘扬”党史知识竞赛,为了解竞赛成绩,抽样调查了七、八年级部分学生的分数,过程如下:收集数据:
从该校七、八年级学生中各随机抽取20名学生的分数,其中被抽取的20名八年级学生的分数如下:
81 83 84 85 86 87 87 88 89 90
92 92 93 95 95 95 99 99 100 100
整理、描述数据:
按下表分段整理、描述样本数据:
七年级
4
6
2
8
八年级
3
a
4
7
分析数据:
两组样本数据的平均数、中位数、众数、方差如表所示:
年级
平均数
中位数
众数
方差
七年级
91
89
97
40.9
八年级
91
b
c
d
根据以上提供的信息,解答下列问题:
(1)、填空:a= , b= , c= , d=;(2)、样本数据中,七年级甲同学和八年级乙同学的分数都为90分,同学的分数在本年级抽取的分数中从高到低排序更靠前(填“甲”或“乙”),请说明理由;(3)、如果七年级共有400人参赛,求该年级约有多少人的分数不低于95分.25. 如图,把矩形纸片OABC放入平面直角坐标系中,使OA,OC分别落在x轴、y轴的正半轴上,连接AC,且 , .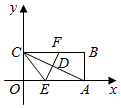 (1)、求点A,C的坐标;(2)、将矩形纸片OABC折叠,使点A与点C重合(折痕为EF),求折叠后纸片重叠部分 的面积.(3)、求EF所在直线的函数解析式.
(1)、求点A,C的坐标;(2)、将矩形纸片OABC折叠,使点A与点C重合(折痕为EF),求折叠后纸片重叠部分 的面积.(3)、求EF所在直线的函数解析式.