广东省阳江市江城区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-07-27 类型：期末考试

进入出卷网下载

一、单选题

1. 二次根式 $\sqrt{x + 3}$ 中的x取值范围是（）

A、 $x \geq - 3$ B、 $x \geq 3$ C、 $x \geq 0$ D、 $x > - 3$

查看试题解析
2. 一组数据：5，6，5，3，7的众数是（）

A、3 B、5 C、6 D、7

查看试题解析
3. 下列计算正确的是（　　）

A、2 $\sqrt{3}$ +4 $\sqrt{2}$ ＝6 $\sqrt{5}$ B、 $\sqrt{5}$ ﹣ $\sqrt{2}$ ＝ $\sqrt{3}$ C、 $\sqrt{27}$ ÷ $\sqrt{3}$ ＝9 D、﹣（ $\sqrt{2}$ ）²＝﹣2

查看试题解析
4. 关于函数 $y = \frac{1}{6} x$ ，下列结论中，正确的是（）

A、函数图象经过点 $(1 ， 6)$ B、不论x为何值，总有 $y > 0$ C、y随x的增大而减小 D、函数图象经过一、三象限

查看试题解析
5. 6位参加百米决赛的同学的成绩各不相同，按成绩取前3位设奖.如果小刘知道了自己的成绩后，要判断能否获奖，需知道其他5位同学成绩的（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
6. 如图，四边形ABCD的对角线AC，BD交于点O，则不能判断四边形ABCD是平行四边形的是（）

A、∠ABD=∠BDC，OA=OC B、∠ABC=∠ADC，AD∥BC C、∠ABC=∠ADC，AB=CD D、∠ABD=∠BDC，∠BAD=∠DCB

查看试题解析
7. 已知关于x的一次函数y＝kx＋2k－3的图象经过原点，则k的值为（）

A、0 B、 $\frac{3}{2}$ C、 $\frac{2}{3}$ D、3

查看试题解析
8. 如图，平地上A、B两点被池塘隔开，测量员在岸边选一点C，并分别找到AC和BC的中点M、N，测量得MN＝8米，则A、B两点间的距离为（　　）

A、4米 B、24米 C、16米 D、48米

查看试题解析
9. 某商场销售A ， B ， C ， D四种商品，它们的单价依次是50元，30元，20元，10元．某天这四种商品销售数量的百分比如图所示，则这天销售的四种商品的平均单价是（）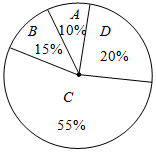

A、19.5元 B、21.5元 C、22.5元 D、27.5元

查看试题解析
10. 如图所示，一次函数 $y = a x + b$ 与 $y = c x + d$ 的图象如图所示，下列说法：
①对于函数 $y = - a x + b$ 来说，y随x的增大而增大；②函数 $y = a x + d$ 不经过第四象限；
③不等式 $a x - d \geq c x - b$ 的解集是 $x \geq 4$ ；④ $4 (a - c) = d - b$ ．
其中正确的是（）

A、2个 B、1个 C、3个 D、4个

查看试题解析

二、填空题

11. 化为最简二次根式 $\sqrt{24} =$ ．

查看试题解析
12. 在平行四边形ABCD中，若∠B+∠D＝160°，∠C＝°.

查看试题解析
13. 一次函数 $y = 2 x + 1$ 的图像向下平移2个单位，得到新的一次函数表达式是．

查看试题解析
14. 甲、乙两名篮球运动员进行每组10次的投篮训练，5组投篮结束后，两人的平均命中数都是7次，方差分别是S_甲²＝1.4，S_乙²＝0.85，则在本次训练中，运动员　　的成绩更稳定．

查看试题解析
15. 如图，网格中每个小正方形的边长均为1，以A为圆心，AB为半径画弧，交最上方的网格线于点D，则ED的长是．

查看试题解析
16. 如图，直线y＝﹣2x+2与x轴交于点A，与y轴交于点B．若点P为x轴上一点，且△ABP的面积为3，则点P的坐标为．

查看试题解析
17. 如图，∠MON＝90°，矩形ABCD的顶点A、B分别在边OM、ON上，当B在边ON上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB＝6，BC＝2．运动过程中点D到点O的最大距离是．

查看试题解析

三、解答题

18. 计算： $\frac{1}{\sqrt{3}} + 2 \sqrt{12} - \sqrt{27}$ ．

查看试题解析
19. 如图，直线l是一次函数y＝kx+b的图象．

(1)、求出这个一次函数的解析式．

(2)、根据函数图象，直接写出y＜2时x的取值范围．

查看试题解析
20. 如图，在△ABC中，AE＝3，BE＝5，AC＝4，DE是BC的垂直平分线，交BC于点D，交AB于点E．求证：△ABC为直角三角形．

查看试题解析
21. 某中学为了解初三学生参加志愿者活动的次数，随机调查了该年级20名学生，统计得到该20名学生参加志愿者活动的次数如下：3；5；3；6；3；4；4；5；2；4；5；6；1；3；5；5；4；4；2；4
根据以上数据，得到如下不完整的频数分布表：

次数

1

2

3

4

5

6

人数

1

2

a

6

b

2

(1)、表格中的 $a =$ ， $b =$ ；

(2)、在这次调查中，参加志愿者活动的次数的众数为，中位数为；

(3)、若该校初三年级共有300名学生，根据调查统计结果，估计该校初三年级学生参加志愿者活动的次数为4次的人数．

查看试题解析
22. 如图，在平行四边形ABCD中，E，F为AB边上的两点，且AE＝BF，DF＝CE．求证：

(1)、△ADF≌△BCE．

(2)、平行四边形ABCD是矩形．

查看试题解析
23. 冰墩墩（BingDwenDwen），是2022年北京冬季奥运会的吉祥物．将熊猫形象与富有超能量的冰晶外壳相结合，头部外壳造型取自冰雪运动头盔，装饰彩色光环，整体形象酷似航天员．冬奥会来临之际，冰墩墩玩偶非常畅销．小冬在某网店选中A，B两款冰墩墩玩偶，决定从该网店进货并销售．两款玩偶的进货价和销售价如表：

A款玩偶
B款玩偶
进货价（元/个）
20
15
销售价（元/个）
28
20

(1)、第一次小冬用550元购进了A，B两款玩偶共30个，求两款玩偶各购进多少个．

(2)、第二次小冬进货时，网店规定A款玩偶进货数量不得超过B款玩偶进货数量的一半．小冬计划购进两款玩偶共45个，应如何设计进货方案才能获得最大利润，最大利润是多少？

查看试题解析
24. 定义：对于平面直角坐标系xOy中的点 $P (0 ， k)$ 和直线 $y = k x$ ，我们称点 $P (0 ， k)$ 是直线 $y = k x$ 的反关联点，直线 $y = k x$ 是点 $P (0 ， k)$ 的反关联直线．特别地，当 $k = 0$ 时，直线 $y = 0$ 的反关联点为 $P (0 ， 0)$ ．已知点 $A (- 2 ， 2)$ ， $B (0 ， - 4)$ ， $C (0 ， 0)$ ．

(1)、点B的反关联直线的解析式为，直线AC的反关联点的坐标为；

(2)、设直线AC的反关联点为点D；
①若点P在直线AC上，求 $P B + P D$ 的最小值；
②若点E在点B的反关联直线上，且 $S_{△ B D E} = 4$ ，求点E的坐标．

查看试题解析
25.

(1)、正方形ABCD，E、F分别在边BC、CD上（不与端点重合），∠EAF＝45°，EF与AC交于点G
①如图（i），若AC平分∠EAF，直接写出线段EF，BE，DF之间等量关系；
②如图（ⅱ），若AC不平分∠EAF，①中线段EF，BE，DF之间等量关系还成立吗？若成立请证明；若不成立请说明理由

(2)、如图（ⅲ），矩形ABCD，AB＝4，AD＝8．点M、N分别在边CD、BC上，AN＝2 $\sqrt{5}$ ， ∠MAN＝45°，求AM的长度．

查看试题解析

	A款玩偶	B款玩偶
进货价（元/个）	20	15
销售价（元/个）	28	20

次数	1	2	3	4	5	6
人数	1	2	a	6	b	2